Hyperbola

Hva er en hyperbola?

Hyperbolaen er settet med punktene i planet slik at den absolutte verdien av forskjellen mellom avstandene til to faste punkter, kalt søkelys, forblir konstant. Dette settet med punkter danner kurven med to grener observert i figur 1.

Det er et punkt p (x, y), foci f₁ og f₂ separert en avstand lik 2C. Den matematiske måten å uttrykke dette forholdet på er gjennom:

Figur 1. Hyperbola med horisontal fokalaks. Kilde: f. Zapata.

Alle punktene i hyperbola tilfredsstiller denne tilstanden, noe som fører til hyperbola -ligningen, som det vil bli sett senere. Midtpunktet mellom søkelysene kalles sentrum C og i figuren sammenfaller det med punktet (0,0), men hyperbolaen kan også forskyves og dets sentrum tilsvarer et annet koordinatpunkt C (H, K).

I den øvre figuren er x -aksen den fokale aksen til hyperbola, siden det er søkelysene, men du kan også bygge en hvis fokalaks er aksen og aksen.

Hyperbolaen er en del av kurvene kjent som konisk, De kalles det fordi de kan avledes fra kuttet av en kjegle med en flat seksjon. En hyperbola oppnås når du krysser kjeglen og flyet, forutsatt at den ikke passerer gjennom toppunktet til kjeglen og vinkelen som danner planet med keglenes akse er mindre enn den som dannes med generatrix -aksen til den samme.

Sammen med lignelsen, omkretsen og ellipsen er CONICS kjent siden eldgamle tider. Den greske matematikeren Apollonius fra Perga (262-190 f.Kr.) skrev en geometri-traktat der han detaljerte egenskapene sine, og han ga dem selv navnene de kjenner hverandre til i dag.

Kjennetegn på hyperbolaen

Dette er noen av de mest fremragende egenskapene til en hyperbola:

1. Det er en flat kurve, derfor er det nok å gi koordinatene (x, y) for hvert punkt som tilhører den.
2. Det er også en åpen kurve, i motsetning til omkretsen eller ellipsen.
3. Den har to grener arrangert symmetrisk.
4. Både den vertikale aksen og den horisontale aksen kan betraktes som symmetriakser, men aksen der søkelysene kalles fokalakse eller hovedakse.
5. Det er symmetrisk med hensyn til sentrum.
6. Hyperbolaen krysser fokalaksen på to punkter som kalles Hjørner, Det er grunnen til at fokalaksen noen ganger kalles ekte akse, mens den andre aksen kalles Imaginær akse, Fordi det ikke har noen poeng til felles med hyperbolaen.
7. Sentrum av hyperbolaen ligger halvveis mellom punktene som kalles foci.
8. Det er assosiert med to veldig spesielle linjer kalt asymptoter, som er linjer som hyperbolaen nærmer seg, men uten å krysse dem, når verdiene til x e y er veldig store. Asymptotene krysser hverandre i midten av hyperbolaen.

Kan tjene deg: Overjektive funksjon: Definisjon, egenskaper, eksempler

Ligninger og formler

Hiperbol -ligning med sentrum i (0,0)

Starter fra definisjonen gitt i begynnelsen:

Til denne positive konstanten kalles det vanligvis 2A, og det er avstanden som skiller toppunktene til hyperbola, da:

På den annen side, DP₁, DP₂ og 2C er sidene av trekanten vist i figur 1, og ved elementær geometri er subtraksjonen av rutene på sidene av en hvilken som helst trekant alltid mindre enn kvadratet på den gjenværende siden. Så:

4. plass² < 4c²

OG:

til < c

Dette resultatet vil være nyttig snart.

Som avstanden mellom to punkter p₁(x₁,og₁) Og s₂(x₂,og₂) er:

Ved å erstatte koordinater P (x, y), f₁(-C, 0) og f₂(C, 0) Det gjenstår:

Som tilsvarer:

Firkantet i begge medlemmene for å eliminere røttene og omorganisere vilkårene du når:

Til mengde c² - til², som alltid er en positiv mengde fordi < c, se la denomina b², Derfor blir ovennevnte skrevet om som:

b²x² - til²og² = a² b²

Dele alle vilkår med² b², Det er Hyperbola -ligningen sentrert på (0,0) med den horisontale reelle aksen:

Med A og B større enn 0. Denne ligningen kalles Hyerbola kanonisk ligning og nevneren til² Det tilsvarer alltid den positive brøkdelen.

Hyperbola sentrerte seg om (0,0) og med den virkelige aksen har vertikal formen:

Kryss av hyperbolaen med koordinataksene

Kryssene mellom hyperbola med koordinataksene blir gjort henholdsvis y = 0 og x = 0 i ligningen:

For y = 0

x² /til² = 1 ⇒ x² = a²

x = ± a

Hyperbolaen skjærer til x -aksen i to punkter kalt hjørner, hvis respektive koordinater x er: x = a y x = -a

For x = 0

Det er oppnådd -og² /b² = 1, som ikke har noen reell løsning og følger at hyperbolaen ikke kutter seg til den vertikale aksen.

Hyperbola ligning med sentrum i (h, k)

Hvis sentrum av hyperbola er på punkt C (h, k), er dens kanoniske ligning:

Hiperbola -elementer

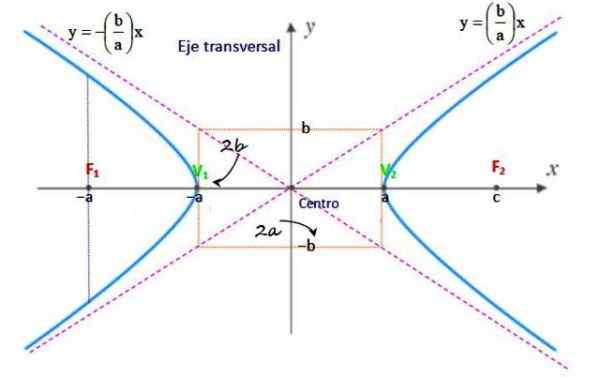Figur 2. Hiperbola -elementer. Kilde: f. Zapata.

Senter

Det er midtpunktet i segment f₁F₂ Og koordinatene er (h, k) eller (x_enten,og_enten).

Kan tjene deg: syntetisk divisjon

Focos

De er de to faste punktene f₁ og f₂ som er på den virkelige aksen til hyperbolaen, med hensyn til hvilken forskjellen på avstander til punkt p (x, y) forblir konstant. Avstanden mellom søkelysene og midten av hyperbolaen er "C".

Vektorradio

Dette kalles avstanden mellom et punkt P og en av søkelysene.

Fokalavstand

Det er avstanden som skiller både søkelys og tilsvarer 2C.

Hjørner

Toppunktene v₁ og v₂ De er punktene der hyperbolaen krysser den virkelige aksen. Et toppunkt og sentrum av hyperbolaen skilles med avstand A, derfor er avstanden mellom toppunktene 2A.

Fokal akse, hovedakse eller ekte akse

Det er aksen der søkelysene er lokalisert og måler 2C. Det kan være plassert på en av de to kartesiske aksene, og hyperbolaen krysser den på punktene som kalles toppunkter.

Tverrgående akse, sekundær akse eller imaginær akse

Det er aksen vinkelrett på fokalaksen og måler 2b. Hyperbolaen krysser den ikke, så den kalles også en imaginær akse.

Asymptoter

De er to linjer, hvis respektive verserende er m₁ = (b/a) og m₂ = - (b/a), som er ment i sentrum av hyperbolaen. Kurven krysser aldri disse linjene og produktet mellom avstandene til et hvilket som helst punkt i hyperbola til asymptotene, det er konstant.

For å finne ligningene til asymptotene, samsvarer bare med venstre side av Hyperbola kanonisk ligning til 0. For eksempel for hyperbola sentrert om opprinnelse:

Hyberbola rektangel

Det er rektangelet hvis bredde er avstanden mellom toppunktene 2a og avstand 2B og er fokusert på midten av hyperbolaen. Konstruksjonen letter den manuelle utformingen av hyperbolaen.

Rett side

Tau som går gjennom en av søkelysene, vinkelrett på den virkelige aksen.

Eksentrisitet

Det er definert som kvotienten mellom brennavstanden og den virkelige aksen:

E = C/A

Det er alltid større enn 1, siden C er større enn A, og mindre enn √2.

Verdien av og indikerer om hyperbolaen er ganske lukket (smalt rektangel, langstrakt i retning av hovedaksen) eller åpen (bredt rektangel, langstrakt i retning av den imaginære aksen).

Rett tangent til hyperbola på punkt P (x₁,og₁)

En tangentlinje til hyperbola på et punkt P (x₁,og₁) Det er bisektoren til de to radiovektorene til det punktet.

For en hyperbola med hovedaksen parallelt med x -aksen, skråningen av linjen tangens til hyperbola på et punkt P (x₁,og₁) er gitt av:

Kan tjene deg: kombinert operasjoner

Og hvis hyperbolaen er hovedaksen parallelt med Y -aksen, så:

Eksempler på hyperbola

Spredning av alfa -partikler av en kjerne

Ved å bombardere atomkjerner med alfa -partikler, som ikke er annet enn heliumkjerner, blir disse frastøtt, siden enhver atomkjerne har en positiv ladning. Disse heliumkjernene er spredt etter hyperbolske baner.

Bane for solsystemorganene

Figur 3: Solsystemplaneter

I solsystemet beveger gjenstander seg under virkningen av tyngdekraften. Beskrivelsen av bevegelsen stammer fra en differensialligning der styrken er konservativ og omvendt proporsjonal med kvadratet på avstanden. Og løsningene på denne ligningen er de mulige banene som følger objektene.

Vel, disse banene er alltid koniske: omkretser, ellipser, lignelser eller hyperbolas. De to første er lukkede kurver, og det er slik planetene beveger seg, men noen kometer er fremdeles åpne bane, for eksempel lignelser eller hyperbolas, med solen plassert i en av søkelysene.

Minimum lyd

Når det er to lydkilder, for eksempel to høyttalere som avgir lyder jevnt i alle retninger, som ligger langs en rett linje, er minimumene av lydintensitet (destruktiv interferens) på en hyperbola hvis hovedakse er sagt linje, og i søkelysene i Hyperbola er høyttalerne.

Trening løst

Finn elementene i følgende hyperbola: hjørner, foci og asymptoter av hyperbola og bygg grafen:

Løsning

Senteret av denne hyperbola sammenfaller med opprinnelsen til koordinatene og dens virkelige akse er horisontalt, siden den positive fraksjonen tilsvarer variabel x.

Hyperbola semi -aksene er:

til² = 16 ⇒ a = 4

b² = 4 ⇒ B = 2

På denne måten måler det sentrale rektangelet 4 enheter brede og 2 enheter høye. Husker at det ble nevnt ovenfor at C² - til² = b² , så:

c² = a² + b² ⇒ c² = 16 + 4 = 20

Derfor er fokal semi-duty:

C = √20 = 2√5

Og fokusene er på koordinatpunkter f₁ (-2√5.0) og f₂ (2√5.0).

Bakkene til asymptotene er:

m = ± (b/a) = ± (2/4) = ± 0.5

Derfor er de respektive ligningene for hver enkelt:

og₁ = 0.5x; og₂ = -0.5x

Hyperbola kan enkelt tegne gjennom online programvare som Geogebra:

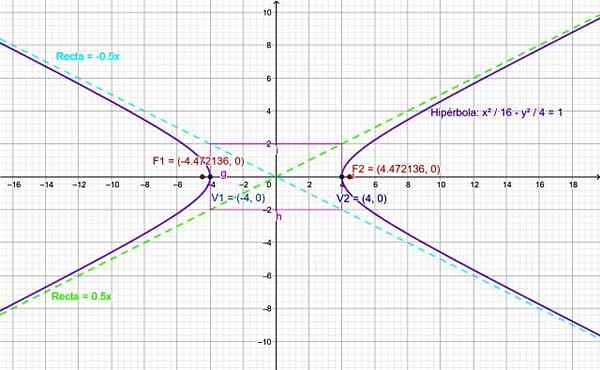Figur 4. Graf for hyperbola på øvelsen løst. Kilde: f. Zapata.

Referanser

1. Fisicalab. Hyperbola -ligning. Gjenopprettet fra: Fisicalab.com
2. Hoffman, J. Valg av matematikkproblemer. Volum 2.
3. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
4. Universformler. Hyperbola. Gjenopprettet fra: Universoformulas.com
5. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.