Homotecia

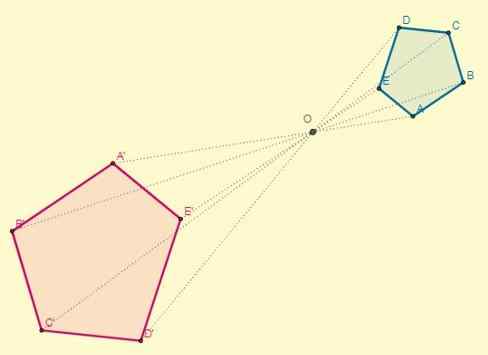
De Homotecia Det er en geometrisk endring i flyet der, fra et fast punkt kalt sentrum (O), avstander multipliseres med en felles faktor. På denne måten tilsvarer hvert punkt P et annet punkt i transformasjonen, og disse er på linje med punktet eller.

Deretter er homotecia en korrespondanse mellom to geometriske figurer, der de transformerte punktene kalles homotetisk, og disse er på linje med et fast punkt og med parallelle segmenter med hverandre.

Forklaring og formel

Homotecia er en transformasjon som ikke har et kongruent bilde, fordi de fra en figur vil få en eller flere figurer av større eller mindre størrelse enn den opprinnelige figuren; det vil si at homotecia forvandler en polygon til en annen lignende.

For at Homotecia skal oppfylles, må punkt til punkt og rett linje korrespondere, slik at par av homologe prikker er på linje med et tredje fast punkt, som er sentrum for homotecia.

På samme måte skal parene som forenes være parallelle. Forholdet mellom slike segmenter er en konstant kalt homotecia (k) grunn; På en slik måte at homotecia kan defineres som:

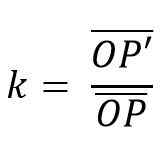
For å gjøre denne typen transformasjoner begynner et vilkårlig punkt, som vil være sentrum for homotecia.

Fra dette punktet trekkes linjesegmenter for hvert toppunkt for figuren som skal transformeres. Skalaen som reproduksjonen av den nye figuren er gitt på, er gitt av grunnen til homotecia (k).

Homotecia egenskaper

En av hovedegenskapene til homotecia er at alle homotiske figurer av grunnen til homotecia (k) er like. Blant andre fremragende egenskaper er følgende:

Det kan tjene deg: sammensatt proporsjonalitet: forklaring, tre sammensatte regel, øvelser

- Homotecia Center (O) er det eneste dobbeltpunktet, og det forvandler seg; det vil si at det ikke varierer.

- Linjene som passerer gjennom sentrum blir seg selv (de er doble), men punktene som utgjør det er ikke doble.

- Linjene som ikke passerer gjennom sentrum, blir omgjort til parallelle linjer; På denne måten forblir homotecia -vinklene like.

- Bildet av et segment av et sentrum homotecia eller og grunn k, er et segment parallelt med det og har k ganger sin lengde. Som for eksempel sett i følgende bilde, vil et AB -segment for homotecia være et annet A'B -segment ', slik at AB vil være parallell med a'b' og k vil være:

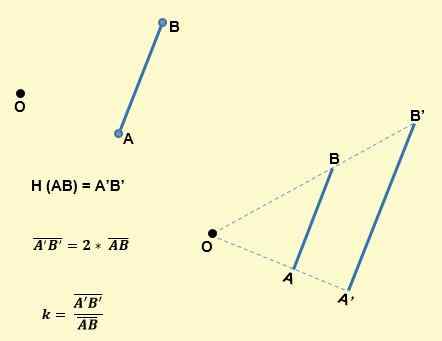
- Homotetiske vinkler er kongruente; det vil si at de har samme tiltak. Derfor er bildet av en vinkel en vinkel som har samme amplitude.

På den annen side må homotecia varieres avhengig av verdien av sin grunn (k), og følgende tilfeller kan oppstå:

- Hvis konstant k = 1, er alle punktene fikset fordi de transformerer seg. Dermed sammenfaller den homotetiske figuren med originalen, og transformasjonen vil bli kalt identitetsfunksjon.

- Hvis k ≠ 1, vil det eneste faste punktet være sentrum for homotecia (O).

- Hvis k = -1, blir homotecia en sentral symmetri (c); Det vil si at en rotasjon vil skje rundt C, i en vinkel på 180^enten.

- Hvis k> 1, vil størrelsen på den transformerte figuren være større til størrelsen på originalen.

Kan tjene deg: irrasjonelle tall: historie, egenskaper, klassifisering, eksempler

- Ja 0 < k < 1, el tamaño de la figura transformada será menor que el de la original.

- Ja -1 < k < 0, el tamaño de la figura transformada será menor y estará girada con respecto a la original.

- Ja k < -1, el tamaño de la figura transformada será mayor y estará girada con respecto a la original.

Typer homotecia

Homotecia kan også klassifiseres i to typer, avhengig av verdien av sin grunn (k):

Direkte homotecia

Oppstår hvis konstant k> 0; Det vil si at homotetiske punkter er på samme side med hensyn til sentrum:

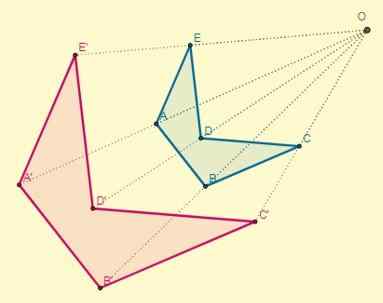
Proporsjonalitetsfaktoren eller likhetsforholdet mellom direkte homotetiske figurer vil alltid være positiv.

Inverse Homotecia

Oppstår hvis konstant k < 0; es decir, los puntos iniciales y sus homotéticos se ubican en los extremos opuestos con respecto al centro de la homotecia pero alineados a esta. El centro se encontrará entre las dos figuras:

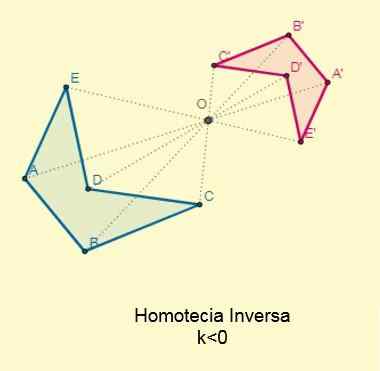
Proporsjonalitetsfaktoren eller likhetsforholdet mellom de omvendte homotetiske figurene vil alltid være negativ.

Sammensetning

Når flere bevegelser blir utført suksessivt til et figur som er lik originalen, oppstår en sammensetning av bevegelser. Sammensetningen av flere bevegelser er også en bevegelse.

Sammensetningen mellom to homotecia resulterer i en ny homotecia; Det vil si at det er et homotecia -produkt der senteret vil være på linje med sentrum av de to originale transformasjonene, og grunnen (k) er produktet av de to grunnene.

Dermed i sammensetningen av to homotier h₁(ENTEN₁, k₁) og h₂(ENTEN₂, k₂), Multiplikasjonen av årsakene dine: k₁ x k₂ = 1 vil resultere i en homotecia av grunn k₃ = K₁ x k₂. Sentrum av denne nye homotecia (eller₃) vil være lokalisert på linjen eller₁ ENTEN₂.

Det kan tjene deg: motsatte vinkler med toppunktet (med en løst øvelse)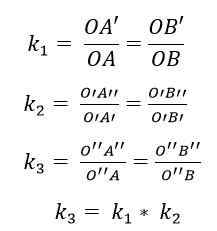

Homotecia tilsvarer en flat og irreversibel forandring; Hvis to homotecia gjelder som har samme senter og fornuft, men med et annet tegn, vil det originale figuren oppnås.

Homotecia eksempler

1. Første eksempel

Bruk en homotecia på den gitte polygonen til sentrum (O), lokalisert 5 cm fra punkt A og hvis grunn er k = 0,7.

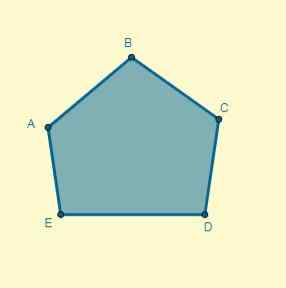
Løsning

Ethvert punkt er valgt som sentrum for homotecia, og fra dette blir de trukket ut av toppunktene til figuren:

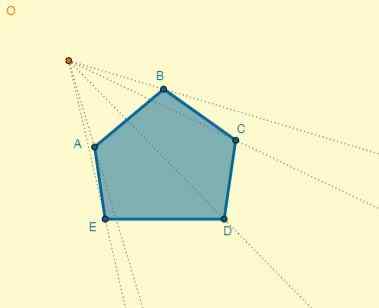
Avstanden fra sentrum (O) til punktet A er OA = 5; Med dette kan du bestemme avstanden til et av de homotetiske punktene (OA ') også vite at K = 0,7:

Oa '= k x oa.

OA '= 0,7 x 5 = 3,5.

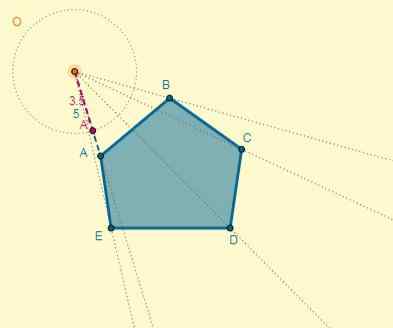
Prosessen kan gjøres for hvert toppunkt, eller du kan også tegne den homotetiske polygonen som husker at de to polygonene har parallelle sider:

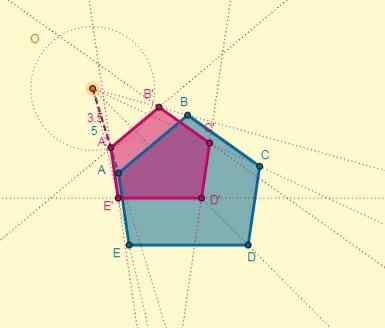
Til slutt blir transformasjonen sett på som følger:

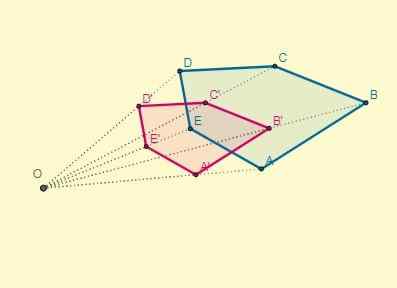
2. Andre eksempel

Påfør en homotecia på den gitte polygonen til sentrum (O), som ligger 8,5 cm fra punkt C og hvis og grunn k = -2.

Løsning

Avstanden fra sentrum (O) til punkt C er OC = 8,5; Med disse dataene er det mulig å bestemme avstanden til et av de homotetiske punktene (OC '), og også vite at K = -2:

Oc '= k x oc.

Oc '= -2 x 8,5 = -17

Etter å ha tegnet segmentene av toppunktene til den transformerte polygonen, er de opprinnelige punktene og deres homotetikk lokalisert i motsatte ender med hensyn til sentrum: