Matematisk likhet

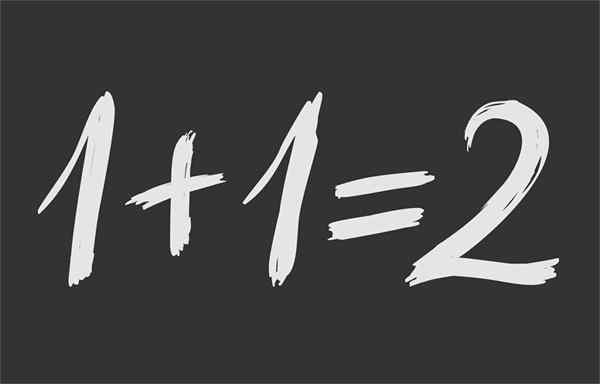Figur 1.- Matematisk likhet sikrer at 1 + 1 er den samme 2

Hva er matematisk likhet?

En matematisk likhet sikrer at to uttrykk er de samme eller forskjellige, de er helt likeverdige. Disse uttrykkene kan være mangfoldig natur, for eksempel tall, bokstaver som symboliserer mengder eller størrelser, kombinasjoner av tall og bokstaver, matriser og mer.

Symbolet som brukes til å betegne likhet på matematisk språk er det av to parallelle og horisontale linjer, som i trykt tekst er det velkjente symbolet "=". Hvis du for eksempel har tre epler, kan du skrive følgende likhet:

Antall epler = 3

Uttrykket "antall epler" er medlem av venstre og nummer 3 er medlemmet til rettighetsretten.

Ettersom det er mulig å skrive numeriske beløp på forskjellige måter, brukes likhet for å betegne dem. Når du tar en spesifikk sak for å illustrere poenget, er det flere måter å skrive nummer 4 på, bortsett fra det mest åpenbare som er 4 = 4, kan følgende skrives, gjennom en matematisk likhet:

2 + 2 = 4
6 - 2 = 4
8 ÷ 2 = 4
2 × 2 = 4
2² = 4

Likheten som vises her er sann, men en likhet er kanskje ikke, for eksempel 10 + 5 = 20 er falsk, siden 10 + 5 = 15.

Sikkert leseren kjenner andre måter å skrive nummer 4. Merk at uttrykk på hver side av likhet kan være tall, ord, bokstaver som symboliserer mengder eller andre symboler, for eksempel:

x + 1 = 7
til²B - 1 = xy
f (x) = 2x²

Matematikere brukte ikke alltid likestillingssymbolet, så de gamle matematikkavtalene var veldig omfattende.

Det tilskrives matematikeren og doktor Robert Husk (1510-1558), født i Wales, opprettelsen av likestillingssymbolet "=", så kjent for alle i dag. Husk at tilsynelatende lei av å skrive til enhver tid uttrykket "akkurat som" i en av hans matematikkavtaler, bestemte han seg for å forkorte på sin plass de pårørende parallelle striper.

Kan tjene deg: femkantet prisme: egenskaper, deler, hjørner, kanter, volum

Egenskaper ved matematisk likhet

Følgende egenskaper tillater å fungere riktig med matematisk likhet. De er aksiomatiske, så de krever ikke demonstrasjon:

1.- Reflekterende eiendom

Denne egenskapen slår fast at ethvert beløp er lik seg selv. Siden et hvilket som helst tall er lik seg selv, kan det skrives like:

5 = 5

36.35 = 36.35

Hvis et beløp er bokstavelig, eller det er kombinasjon av bokstaver og tall, er den også lik seg selv:

3x = 3x

til²BC^-1 = a²BC^-1

2.- Eiendom av symmetri

Beløpene eller medlemmene på begge sider av likhet kan utveksles uten tapt gyldighet. Det vil si at hvis det som er til venstre for "=" -symbolet er skrevet til høyre for deg, og det som er til høyre er plassert til venstre, er det den samme likheten.

For eksempel tilsvarer uttrykk 5 + 2 = 7 denne: 7 = 5 + 2. På samme måten:

12 + 8 = 20; 20 = 12 + 8

x + 1 = 3; 3 = x + 1

x - z = y; y = x - z

3.- Transitiv eiendom

Denne egenskapen refererer til ekvivalensen av likhet. Hvis to likhet har et felles medlem, er de også de samme, siden generelt:

Hvis “x = y” og “y = z” så x = z

For å illustrere denne egenskapen, bør du vurdere disse to numeriske likhetene: 2 + 2 = 4 og 6 - 2 = 4. Siden begge er lik 4 (de har et felles medlem), kan følgende skrives, uten å miste noen gyldighet:

2 + 2 = 6 - 2

Et annet eksempel, denne gangen med bokstaver:

Ja x + 1 = 5

OG

A - B = 5

Så:

x+1 = a - b

4.- Avbestillingsegenskaper

En likhet endres ikke hvis det i begge medlemmene er det samme beløpet som legger til (eller trekker fra) og det blir besluttet å eliminere eller avbryte dette. Dette er summen av summen.

Ta som et eksempel følgende numeriske likhet der de 10 vises både i medlemmet av høyre og i den til venstre:

Det kan tjene deg: trigonometriske funksjoner: grunnleggende, i det kartesiske planet, eksempler, trening

2 + 2 + 10 = 6 - 2 + 10

Nummer 10 kan kanselleres uten at likestilling mister gyldigheten, og etterlater en annen kortere likhet og tilsvarer den forrige:

2 + 2 = 6 - 2

I likhet (10 ÷ 2) - 3 = 5 - 3 Heltallet - 3 tilhører begge medlemmer av likhet og fremstår som å legge til, kan derfor kanselleres og oppnå:

10 ÷ 2 = 5

Det skjer også med bokstavelige mengder, for eksempel:

Ja x + 2y + z = −a + b + z

Da kan "z" kanselleres, siden den finnes på begge sider av likhet som å legge til (og med samme tegn).

Ved å gjøre det resulterer det:

x + 2y = −a + b

Den kan også definere avbestillingsegenskapen for multiplikasjon. Hvis det samme beløpet C multipliserer begge medlemmer av likhet, kan dette beløpet kanselleres, for eksempel:

Cx = cy

Da kan C kanselleres for å oppnå ganske enkelt:

x = y

5.- Enhetlighetseiendom

En likhet forblir ufravikelig ved å legge til, trekke, multiplisere eller dele med samme mengde på begge sider av det samme.

For eksempel må det 8 + 5 = 13, hvis begge medlemmene multipliserer med et visst vilkårlig tall C = 2, gjenstår likestilling:

(8+5) × 2 = 13 × 2

13 × 2 = 26

Matematiske like klasser

Det er forskjellige typer matematisk likhet, så de er klassifisert for sin beste forståelse i:

-Identiteter, De er likhet der begge medlemmene er identiske:

2 = 2
x = x
2x = x + x

og så videre.

-Ligninger, Dette er likheter der en eller flere ukjente vises, og er sanne for visse verdier, det vil si at likhet ikke blir oppfylt for noen vilkårlig verdi, så de er også kjent som betingede likheter. Eksempler:

x + 1 = 5

x³ = 27

A + B = 40

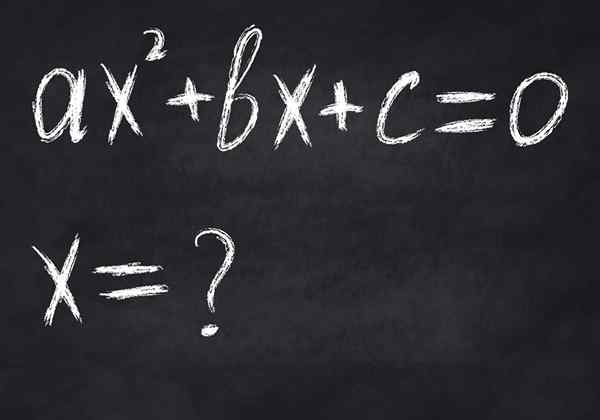Figur 2.- En ligning er en betinget matematisk likhet, siden den bare blir oppfylt for visse variable verdier. Bildet viser en andre grads ligning, som på det meste har to virkelige løsninger

-Ekvivalenser, I dem tilsvarer medlemmet til venstre for den til høyre, selv om de ikke er like, for eksempel i: 2³ = 8.

Kan tjene deg: Additive Principle

-Formler, Det er en likhet som alltid er oppfylt for verdiene til den uavhengige variabelen, som i den velkjente formelen for avstanden D avhengig av tidspunktet for en mobil med ensartet rettlinjet bevegelse: D = v ∙ t

Løste øvelser

Oppgave 1

Skriv nummer 10 til fire forskjellige og tilsvarende likhet.

Løsning

Alle disse likheten uttrykker nummer 10, men på forskjellige måter:

5 × 2 = 10

11-1 = 10

10¹= 10

20 ÷ 2 = 10

Oppgave 2

Hva er verdien av x som tilfredsstiller likhet x + 1 = 3?

Løsning

Denne likheten er en ligning, siden verdien av x er ukjent. Ved å bruke egenskap 5, hvis uttrykket x + 1 = 3 legges til (−1) på begge sider av symbolet "=", gjenstår likestilling:

x + 1 + (−1) = 3 + ( - 1)

Når du legger til (−1) til venstre medlem og operasjonen er løst, er "x" alene på venstre side av likhet, denne prosedyren kalles klarering:

x + 1 - 1 = 3−1

x = 2

Derfor er verdien som tilfredsstiller denne likheten x = 2.

Øvelse 3

Hvis en mobil med jevn rettlinjet bevegelse har en hastighet på 2.5 m/s, hva er avstanden som går etter 3 sekunder?

Løsning

Formelen sett i forrige seksjon brukes, D = v ∙ t, der verdien av V erstattes:

D = 2.5 ∙ t

Uttrykket blir en likhet når t = 3 sekunder og operasjonen løses:

D = 2.5 ∙ 3 m = 7.5m

Som resulterer i likhet:

D = 7.5m

Referanser

1. Barnett, r. 2000. Før-skulptur. 4. plass. Utgave. McGraw Hill.
2. Larson, r. 2012. Før-skulptur. 8. Utgave. Cengage Learning.
3. Pérez, v. Egenskaper for algebraisk likhet. Gjenopprettet fra: Matematikk.Laguia2000.com.
4. Egenskaper for likhet. Hentet fra: PPS.K12.Eller.oss.
5. Stewart, J. 2007. Forkalkning: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.