Gjensidig induktansformel/koeffisient, applikasjoner, øvelser

De gjensidig induktans beskriver samspillet mellom to kommende 1 og 2 spoler, hvor en variabel strøm Yo Sirkulerende gjennom spole 1, produserer en skiftende magnetfeltstrøm som krysser spole 2.

Denne flyten er proporsjonal med strømmen og proporsjonalitetskonstanten er gjensidig induktans₁₂. Være φ_B2 Magnetfeltet strømmer gjennom spole 2, så kan du skrive:

Φ_B2 = M₁₂ Yo₁

Figur 1.- Transformatoren er den viktigste anvendelsen av gjensidig induktans. Kilde: Pixnio.

Og hvis spole 2 har n₂ Runder:

N₂ . Φ_B2 = M₁₂ Yo₁

På denne måten gjensidig induktans eller gjensidig induktans koeffisient₁₂ Mellom begge spoler er:

M₁₂ = N₂ . Φ_B2 / Yo₁

Gjensidig induktans har Weber/Amperio eller WB/A -enheter, som kalles Henry eller Henrio og forkortet h. Derfor 1 Henry tilsvarer 1 wb/ a.

Verdien av m₁₂ Det avhenger av geometrien mellom spolene, deres form, deres størrelse, antall svinger på hver og avstanden som skiller dem, så vel som den relative posisjonen mellom dem.

[TOC]

Gjensidige induktansapplikasjoner

Fenomenet gjensidig induktans har mange anvendelser takket være det faktum at opprinnelsen er i Faraday-Lenz-loven, som sier at variable strømmer i en krets induserer strømmer og spenninger i en annen, uten behov for at kretsene skal kobles sammen med kabler av kabler.

Når to kretser samhandler på denne måten, sies det at de er magnetisk koblet. På denne måten kan energi gå fra hverandre, en omstendighet som kan brukes på flere måter, som demonstrert av Nikola Tesla på begynnelsen av 1900 -tallet (se øvelse løst 1).

I hans forsøk på å overføre strøm uten kabler, opplevde Tesla med forskjellige enheter. Takket være det.

Kan tjene deg: enhetsvektorer: egenskaper, hvordan få det ut, eksempler

Transformatoren

Transformatoren overfører svært høye alternative spenninger i de elektriske linjene, og minimerer dermed varmetap og leverer samtidig maksimal energi til forbrukerne.

Når spenningen når disse, må disse reduseres, noe som oppnås med transformatoren. Dette består av to trådspoler rullet rundt en jernkjerne. En av spolene med n₁ svinger er koblet til en alternativ spenning og kalles primær. Den andre, som er sekundær, har n₂ svinger, kobles til en motstand.

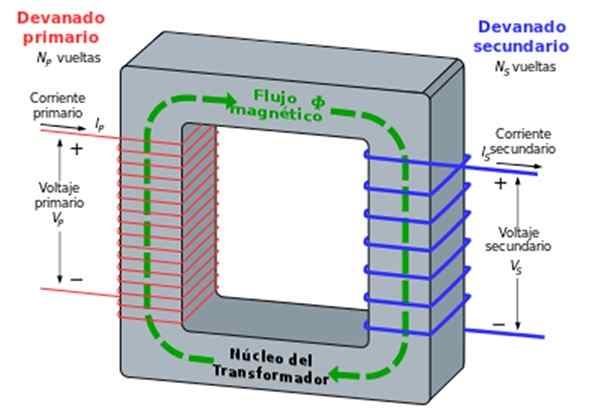Figur 2. Transformatoren. Kilde: Wikimedia Commons.

Jernkjernen sikrer at alle magnetfeltlinjer som passerer gjennom en spole også gjør det for den andre.

Faradays lov slår fast at årsaken mellom V -spenningene₂ /V₁ (sekundær /primær) er lik årsaken mellom antall svinger n₂ /N₁:

V₂ /V₁ = N₂ /N₁

Riktig justering av antall svinger, oppnås en spenning større eller mindre enn inngangen ved utgangen.

Transformatorene er bygget av mange størrelser, fra enorme transformatorer i elektriske installasjoner til mobiltelefonlastere, bærbare datamaskiner, mp3 og andre elektroniske enheter.

Pacemaker

Effektene av gjensidig induktans er også til stede i Pacemaker for å opprettholde hyppigheten av hjerteslag, slik at den kan holde blodstrømmen stabil.

Pacemakers jobber med batterier. Når de er utmattet, er en ekstern spole i stand til å overføre kraft til en annen spole inne i pacemakeren. Ettersom prosedyren utføres ved induksjon, er det ikke nødvendig å sende pasienten til et nytt inngrep når batteriet er utmattet.

Det kan tjene deg: Kalibreringskurve: Hva er det for, hvordan du gjør det, eksempler

Trådløse lastere

Mens en annen vanlig applikasjon er trådløse lastere for forskjellige objekter som tannbørster og mobiltelefoner, som er enheter med lite strømforbruk.

I fremtiden blir bruken av trådløse lastere for elbilbatterier hevet. Og mange forskning i dag er rettet mot å produsere trådløs elektrisitet i hjem. En av hovedbegrensningene for øyeblikkene er avstanden som strømningene kan induseres takket være magnetfeltene.

Løste øvelser

- Oppgave 1

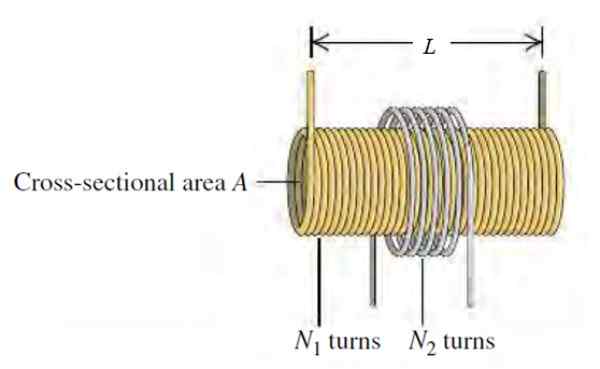
I en versjon av Tesla -spolen, brukt som en høyspenningsgenerator i noen laboratoriedemonstrasjoner, er det en lang lengde L, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R₁ med n₁ runde per enhetslengde, koaksialt omgitt av en sirkulær radiobin r₂ og n₂ runder.

Figur 3. Ordning av en Tesla -spole. Kilde: Sears Zemansky. Universitetsfysikk.

a) Finn den gjensidige induktansen m på kretsen, er det avhengig av strømmen som sirkulerer gjennom magnetventilen?

b) avhenger gjensidig induktans av spolenes form eller om svingene dine er mer eller mindre rullet sammen?

Løsning på

Størrelsen på magnetfeltet til magnetventilen er proporsjonal med antall svinger og strømmen som sirkulerer gjennom den, som er betegnet som jeg₁, Siden magnetventilen er krets 1. Det er gitt av uttrykket:

B₁ = μ_entenN₁.Yo₁ / L

Magnetfeltstrømmen som magnetventilen skaper i en spira av spolen, som er krets 2, er produktet av feltets intensitet av området koblet av feltet:

Φ_B2 = B₁. TIL₁

Hvor du skal₁ Det er området av tverrsnittet av magnetventilen og ikke av spolen, siden magnetfeltet er ugyldig utenfor det:

Det kan tjene deg: lysende kropper: egenskaper og hvordan de genererer sitt eget lys

TIL₁ = π (r₁)²

Vi erstatter området i ligningen for φ_B2:

Φ_B2 = B₁. π (r₁)² = (μ_entenN₁.Yo₁ / L). π (r₁)²

Og gjensidig induktans er gitt av:

M₁₂ = N₂ . Φ_B2 / Yo₁ = N₂. [(μ_entenN₁.Yo₁ / L). π (r₁)² ] / Yo₁

M₁₂ = μ_enten N₁ N₂ . π (r₁)² / L

Det avhenger ikke av strømmen som sirkulerer gjennom magnetventilen, som vi så at den er kansellert.

Løsning b

Som vi ser, avhenger ikke den gjensidige induktansen av spolenes form, og heller ikke når sokkene strammes. Den eneste påvirkningen av spolen i gjensidig induktans er antallet svinger i den, som er n₂.

- Oppgave 2

To spoler er veldig nær hverandre, og en av dem gjennomfører en variabel strøm i tiden gitt av følgende ligning:

I (t) = 5.00 e ^{-0.0250 t} Sen (377 t) a

På t = 0.800 sekunder Den induserte spenningen i den andre spolen måles, og oppnår -3.20 v. Finn den gjensidige induktansen til spolene.

Løsning

Vi bruker ligningen:

ε₂ = - m₁₂ (ga₁/dt)

Til gjensidig induktans blant spolene kaller vi det ganske enkelt, siden vanligvis m₁₂ = M_tjueen. Vi trenger det første derivatet av strømmen med hensyn til tid:

ga₁/dt =

= - 0.0250 x 5.00 e ^{-0.0250 t} x sin (377 t) - 377 cos (377 t) x 5.00 e ^{-0.0250 t}  Ess

Vi evaluerer dette derivatet i t = 0.800 s:

ga₁/dt = - 0.0250 x 5.00 e ^{-0.0250 x 0.800} x sin (377 x 0.800) - 377 cos (377 x 0.800) x 5.00 e ^{-0.0250 x 0.800}  A/s =

= -5.00 e ^{-0.0250 x 0.800} [0.0250 x Sen (377 x 0.800) + 377 cos (377 x 0.800)] =

= -1847.63 A/S

M = -3.20 V / -1847.63 A/S = 0.001732 H = 1.73 MH.

Referanser

1. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 6. Elektromagnetisme. Redigert av Douglas Figueroa (USB).
2. Hewitt, Paul. 2012. Konseptuell fysisk vitenskap. 5. plass. Ed. Pearson.
3. Knight, r.  2017. Fysikk for forskere og ingeniørfag: En strategitilnærming. Pearson.
4. Sears, f. (2009). University Physics Vol. 2.
5. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 2. 7. Ed. Cengage Learning.