Destruktiv interferensformel og ligninger, eksempler, trening

De destruktiv interferens, I fysikk oppstår det når to uavhengige bølger som kombineres i samme romområde er utdatert. Da møter ryggene på en av bølgene dalene til den andre, og resultatet er en bølge med en nullamplitude.

Flere bølger passerer uten problemer gjennom det samme punktet i verdensrommet, og deretter følger hver sin vei uten å bli berørt, for eksempel bølgene i vannet på følgende figur:

Figur 1. Regndråper produserer bølger på overflaten av vannet. Når de resulterende bølgene har null bredde, sies det at interferens er ødeleggende. Kilde: Pixabay.

Anta at to bølger med lik amplitude til og frekvens ω, som vi vil kalle og₁ og og₂, som kan beskrives matematisk gjennom ligninger:

og₁= En sen (kx -ω)

og₂ = En sen (kx -ωt + φ)

Den andre bølgen og₂ Det har et gap φ med hensyn til det første. Når de kombineres, siden bølger kan overlegges uten problemer, gir de opphav til en resulterende bølge som heter og_R:

og_R = y₁ + og₂ = En sen (kx -ω) + en sin (kx -ωt + φ)

Gjennom trigonometrisk identitet:

sin α + sin β = 2 sin (α + β)/2 . cos (α - β)/2

Ligningen for og_R Det forvandler seg inn:

og_R = [2a cos (φ/2)] Sin (kx - ωt + φ/2)

Nå har denne nye bølgen en resulterende amplitude til_R = 2a cos (φ/2), som avhenger av faseforskjellen. Når denne faseforskjellen skaffer seg verdiene+π eller -π, er den resulterende amplituden:

TIL_R = 2a cos (± π/2) = 0

Siden cos (± π/2) = 0. Nettopp da er det når ødeleggende forstyrrelser mellom bølger oppstår. Generelt sett, hvis argumentet til kosinuset er av formen ± kπ/2 med odd k, amplituden til_R  Det er 0.

[TOC]

Destruktive interferenseksempler

Som vi har sett, når to eller flere bølger passerer samtidig gjennom et punkt, overlapper de hverandre og gir opphav til en resulterende bølge hvis amplitude avhenger av faseforskjellen mellom deltakerne.

Kan tjene deg: lineær variasjon: konsept, eksempler, trening løst

Den resulterende bølgen har samme frekvens og bølgetall som de opprinnelige bølgene. I følgende animasjon er to bølger lagt over i blå og grønne farger. Den resulterende bølgen er i rødt.

Amplituden vokser når interferensen er konstruktiv, men den blir kansellert når den er ødeleggende.

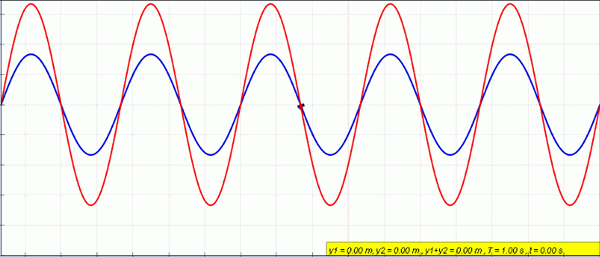Figur 2. Blå og grønnfargede bølger overlapper hverandre for å gi opphav til den røde bølgen. Kilde: Wikimedia Commons.

Bølgene som har samme amplitude og frekvens kalles Koherente bølger, så lenge de holder mellom dem den samme faseforskjellen φ. Et sammenhengende bølgeeksempel er laserlys.

Betingelse for destruktiv interferens

Når de blå og grønne bølgene er utdaterte i 180 º på et gitt punkt (se figur 2), betyr det at mens de beveger seg, har de Faseforskjeller φ av π radianer, 3π radianer, 5π radianer og så videre.

På denne måten, ved å dele argumentet om den resulterende amplituden med 2, resulterer det (π/2) radianer, (3π/2) radianer ... og kosinus av slike vinkler er alltid 0. Derfor er interferensen ødeleggende og amplituden gjøres 0.

Destruktiv bølgeforstyrrelse i vann

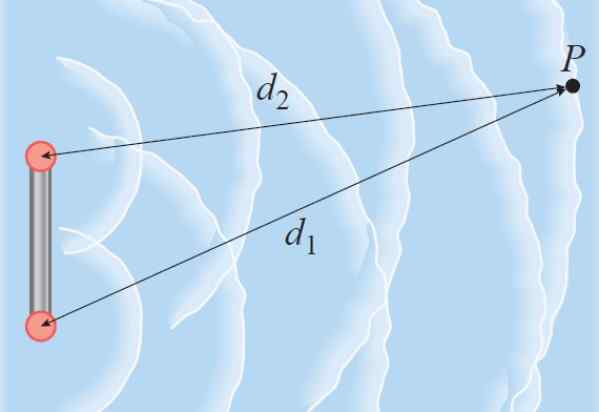
Anta at to sammenhengende bølger begynner i en med hverandre. Slike bølger kan være de som sprer seg gjennom vannet takket være to barer som vibrerer. Hvis de to bølgene reiser til samme punkt P, og turnerer på forskjellige avstander, er faseforskjellen proporsjonal med baneforskjellen.

Figur 3. Bølgene produsert av de to kildene reiser i vannet til punktet P. Kilde: Giambattista, a. Fysikk.

Som en bølgelengde λ tilsvarer en forskjell på 2π radianer, så er det sant at:

│d₁ - d₂│ / λ = Faseforskjell / 2π radianer

Faseforskjell = 2π x│d₁ - d₂│/ λ

Kan tjene deg: Polarisering av lys: Typer, eksempler, applikasjoner

Hvis veiene til veier er et oddetall bølge-semi-bølge, det vil si: λ/2, 3λ/2, 5λ/2 og så videre, er interferensen ødeleggende.

Men hvis veiforskjellen er et moment antall bølgelengder, er interferensen konstruktiv og amplituder tilsettes på punkt P.

Destruktiv forstyrrelse av lysende bølger

Lysbølger kan også forstyrre hverandre, som Thomas Young uttalt i 1801 gjennom deres berømte dobbeltspalteeksperiment.

Young ga lys gjennom en spalte laget på en ugjennomsiktig skjerm, som ifølge Huygens -prinsippet på sin side genererer to sekundære lyskilder. Disse kildene fortsatte på vei gjennom en annen ugjennomsiktig skjerm med to spalter og det resulterende lyset ble projisert på en vegg.

Diagrammet er observert i følgende bilde:

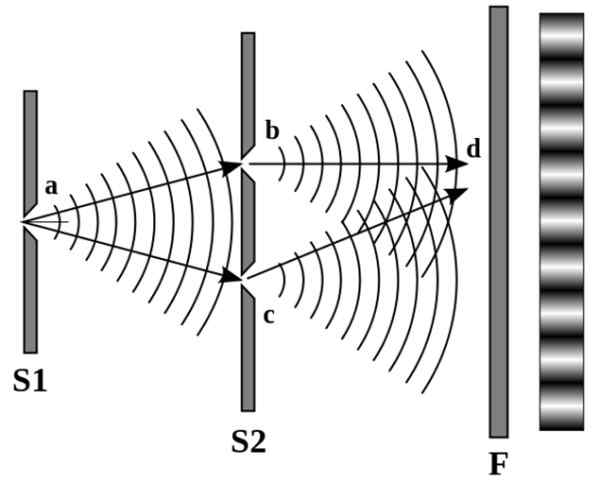Figur 4. Mønsteret med lys og mørke linjer på høyre vegg skyldes henholdsvis konstruktiv og destruktiv interferens. Kilde: Wikimedia Commons.

Young observerte et særegent mønster av alternative lys og mørke linjer. Når lyskilder forstyrrer destruktivt, er linjene mørke, men hvis de gjør konstruktivt, er linjene klare.

Et annet interessant interferenseksempel er såpebobler. Dette er veldig tynne filmer, der interferensen oppstår fordi lyset reflekteres og brytes på overflatene som begrenser såpefilmen, både over og under.

Figur 5. På en tynn såpefilm dannes et interferensmønster. Kilde: PXFuel.

Som filmens tykke. Resultatet er et fargemønster hvis hendelseslyset er hvitt.

Det er fordi det hvite lyset ikke er monokromatisk, men det inneholder alle bølgelengdene (frekvensene) til det synlige spekteret. Og hver bølgelengde ser ut som en annen farge.

Det kan tjene deg: lysende kropper: egenskaper og hvordan de genererer sitt eget lys

Trening løst

To identiske høyttalere som drives av samme oscillator er atskilt 3 meter og en lytter er 6 meter fra midtpunktet for separasjon mellom høyttalere, på punktet eller.

Gå deretter til punkt P, i en vinkelrett avstand på 0.350 av punktet eller, som vist på figuren. Der slutter å lytte til lyden for første gang. Hva er bølgelengden som oscillatoren avgir i?

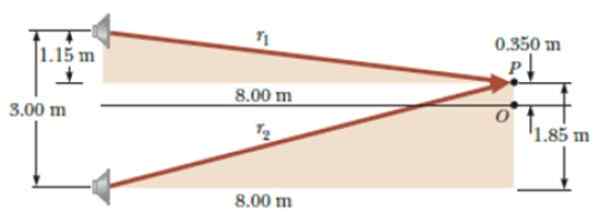Figur 6. Diagram for øvelsen løst. Kilde: Serway, R. Fysikk for vitenskap og ingeniørfag.

Løsning

Amplituden til den resulterende bølgen er 0, derfor er interferensen ødeleggende. Du må:

Faseforskjell = 2π x│r₁ - r₂│/ λ

Av Pythagoras teorem brukt på de skyggelagte trekantene på figuren:

r₁ = √1.femten² + 8² M = 8.08 m; r₂ = √1.85² + 8² M = 8.21 m

│r₁ - r₂│ = │8.08- 8.21 │ M = 0.13 m

Minimumene forekommer i λ/2, 3λ/2, 5λ/2 ... den første tilsvarer λ/2, da, av formelen for faseforskjellen er:

λ = 2π x│r₁ - r₂│/ faseforskjell

Men faseforskjellen mellom bølgene må være π, slik at amplituden til_R = 2a cos (φ/2) være null, da:

λ = 2π x│r₁ - r₂│/ π = 2 x 0.13 m = 0.26 m

Referanser

1. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 7. Bølger og kvantefysikk. Redigert av Douglas Figueroa (USB).
2. Fisicalab. Bølgeforstyrrelser. Gjenopprettet fra: Fisicalab.com.
3. Giambattista, a. 2010. Fysikk. 2. Ed. McGraw Hill.
4. Serway, r. Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.
5. Wikipedia. Søvnarkinterferens. Kilde: Det er.Wikipedia.org.