Lineær interpolering

Vi forklarer hva som er den lineære interpoasjonen, dens formler, hvordan du gjør en, med eksempler og øvelser løst

Hva er lineær interpolasjon?

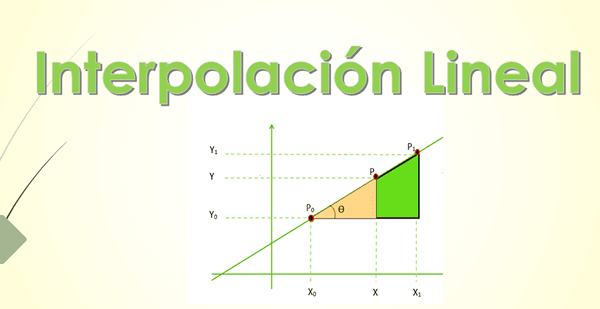
De Lineær interpolering Den består av å estimere plasseringen av et punkt innenfor et numerisk intervall, forutsatt at de ekstreme verdiene av nevnte intervall er forent av en linje. Kjent ligningen for denne linjen, er det mulig å finne det ukjente punktet.

Ideen er skjematisert i følgende figur, som viser en tilnærming til grafen til en funksjon mellom punkt A og B. Forutsatt at disse punktene er nært, er det mulig å tilnærme kurven som forener dem gjennom en linje og dermed finne mellompunktene.

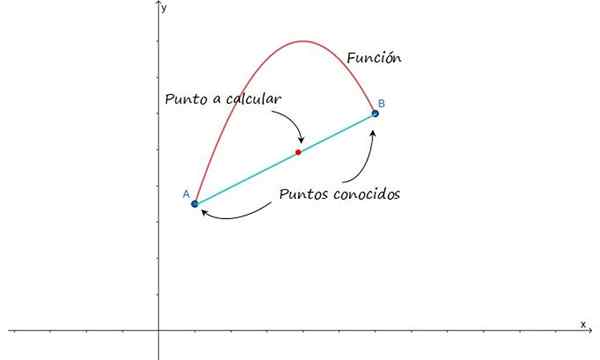Figur 1.- For å lage en lineær interpolasjon mellom punkt A og B, må det antas at de er forent med en linje . Kilde: f. Zapata.

Du kan også tilnærme kurven som blir med på punktene gitt ved hjelp av en kvadratisk funksjon eller annet polynom. Imidlertid har linjen fordelen med sin matematiske enkelhet, så det er lett å håndtere, selv om det er den enkleste interpolasjonen av alle, er det mulig at resultatet ikke er så presist som den som er oppnådd ved å bruke andre funksjoner.

Formler

Det er to koordinatpunkter [x_enten, f (x_enten)] og [x₁, f (x₁)] blant dem er poenget [x, g (x)], hvis koordinater er ønsket å vite.

Det første trinnet består i å slå sammen de kjente punktene gjennom et linjesegment, som koordinatene til punktet er en beregning er funnet.

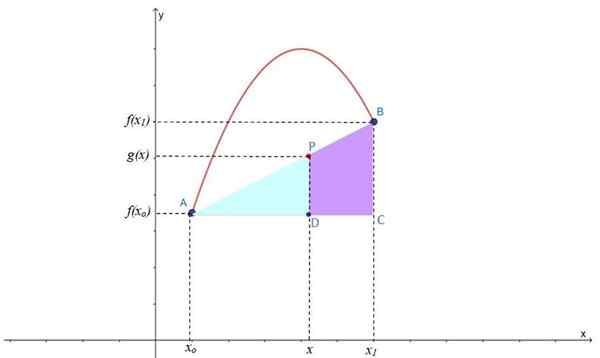Figur 2.- Lineær interpolasjon for å finne punkt P på den interpoching -linjen G (x), plassert mellom punkt A og B av F (x). Kilde: f. Zapata.

Som du kan se, dannes to rektangler: ABC og APD, som også har en akutt vinkel til felles, så de er lignende trekanter, som Thales -teoremet kan brukes til:

Det kan tjene deg: analytisk geometri

Ved å erstatte målet på segmentene i henhold til grafen oppnås følgende forhold:

Derfra fortsetter vi til å fjerne G (x):

 Ringer:

F₁(x₁) = y₁ ; F_enten(x_enten) = y_enten ; g (x) = y

Toppligningen blir omgjort til:

Feilområde

Når en funksjon nærmer seg med denne metoden, blir feilnivået gitt av den absolutte verdien av forskjellen mellom funksjonen f (x) og interpolasjonslinjen G (x):

Feil = │f (x) - g (x) │

Hvordan lage lineær interpolasjon?

Å utføre en lineær interpolasjon er veldig enkel, du må bare følge disse trinnene:

Trinn 1

Bestem det ukjente punktet P (x, y).

Steg 2

Etablere de to punktene som begrenser intervallet der verdien som skal beregnes er lokalisert, det vil si punktene (x x_enten,og_enten) og (x₁, og₁).

Trinn 3

Erstatte alle verdier i ligningen:

Og beregne resultatet.

Eksempler på lineær interpolasjon

Eksempel 1

Du vil finne den omtrentlige verdien av Ln 3 gjennom lineær interpolasjon, gitt følgende verdier:

Ln 2 = 0.693147 og ln 4 = 1.386294

Sammenlign resultatet med verdien av Ln 3 oppnådd gjennom en kalkulator og bestemme marginen som er forpliktet.

• Trinn 1

For å finne den omtrentlige verdien av ln 3 må du fortsette etter måte: For det første er det ukjente etablert, som er y = ln 3, ved siden av den tilsvarende verdien av "x": x = 3. Dette er poenget du vil beregne: (3, LN 3).

• Steg 2

Da må du etablere grensepunktene for intervallet med de kjente verdiene. Det blir bedt om å gjøre det med de neste par poengene:

• Nedre grense: [x_enten = 2; og_enten = ln 2 = 0.693147]
• Øvre grense: [x₁ = 4; og₁ = ln 4 = 1.386294]

• Trinn 3

Verdiene som er bestemt i trinn 1 og 2 erstattes nøye i ligningen for å generere resultatet av tilnærmingen til Ln 3:

Kan tjene deg: hvor mange løsninger har en kvadratisk ligning?

Den virkelige verdien av Ln 3 oppnådd av kalkulatoren er:

ln 3 = 1.098612

Og feilmarginen er:

Feil = │1.098612 - 1.03971 │ = 0.059

Den prosentvise feilen for interpolasjonen beregnes ved å dele feilen mellom den reelle verdien av LN3 og multiplisere med 100 %:

Prosentvis feil = (ekte feil/verdi) × 100 = (0.059/1.098612) × 100% = 5.4%

Eksempel 2

Nå vil du finne den omtrentlige verdien av Ln 3 ved lineær interpolasjon, kjent disse to verdiene:

ln 2.5 = 0.916291 og ln 3.5 = 1.252763

Bestem også den tilsvarende feilen og sammenlign med resultatene fra forrige eksempel.

• Trinn 1

Igjen er det ukjente poenget:

y = ln 3, x = 3

• Steg 2

• Nedre grense: [x_enten = 2.5; og_enten = y_enten = ln 2.5 = 0.916291]
• Øvre grense: [x₁ = 3.5; og₁ = ln 3.5 = 1.252763]

• Trinn 3

Undersøkelse av verdien som kalkulatoren tilbyr:

ln 3 = 1.098612

Feilnivået bestemmes i dette tilfellet, noe som resulterer:

Feil = │1.098612 - 1.084527 │ = 0.014

Prosentvis feil i dette tilfellet er ≈ 1.3 %. Sammenlignet med feilnivået i eksempel 1, er den nye verdien mer presis, siden intervallet som er valgt til interpolar er lavere.

Løste øvelser

Oppgave 1

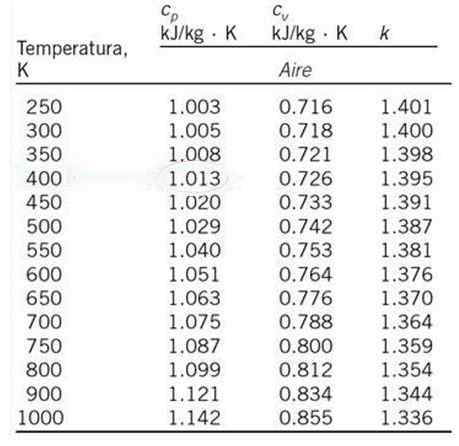
Beregn ved lineær interpolasjon, den spesifikke varmen av luften ved konstant trykk C_p  og temperatur på 530 K, med start fra tabellen med verdier vist nedenfor.

• Løsning

I oppløsningen av mange problemer er det vanlig at verdien som blir søkt ikke vises nøyaktig som ønsket i tabellen med verdier for hånden. Et alternativ er å velge verdien nærmest ønsket, men mange ganger er en lineær interpolasjon nok til å finne en mye bedre tilnærming.

Kan tjene deg: tegn på gruppering

Verdien av C_p En 530 K vises ikke i det vedlagte tabellen, men en lineær interpolasjon kan gjøres med de respektive spesifikke varmen ved 500 K og 550 K, som er temperaturene nærmest 530 K og hvis spesifikke varmer vises i tabellen vist.

Den respektive spesifikke varmevarmen for disse temperaturene er:

T_enten = 500 K; c_Po = 1.029 kJ /kg ∙ k

T₁ = 550 K; c_P1 = 1.040 kJ /kg ∙ k

Og det ukjente er poenget (500K, C_p)

Erstatte i formelen til den lineære interpolasjonen gitt ovenfor, med t på scenen til variabelen "x" og c_p I stedet for "y", har du:

Oppgave 2

Belastningen påført en fjær (i Kilopondios) produserer følgende forlengelser (i millimeter) i henhold til tabellen som er vist:

Beregn forlengelse når belastningen er 12.6 kp.

• Løsning

La og verdien av forlengelsen søkt når belastningen er C = 12.6 kp. Det ukjente punktet er (12.6, y), som er blant poengene:

C_enten = 10 kp; og_enten = 105 mm

C₁ = 15 kp; og₁ = 172 mm

Det gjenstår bare å erstatte verdiene i ligningen:

Foreslått trening

Beregn den spesifikke varmevarmen til et konstant volum for en temperatur på 727 K, ved bruk av lineær interpolasjon og tabellen over verdipapirer av øvelsen løst 1.

Referanser

1. Rafa Vilchez Academy. Hvordan utføre lineær interpolasjon. Gjenopprettet fra: Academiraafavilchez.com
2. Chapra, s. 2007. Numeriske metoder for ingeniører. 5. plass. Utgave. McGraw Hill.
3. Khan Academy. Matematikk av lineær interpolasjon. Gjenopprettet fra: Khanacademy.org.
4. Utdanningslivet. Lineær interpolasjonsformel. Gjenopprettet fra: TheEducationLife.com
5. X-Engineer. Lineær interpolasjon og ekstrapolering med kalkulator. Gjenopprettet fra: X-Engineer.org.