Homologe sider

Vi forklarer hva de homologe sidene er, med eksempler og øvelser løst

Hva er homologe sider?

De homologe sider I to flate geometriske figurer er de som tilsvarer hverandre, og holder likhet. For eksempel er en persons høyre hånd homolog med en annen persons høyre hånd.

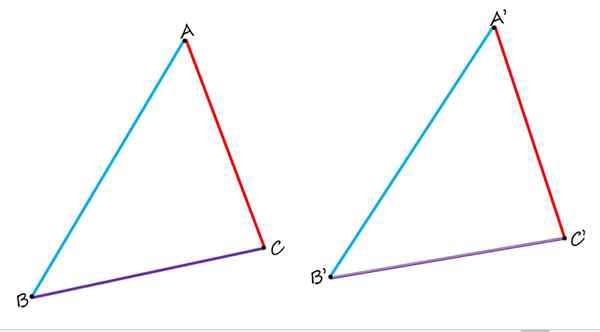
I flat geometri er det ikke bare homologe sider, men hjørner og homologe vinkler også. For å se det, bør du vurdere følgende figur, som består av to identiske trekanter ABC og A'B'C ':

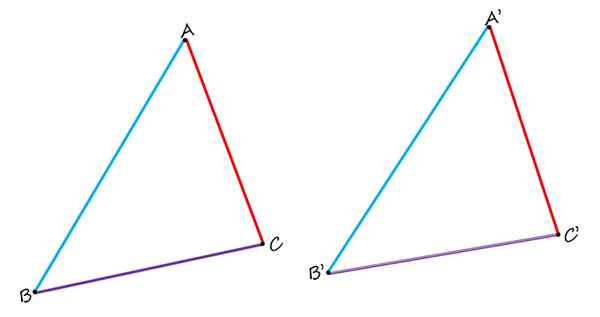I de to identiske trekantene som er vist, er AB og A'B ', homologe, så vel som Sides BC og B'C' og AC og A'C '. Kilde: f. Zapata.

Når man sammenligner dem, observeres det tydelig at sidene AB og A'B 'i blått er homologe, ettersom de inntar en lignende posisjon i hver trekant. Sidene bc og b'c 'i lilla er også homologe. Og til slutt er den røde AC -siden homolog med siden A'c '.

Forklaring

Fra de nevnte følger det at de homologe sidene er de som inntar den samme relative posisjonen i figurer på samme måte. I det forrige bildet ble to identiske trekanter brukt for å vise ideen, men dette kan lett generalisere andre flate geometriske figurer, dannet av påfølgende sider som lukker.

Disse tallene kalles Polygoner. For eksempel er trekanter og firkantede polygoner på henholdsvis 3 og 4 sider.

Begrepet homologe sider er viktig fordi det tillater å definere kriterier for likhet mellom polygoner, som det vil bli sett snart. De lignende figurene har nøyaktig samme form og holder identisk andel mellom sidene, selv om de ikke er i samme størrelse.

Og selv om det hittil bare ble henvist til flate figurer, er det også lignende figurer i tre dimensjoner. De blir lett observert i supermarkedshyllene, når det samme produktet selges i identiske containere, men med en annen størrelse.

Kan tjene deg: matematisk logikk

Andre ord som brukes om hverandre i geometri for å referere til homologe sider i geometriske figurer er: tilsvarende sider, respektive sider og tilsvarende sider.

Homologe hjørner og vinkler

Som med sidene er også homologe hjørner definert, som forener par homologe sider. For eksempel er hjørner a og 'fra forrige figur homologe. Tilsvarende er parene med hjørner B og B 'og C og C' homologe.

Til slutt inntar homologe vinkler den samme relative posisjonen i figurene. Vertivene til homologe vinkler er igjen homologe.

For å illustrere ideen, ta vinkelen mellom de blå og lilla sidene av venstre trekant, som kan betegnes som ∠ABC. Denne vinkelen har sin motpart i vinkelen ∠A'B'c ', fra trekanten til høyre.

Vissenten til denne vinkelen er B, som som tidligere indikert er et motstykke med B ', og de to andre parene av homologe vinkler på trekantene som er vist er:

• ∠BCA og ∠B'C'a '
• ∠CAB og ∠C'A'B '

Likheten mellom polygoner

For at to polygoner skal være like, må følgende forhold være oppfylt:

• Alle par homologe vinkler har samme mål
• Hans par homologe sider er proporsjonale.

De to forholdene må oppfylles samtidig for å sikre likhet. Det blir umiddelbart observert hvorfor.

I den følgende figuren er det to firkantede som åpenbart ikke er like. Det skyldes at den første statusen til ukentlig er oppfylt, men den andre gjør det ikke:

To firkantede som ikke er like, selv om deres homologe vinkler har like store mål. Kilde: f. Zapata.

Mens i figurene deres par av homologe vinkler har samme mål, fordi alle er rette vinkler (de måler 90º), er figurene ikke like, fordi siderparene deres ikke er proporsjonale.

Kan tjene deg: Injeksjonsfunksjon: Hva den består av, hva er det for og eksempler

På den annen side har disse to firkantede sider homologe sider med like mål, men de homologe vinklene måler ikke det samme. Derfor er tall tydeligvis ikke like.

To firkantede med homologe sider av samme mål, men med forskjellige indre vinkler er de derfor ikke lignende figurer. Kilde: f. Zapata.

Likhetsgrunner

Hvis to figurer er like, er kvotienten mellom de homologe sidene den samme og kalles Likhetsgrunner.

Betegner sidene av en av figurene som a, b, c, d ... og de tilsvarende av den andre figuren som en ', b', c ', d

Omkrets og områder med lignende figurer

Likhetsforholdet gjør det mulig å oppnå sammenhenger mellom omkrets, områder og volum av to lignende figurer.

Omkretsårsaken til to lignende figurer

Omkretsen til en polygon er definert som summen av alle sidene. Hvis du har en figur hvis sider er en ', b', c ', d' ..., er dens omkrets p ':

P '= a' + b ' + c' + d '.. .

Hvis en annen polygon ligner på dette, og sidene er A, B, C, D ..., blir det oppfylt at:

Og derfor:

A = r ∙ a '

Du kan bekrefte det samme for de andre sidene av denne figuren. Så omkretsen P uttrykkes som:

P = A + B + C + D .. . = r ∙ a ' + r ∙ b' + r ∙ c ' + r ∙ d' + ..

Siden "R" er en vanlig faktor for alle rusavhengige, er forholdet mellom P og P ':

P = r ∙ p '

Dette betyr at årsaken til omkretsene mellom to lignende polygoner er lik årsaken til likhet.

Årsak til områder med to lignende figurer

Hvis henholdsvis to lignende figurer har områder A og A ', er disse relatert til:

Kan tjene deg: formelklaringøvelser

A = r²∙ a '

Hvor "r" er årsaken til likheten i figurene.

Volumforholdet på to lignende figurer

De er to lignende tre -dimensjonale figurer, hvis volum er henholdsvis V og V '. Forholdet mellom dem, gjennom "R" er:

V = r³∙ V '

Eksempler

Blåkopier

Deler av et land, anlegget av en bygning eller til og med et plagg, i mindre skala på et papirark kan bli representert. Planene har fordelen av å kunne ta med seg og gjøre de relevante modifikasjonene enkelt, før de blir utført på det virkelige objektet.

Kart

De er vanligvis representasjoner i flyet til et stort landområde, fra en landsby til kontinenter. De er også laget i en viss skala.

De har mange applikasjoner, og det er mange typer. Gjennom et kart kan for eksempel terrenget beskrives, og når det ligger på et bestemt punkt, blir den beste ruten å gå fra det tidspunktet til et annet bestemt.

Modeller

De er tre -dimensjonale representasjoner i omfanget av gjenstander som biler, bygninger og konstruksjoner generelt.

Trening løst

Følgende verdier tilsvarer sidene av et par lignende trekanter. Finn årsaken til likhet og verdier av "x" og "y":

Trekant 1: 5, 8, 10

Triangle 2: 150, x, y

Løsning

Årsaken til likhet er kvotienten:

R = 150/5 = 30

Derfor:

x = 30 × 8 = 240

y = 10 × 30 = 300