Ficks lov

Hva er Ficks lov?

De Ficks lov Det er en matematisk ligning som relaterer massestrømmen formidlet i et medium med konsentrasjonen eller trykkgradienten. Det ble formulert i 1855 av tysk fysiolog og doktor Adolf Fick, som inspirert av Fouriers lover (termisk ledning) og OHM (elektrisk ledning), modellerte prosessen med diffusjon av oksygen til alveolene i lungene.

Ficks lov presenterer det spesifikke at den ikke bare er gjeldende for kjemiske eller biokjemiske diffusjonsfenomener, men for de av noen form for natur. Derfor tjener det til å modellere formidling av atomer mellom faste stoffer, og er veldig nyttig i fysikken i materialer og ingeniørfag.

Representasjon av en diffusjonsprosess gjennom en semipermeabel membran. Kilde: Gabriel Bolívar.

Imidlertid er den sentrale basen den samme for nesten alle diffusjonsfenomener, som er illustrert ovenfor. Lilla partikler, være atomer eller molekyler, spres gjennom et semipermeabelt tykk membran L og tverrgående område til. Til venstre har vi en større konsentrasjon C₁ av partikler som til høyre, c₂.

Ficks lov etablerer følgende: massestrømmen som formidles gjennom en overflate er proporsjonal med konsentrasjonsgradienten (C₂-C₁/L) og en konstant d kalt diffusjons- eller diffusivitetskoeffisient.

Denne loven har to former: en basert på rom (x), og en annen avhengig av rom og tid (x, t). Den første gjelder systemer under stasjonære forhold, mens den andre for reelle, ikke -stasjonære systemer.

Ficks første lov

Komponenter og ligning

Den tykke l av den semipermeable membranen representerer avstanden (x) som partiklene må reise for å nå den andre siden. Som det fremgår av bildet, flytter lilla partikler jo mer de beveger seg bort fra venstre rom, der C₁ Det er flott, konsentrasjonen avtar til verdien av C₂. Det vil si at konsentrasjonen endres langs membranens tykkelse, og er avhengig av x.

Denne konsentrasjonsvariasjonen avhengig av avstand er det som kalles konsentrasjonsgradient: (C₂-C₁)/L O (C₂-C₁)/x. Merk at verdien er negativ (-1), fordi C₂ > C₁.

På den annen side har vi også den hastigheten som partiklene er spredt gjennom membranen eller det aktuelle rommet. Denne hastigheten avhenger av størrelsen og massen til partiklene, så vel som miljøets og temperaturens natur. Diffusjonskoeffisienten D representerer denne hastigheten, og kan være konstant eller ikke under diffusjon.

Kan tjene deg: laboratoriefilter): Kjennetegn, funksjoner, typer

Og til slutt har vi en massestrøm 'J' som krysser det tverrgående området til membranen eller kanalen der partiklene sprer seg. Grupperer disse begrepene, er ligningen for Ficks første lov født:

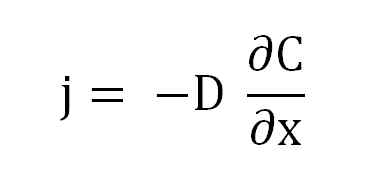Ligning av Ficks første lov. Kilde: Gabriel Bolívar.

Hvor J er proporsjonal med D og A (∂c/∂x), konsentrasjonsgradienten.

Tolkning og enheter

Det negative symbolet i ligningen tjener til å nøytralisere det negative tegnet på konsentrasjonsgradienten. Ellers ville J ha en negativ verdi, som er ubehagelig. På samme måte er verdien av D positiv, slik at det ved å multiplisere med det negative tegnet som går foran det, gir en negativ verdi.

Ficks første lov indikerer følgende: jo større konsentrasjonsgradient (∂c/∂x), jo større er massestrømmen j. Det vil si forskjellen mellom C₂ og c₁ Det blir større, og derfor vil flere partikler spre seg gjennom membranen.

På den annen side avhenger J også av D, som igjen er avhengig av parametere som temperatur, viskositet, molekylvekt og det tverrgående området til:

D ∝ (A/L) (S/√M_W)

Hvor s er løseligheten til partikkelen som er spredt med miljøet, og m_W Dens molekylvekt.

Angående enhetene til komponentene eller vilkårene for ligningen vi har:

-C (kg · m^-3 eller mol · m^-3)

-D (m^-2· S^-1)

-J (kg · m^-2· S^-1 eller mol · m^-2· S^-1)

Netto middels kvadratisk forskyvning

Under formidlingen kolliderer partiklene med hverandre, og etter korte tidsintervaller ender opp med å reise store avstander Δx. Avhengig av betydningen av disse forskyvningene kan Δx imidlertid ha negative eller positive verdier (i henhold til et opprinnelsespunkt). Det er grunnen til at gjennomsnittet av Δx -verdiene for alle molekyler har en tendens til 0.

På den annen side er Δx -verdiene veldig små sammenlignet med avstandene som kjører partiklene. Når de kolliderer, mister de mobilitet mot en retning, og har følgelig en begrenset netto forskyvning; For eksempel går 2 cm i en retning etter å ha reist hundrevis av meter i kollisjoner og returer.

Einstein i 1905 fant et matematisk uttrykk for den gjennomsnittlige rulle av forskyvningen (derfor forskjellig fra 0):

<(Δx)²> = 2DT

Definere

(Δx)_RMS ≡ <(Δx)²>^1/2 = (2DT)^1/2

(Δx)_RMS Det er den gjennomsnittlige netto kvadratiske forskyvningen av de aktuelle partiklene. (Δx)_RMS Den forteller oss hvor mye partikler beveger seg i gjennomsnitt (i en positiv eller negativ retning) i henhold til tiden. Noen partikler vil bevege seg videre eller nærmeste avstander enn (Δx)_RMS, forårsaker en gaussisk distribusjon.

Kan tjene deg: kalsiumoksid (CAO)

Fick Second Law

Ligning

Ficks første lov beskriver diffusjonen under stasjonære forhold, det vil si massestrømmen J varierer ikke over tid. I reelle systemer har vi imidlertid ikke -stasjonære forhold, der massestrømmen ikke bare varierer i verdensrommet, men også over tid. Derfor er det interessert i å bestemme (∂c/∂t).

Nedenfor har vi to ligninger som representerer Ficks andre lov:

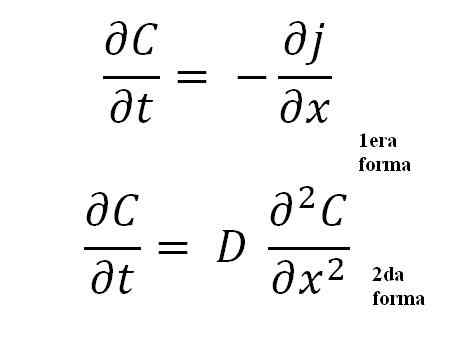Ligninger av Ficks andre lov. Kilde: Gabriel Bolívar.

Den andre formen er den viktigste av alle, ettersom den representerer den generelle matematiske ligningen for enhver formidlingsprosess; enten termisk, elektrisk, atomisk osv.

Fradrag

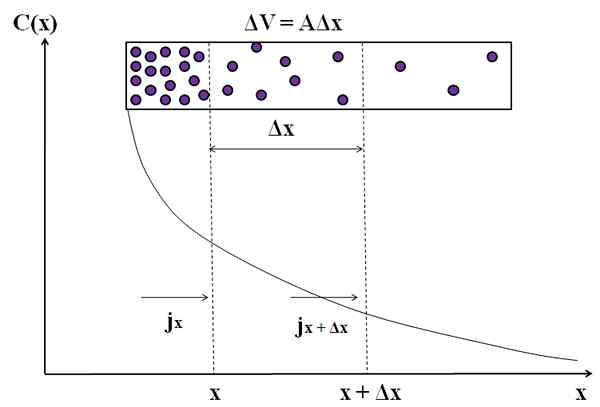Grafisk representasjon av hvordan massestrømmen ikke er konstant i formidlingen av disse molekylene. Kilde: Gabriel Bolívar.

Vurder igjen lilla partikler i et rektangulært kammer. Blant avstandene x og x+Δx har vi en flyt j_x (innkommende) og j_x+Δx (utgående). Kameraets volum mellom disse avstandene er definert av:

ΔV = Aδx

Merk at graf C (x) vs x ikke stammer fra en rett linje, så vi har forskjellige verdier av j (J_x ≠ J_x+Δx). Vi må bestemme ΔC/ΔT.

Massen m_x Det vil være lik:

m_x = J_x AΔt

En dimensjonal analyse hjelper til med å forstå hvorfor:

kg = (kg · m^-2· S^-1) (m²) (S)

På samme måte som vi beregner m_x+Δx:

m_{x+ Δx} = J_x+Δx AΔt

Å være massen som samler seg i den regionen lik ΔM:

Δm = m_x - m_{x+ Δx}

= (J_x - J_{x+ Δx}) AΔt

= -(J_{x+ Δx} - J_x) AΔt

= -ΔjaΔt

Og å vite at ΔC = ΔM/ΔV

ΔC = -ΔjaΔt/ ΔV

= -ΔjaΔt /aΔx

= -ΔjΔt/Δx

Vi fjerner ΔC/Δt

ΔC/Δt = -Δj/Δx

Dette uttrykket indikerer at variasjonen av konsentrasjonen over tid er lik variasjonen av J -strømmen med hensyn til dens forskyvning. Ved å bruke grensene for ΔT og Δx som har en tendens til 0 får vi det samme uttrykket som et delvis derivat:

∂c/∂t = -(∂j/∂x) (1. form)

Til slutt oppnås den andre formen ved å erstatte J med Ficks første lov:

∂c/∂t = -∂/∂x (-d∂c/∂x)

= D (∂²C/∂x²) (2. form)

Løste øvelser

I de følgende øvelsene vil veldig enkle systemer bli vurdert hvis ukjente kan løses ved hjelp av Ficks første lov.

Oppgave 1

Uttalelse

I et rør 15 meter langt og 21 centimeter bredt, og som også er mettet med nitrogen, er en oksygenstrøm spredt fra den ene enden til en annen ved en temperatur på 0 ºC. Å vite at trykket på venstre side (s₁) er 20 kg/m³, Og at trykket på høyre side (s₂) er 10 kg, bestem:

Det kan tjene deg: Hydronio ion

a) Massestrømmen som er spredt

b) hvor mange kilo av eller₂ De vil spre seg gjennom røret om 17 minutter?

c) Konsentrasjonsgradienten eller trykk

d) trykket på o₂ i en avstand på 7 meter fra inngangen til rørledningen

e) Hvor mye vil 80 kg o o₂ i spredning gjennom dette røret?

Tenk på at d_O2-N2 er lik 1.8 · 10^-5 m²· S^-1.

Vedtak

Fra Ficks første lov må vi løse underavsnitt A):

J = -D (P₂-P₁)/L

= -(1.8 · 10^-5 m²· S^-1) (10-20) (kg/m³)/(15 m)

= 1.2 · 10^-5 kg · m^-2· S^-1

Til B) Vi trenger rørområdet:

A = π (0.21 m)²

= 0.14 m²

Og vi multipliserer j med en og tid t for å bestemme massen av eller₂ Avskaffet:

m_O2 = (1.2 · 10^-5 kg · m^-2· S^-1) (17 s) (0.14 m²)

= 3.57 · 10^-5 kg

Nå, for underavsnitt C) har vi at gradienten er lik:

Gradient = (P₂-P₁)/L

= (10-20) (kg/m³)/15 m

= -2/3 (kg/m³) · M^-1

Men vi tar den positive verdien, noe som gir fysisk mening:

2/3 (kg/m³) · M^-1

Denne verdien vil da tjene oss til å løse underavsnittet d) hvis gradienten tolkes godt: hver meter trykket på eller₂ 2/3 kg/m vil falle³. Ved å spre 7 meter vil vi ha:

2/3 (kg/m³) · M^-1 (7 m) = 14/3 eller 4.7 kg/m³

Det vil si at trykket i den avstanden vil være:

(20-4.7) (kg/m³) = 15.3 kg/m³

Og til slutt er avsnitt E) lik B), bare at vi nå klarer tid og ikke massen:

m_O2 = Jat

t = m_O2/Ja

= (80 kg)/(1.2 · 10^-5 kg · m^-2· S^-1) (0.14 m²)

= 47619.04 s eller 0.55 dag

Oppgave 2

Uttalelse

Bestem (Δx)_RMS For sukrose i vann ved t = 1 min, 1 time og 1 dag. Formidlingskoeffisienten for sukrose i vann er 0.52 · 10^-5CM²· S^-1.

Vedtak

Vi bruker ligningen:

(Δx)_RMS ≡ <(Δx)²>^1/2 = (2DT)^1/2

Vi evaluerer (Δx)_RMS Med tidene uttrykt i sekunder. For t = 1 min eller 60 s:

(Δx)_RMS = ((2 (0.52 · 10^-5CM²· S^-1) (60 -tallet))^1/2

= 0.025 cm

For t = 1 time eller 3600 s:

(Δx)_RMS = ((2 (0.52 · 10^-5CM²· S^-1) (3600 -tallet)))^1/2

= 0.19 cm

Og til slutt for t = 1 dag eller 86400 s:

(Δx)_RMS = ((2 (0.52 · 10^-5CM²· S^-1) (86400s)))^1/2

= 0.95 cm

Merk at når tiden går av sukrose -molekylene, ikke engang har klart å bevege seg 1 cm i noen retninger.

Referanser

1. Walter J. Moore. (1963). Fysisk kjemi. I kjemisk kinetikk. Fjerde utgave, Longmans.
2. Iran. Levine. (2009). Prinsipper for fysikjemi. Sjette utgave. Mc Graw Hill.
3. Introduksjon til materialvitenskap og ingeniørfag. (11. mars 2018). Ficks andre lov. Prof. Rajesh Prasad. [Video]. Gjenopprettet fra: YouTube.com
4. Wikipedia. (2020). Ficks diffusjonslover. Hentet fra: i.Wikipedia.org
5. Laura Dickson. (10. september 2020). DIFFUSJON. Kjemi librettexts. Gjenopprettet fra: Chem.Librettexts.org
6. Larissa Zhou et al. (1. september 2015). Forstå diffusjonsteori og Ficks lov gjennom mat og matlaging. Det amerikanske fysiologiske samfunn. gjør jeg.org/10.1152/Advan.00133.2014