Kjemi

Lov om flere proporsjoner

Lov om flere proporsjoner

Hva er loven om flere proporsjoner?

De Lov om flere proporsjoner Det slår fast at hvis to elementer dannes mer enn en forbindelse når de reagerer på hverandre, så er andelen av massene som en av dem kombineres med en fast masse av den andre, det er lik et forhold av små tall.

Lovens uttalelse kan virke sammensatt hvis du ikke har et eksempel for hånden. Vurder derfor noen Oreos -informasjonskapsler, sammensatt av to sjokoladelokk og en stripe med sukkerholdig krem: T2C (t = lokk og c = krem). Hvis vi ønsket å finne opp en mer robust Oreo -informasjonskapsel, ville vi lagt til en annen stripe med krem, for å ha dobbeltkrem (t2C2 eller TC).

I desserter, for eksempel Oreos -informasjonskapsler, har vi proporsjoner som kan varieres bare for å forberede andre versjoner av dem. Kilde: Brokensphere, CC BY-SA 3.0 https: // creativecommons.Org/lisenser/by-SA/3.0 via Wikimedia Commons

Vi kan også legge til en annen, slik at cookien har tre ganger mer krem ​​enn en konvensjonell cookie (t2C3). Hva om vi legger et annet sjokoladelokk midt i de hvite stripene (t3C2)? Alternativene er ubegrensede; Men vi legger alltid til et lokk eller kremenhet. Vi tenker ikke på halvparten av lokket (1/2 t), eller en femtedel av krem ​​(1/5 c), fordi det ville være upassende.

På samme måte skjer det med de kjemiske elementene: Atomene deres deler ikke for å danne forbindelser. Derfor "massene av T eller C blant forbindelsene" alltid "et enkelt forhold.

Forklaring

Proporsjoner

Loven om flere proporsjoner, sammen med loven om de definerte proporsjonene, gikk foran støkiometrien og de første kjemiske formlene. La oss glemme informasjonskapslene, men la oss beholde symbolene sine: T og C. Gjennom eksperimenter oppdages det at elementer T og C danner flere forbindelser: T2C, TC og T2C3.

Før de kjemiske formlene var det umulig å vite med en gang som var proporsjonene av massene av T og C i slike forbindelser. Måtte først bestemme dem. I en forbindelse ble det oppdaget at massen av T doblet seg til C; Å si, 2 gram t er kombinert med 1 gram c.

Kan tjene deg: kapasitans: enheter, formler, beregning, eksempler

Da, i de andre forbindelsene, måtte massene av T og C matches: 2 gram t er nå kombinert med 2 gram C C. Her oppstår spørsmålet: Hva om T og C fortsatt kan danne en annen forbindelse? I så fall vil det sikkert bli dannet med 2 gram t, men denne gangen ville de bli kombinert med 3 gram C (1 gram + 1 gram + 1 gram).

Enkle masseforhold

Andelene av massene som T og C reagerer tillater å etablere sine kjemiske formler: T2C (2 gram t: 1 gram c), tc (2 gram t: 2 gram c) og t2C3 (2 gram t: 3 gram c). Hvis vi ønsker å sammenligne forholdene til T- eller C -massene i disse forbindelsene, er det nødvendig at en av massene forblir konstant; I dette tilfellet av t: 2 gram.

Derfor vil vi bestemme proporsjonene av massen av C i disse tre forbindelsene:

  • T2C: 1 gram c/2 gram t
  • TC: 2 gram c/2 gram t
  • T2C3: 3 gram c/2 gram t

Vi vil ha et forhold for massen av C lik 1: 2: 3. Det vil si at det er 2 ganger mer C i TC enn i T2C, og 3 ganger mer c i t2C3 enn i t2C. Som det kan sees, er 1: 2: 3 små hele tall (de overskrider ikke engang dusin).

Eksempler på loven med flere proporsjoner

For de følgende eksemplene vil de samme tidligere trinnene bli brukt, men vi vil ta hensyn til molmassene til de respektive elementene, forutsatt at en mol av forbindelsen.

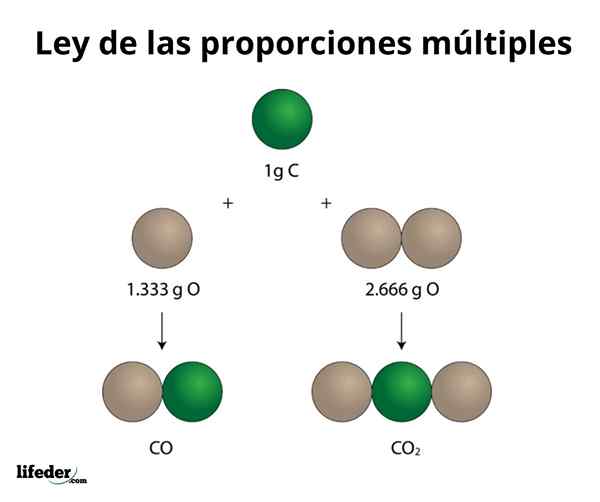
KOKOSNØTT2

Dette eksemplet forklarer på en enkel måte hvordan loven om flere proporsjoner fungerer; I CO (karbonmonoksid) er det 1.333 gram oksygen for hvert gram karbon. I karbondioksid (CO₂) er det 2.666 gram oksygen for hvert gram karbon. Derfor er andelen oksygen i begge forbindelser 1: 2, et lite heltallnummer.

H2ÅH2ENTEN2

Loven om flere proporsjoner gjelder paret av h2ÅH2ENTEN2.

Kan tjene deg: 30 eksempler på kjemiske suspensjoner

I en mol h2Eller, 2 gram hydrogen er kombinert med 16 gram oksygen. I mellomtiden, i en mol av h2ENTEN2, 2 gram hydrogen er kombinert med 32 gram oksygen. For å bekrefte om denne loven er oppfylt, må vi sette den samme massen for et av elementene i begge forbindelser. Denne gangen er hydrogen: 2 gram.

Masseforhold for h2Eller og h2ENTEN2 er:

  • H2O: 16 gram eller/2 gram h
  • H2ENTEN2: 32 gram eller/2 gram h

Forholdet mellom massen til O vil være 16:32. Imidlertid kan vi forenkle det ved å dele med 16, opphold 1: 2. Igjen er det endelige forholdet sammensatt av små hele tall.

SW2-SW3

I en mol av så2, 32 gram svovel er kombinert med 32 gram oksygen. I mellomtiden, i en mol av SO3, 32 gram svovel er kombinert med 48 gram oksygen. Svovelmassen er den samme for begge forbindelser, slik at vi direkte kan sammenligne oksygenforhold:

  • SW2: 32 gram eller
  • SW3: 48 gram eller

Å være forholdet mellom oksygenmassen mellom begge forbindelser som tilsvarer 32:48 eller 1: 1.5. Men var ikke der at det skulle være hele tall? Forhold 1: 1.5 (1/1.5) Det kan også skrives som 2: 3 (0.6), og igjen vil vi ha små hele tall: 2 og 3.

Merk at vi også kunne ha skrevet forholdet som 48:32 eller 1.5: 1, å være resultatet 3: 2. Loven endres ikke, bare tolkningen av forholdet: det er 1.5 eller 3/2 ganger mer oksygen i SO3 det i SO2; som er det samme å si at det er 2/3 eller 0.6 ganger mindre oksygen i SO2 det i SO3.

NEI NEI2-N2PÅ2ENTEN3-N2ENTEN5

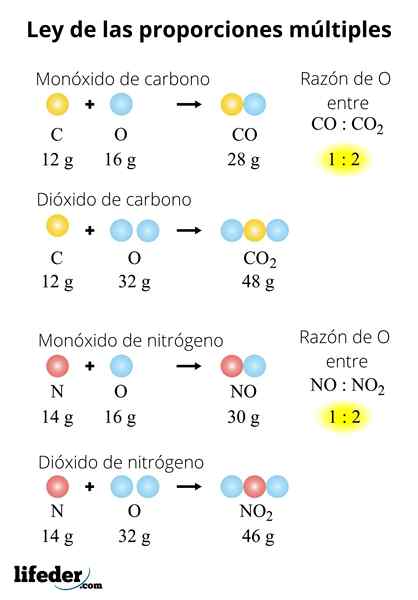
Loven kan også brukes på en serie forbindelser. Tenk på nitrogenoksider: ikke-ikke2-N2PÅ2ENTEN3-N2ENTEN5. For å evaluere denne loven i dem, må vi sette en masse nitrogen: 28 gram. Fordi? Fordi nei og nei2 De har et nitrogenatom mindre enn de andre oksydene:

  • 2 (nei): 28 gram n/32 gram eller
  • 2 (nei2): 28 gram n/64 gram eller
  • N2O: 28 gram n/ 16 gram eller
  • N2ENTEN3: 28 gram n/ 48 gram eller
  • N2ENTEN5: 28 gram n/ 80 gram eller
Det kan tjene deg: Hypofysesyre (H3PO2): Egenskaper, bruksområder og reagenser

La oss glemme nitrogen og fokusere på oksygengramene:

  • 2 (nei): 32 gram eller
  • 2 (nei2): 64 gram eller
  • N2O: 16 gram eller
  • N2ENTEN3: 48 gram eller
  • N2ENTEN5: 80 gram eller

Å være forholdet mellom massene på eller lik 32: 64: 16: 48: 80. For å forenkle det, deler vi alle tallene blant de minste, de 16, er som 2: 4: 1: 3: 5.

Det vil si at det er: 2 ganger mer oksygen i nei enn i n2Eller, 4 ganger mer oksygen i nei2 det i n2Eller, 3 ganger mer oksygen i n2ENTEN3 det i n2Eller, og 5 ganger mer oksygen i n2ENTEN5 det i n2ENTEN. Igjen har vi små hele tall, fra 1 til 5.

Begrensninger

Loven om flere proporsjoner er ikke alltid oppfylt. For eksempel er ikke molmassene eller atomvektene til elementene hele figurer, men har mange desimaler. Dette endrer de beregnede forholdene fullstendig, som slutter å være enkelt.

På samme måte er loven ikke oppfylt for tunge forbindelser, for eksempel noen hydrokarboner. For eksempel undecano, celleveH24, har 1.0083 eller 121/120 ganger mer hydrogen enn dekan, C10H22, hvis forhold er sammensatt av 121 og 120, som overstiger dusin; De er ikke små hele tall.

Og til slutt mislykkes loven med ikke -støkiometriske forbindelser, som med mange oksider og sulfider.

Konklusjon

Loven om flere proporsjoner sier at når to elementer danner mer enn en forbindelse, er de forskjellige massene av et element som kombineres med den samme massen av det andre elementet i en andel av et lite tall.

Referanser

  1. Whitten, Davis, Peck & Stanley. (2008). Kjemi. (8. utg.). Cengage Learning.
  2. Wikipedia. (2020). Lov om flere proporsjoner. Hentet fra: i.Wikipedia.org
  3. Redaktørene av Enyclopaedia Britannica. (2020). Lov om flere proporsjoner. Gjenopprettet fra: Britannica.com
  4. Chemistrygod. (4. juni 2019). Lov om flere proporsjoner av Dalton. Gjenopprettet fra: Chemistrygod.com
  5. Garcia Nissa. (2020). Lov om flere proporsjoner: Definisjon og eksempel. Studere. Gjenopprettet fra: Studie.com