Matte

De Morgan Laws

De Morgan Laws

Vi forklarer hva Morgan's lover er, vi demonstrerer dem og setter eksempler

Figur 1.- Matematikeren Augustus of Morgan (1806-1871) og hans lover om proposisjonell logikk. Kilde: f. Zapata.

Hva er De Morgan's lover?

De Morgan's lover er to logiske lover som tilhører den proposisjonelle logikken som ble formulert av den engelske matematikeren Augustus of Morgan (1806-1871). De etablerer følgende, med hensyn til en sammensatt logisk forslag:

  1. Det motsatte av en konjunksjon tilsvarer disjunksjonen som er dannet med motsetningene eller fornektelsene av forslagene som utgjør konjunksjonen.
  2. Nektelse av disjunksjon kan uttrykkes som en forbindelse som består av motsetningene eller fornektelsene av forslagene som er involvert i disjunksjonen.

I notasjonen av proposisjonell logikk kommer De Morgan's lover uttrykt på en kompakt og mer formell måte som dette:

  1. ∼ (P ∧ Q) ⇔ ∼P ∨Q
  2. ∼ (P ∨ Q) ⇔ ∼P ∧Q

Det disse lovene uttrykker er at resultatet, enten i fornektelsen av konjunksjon eller disjunksjon.

For en bedre forståelse av De Morgan's lover, er det nødvendig å gjennomgå betydningen av forslagene og symbolene som brukes i proposisjonell logikk, for å se hvordan disse lovene praktisk gjelder.

Logisk notasjon

Det grunnleggende verktøyet for proposisjonell logikk er proposisjonene. En logisk proposisjon er en uttalelse som innrømmer en reell verdi, Om det er sant eller usant, men ikke begge samtidig. I dette er ingen tvetydighet tillatt, det vil si at det ikke kan være tvil.

Et forslag er betegnet med en små bokstaver, som i følgende eksempler:

  • Spørsmål: Mexico City er hovedstaden i Mexico (sant).
  • Spørsmål: Ved å legge til 2 og 3, 4 (falsk) oppnås.
  • A: Alle pattedyr er landdyr (usant).
Kan tjene deg: heptagon

Det er også mer komplekse proposisjoner, som er strukturert ved bruk av enkle proposisjoner, slik som disse:

  • Q: Carlos vil gå på kino hvis det ikke regner.
  • Spørsmål: Ana er en kjemiker eller marinbiolog.
  • A: Juan skal på middag eller Pedro vil se spillet på TV.

Logiske kontakter

Logiske kontakter er symboler som brukes til å koble enkle proposisjoner og dermed bygge mer komplekse proposisjoner. I proposisjonell logikk har hver av dem en spesiell betydning.

De mest brukte kontaktene er konjunksjon, disjunksjon, eksklusiv disjunksjon, fornektelse, betingelse og bi-kondisjonalitet.

Konjunksjon

Konjunksjonen er betegnet med et omvendt "V" -brev. Et sammensatt forslag gjennom en konjunksjon symboliseres p ∧ q, som følger:

  • P ∧ Q: Mexico City er hovedstaden i Mexico og er i Nord -Amerika.

Det er lett å identifisere her at P er "Mexico City er hovedstaden i Mexico" og Q er "er i Nord -Amerika".

Disjunksjon

To typer disjunksjon utmerker seg: de svake og eksklusive. EN svak disjunksjon Det symboliseres av ∨ og i logisk notasjon ville det være P ∨ q. Eksempel på denne typen disjunksjon er:

  • P ∨ Q: Juan er en fotballspiller eller Juan er en tennisspiller.

I stedet Eksklusiv disjunksjon Det symboliseres med tegn ⊻ og innebærer at en av forslagene må utelukkes, for eksempel:

P ⊻ Q: Alicia er 20 år gammel eller Alicia er 22 år gammel.

Forskjellen mellom begge typer er tydelig, i eksklusiv disjunksjon, er et av forslagene utelukket, siden hvis Alicia er 20 år gammel, kan han ikke være 22 og omvendt. På den annen side, i den svake disjunksjonen, kan Juan være en fotballspiller og tennisspiller samtidig.

Benektelse

Ved å sette symbolet ∼ et forslag, nektes dette, som i:

  • Spørsmål: ∼ (Veracruz er hovedstaden i Mexico).

Som blir lest som "Veracruz er ikke hovedstaden i Mexico". Andre måter å uttrykke en fornektelse på, bortsett fra "nei", er gjennom setninger som "er falsk", "det er en løgn som" og "det er ikke sant at".

Kan tjene deg: lineær interpolasjon

Betingelse

De er sammensatte proposisjoner som vanligvis bruker ordene "ja" og "da ..." for å koble to proposisjoner der det er betingelse eller implikasjon. Den delen av forslaget som er skrevet umiddelbart etter "ja" er forutgående bølge hypotese av forslaget og hva som er etter begrepet "da" er konklusjon enten konsekvent.

Symbolet som brukes til betingelse er pilen fra venstre til høyre "→", derfor er en betingelse mellom to proposisjoner representert som P → Q, som kan leses som "hvis P, deretter Q". For eksempel:

P → Q: Hvis det regner i løpet av ettermiddagen, vil jeg ikke spille tennis.

Bi-kondisjonalitet

I denne typen proposisjoner blir uttrykket "ja, og bare hvis" for å koble sammen to proposisjoner, kalt første og andre biconditional -medlem, brukt. Symbolet som brukes er den toveispilen "↔".

De to proposisjonene koblet gjennom "ja, og bare hvis" kalles henholdsvis først og Andre medlem og bi-conditionaliteten til to proposisjoner p og q forblir som p ↔ q. For eksempel:

P ↔ Q: Maria liker å sykle hvis og bare hvis dagen er solrik.

Demonstrasjon av De Morgan's lover

De Morgan's lover er en del av logiske ekvivalenser og kan demonstreres gjennom sannhetstabellene, som brukes til å vite sannheten (sann eller falsk) verdi av et forslag.

Siden konjunksjonen bare er sant når P og Q er sann, er sannhetstabellen:

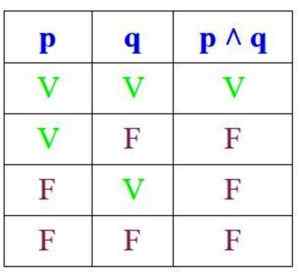
På den annen side, i disjunksjon, er proposisjonen sant hvis P og Q er sant, eller hvis minst en av dem er, men det er usant hvis begge er:

Kan tjene deg: Permutasjoner uten repetisjon: Formler, demonstrasjon, øvelser, eksempler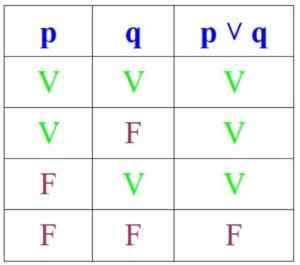

Nå forvandler fornektelse sannheten til falsk og omvendt. I dette tilfellet er sannhetsverdiene til ∼ (P ∧ Q) og ∼ (P ∨ Q) det motsatte av sannhetsverdiene (P ∧ Q) og (P ∨ Q):

Og det må verifiseres at disse resultatene oppnås når du utfører de respektive sannhetstabellene til (∼ P ˅ ∼ Q) og (∼ P ˄ ∼ Q):

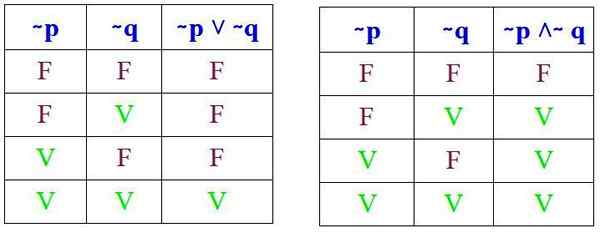
Og når du sammenligner de respektive sannhetstabellene, observeres det at De Morgan's lover er oppfylt. Nå vil to eksempler på dens anvendelse bli sett.

Løst eksempel 1

Bruk De Morgan's lover for å finne det tilsvarende uttrykket: ∼ (∼P ˅ ∼Q)

  • Løsning

Det gitte uttrykket sammenlignes ∼ (∼P ˅ ∼Q) med Morgan's lov:

∼ (P ∨ Q) ⇔ ∼P ∧Q

Og det observeres at fornektelsen allerede er utenfor parentesen i begge tilfeller, derfor følges instruksjonene i loven: den nekter ∼P, nekter ∼Q og kontakten endres:

∼ (∼P ˅ ∼q) ⇔ ∼ (∼P) ∧ ∼ (∼q) ⇔ P ∧ q

Løst eksempel 2

Bestem det ekvivalente uttrykket av ∼ [∼P ˄ ∼ (∼q)] ≡

  • Løsning

For det første er ∼Q -avslaget forenklet:

∼ [∼P ˄ ∼ (∼q)] ⇔ ∼ [∼P ˄ Q]

Siden det allerede er et fornektelse utenfor braketten, blir det resulterende uttrykket sammenlignet med Morgan's lov: ∼ (P ∧ Q) ⇔ ∼P ∨Q

For å løse ∼ [∼P ˄ Q] må du nekte ∼P, nekte Q og endre kontakten:

∼ [∼P ˄ Q] ⇔∼ (∼P) ∨ ∼Q ⇔ P ˅ ∼Q

Referanser

  1. Becerra, J.M.  UNAM -logikknotater.
  2. Strålende. Fra Morgan's lover. Gjenopprettet fra: strålende.org.
  3. Elektroniske opplæringsprogrammer. Av Morgan's teorem. Gjenopprettet fra: elektronikk-tormales.Ws.
  4. López, f. Introduksjon til matematisk logikk. Gjenopprettet fra: YouTube.com
  5. Muñoz, ca. Introduksjon til logikk. Hentet fra: Nettsteder.UCM.er.