Fermat -grense hva som består og øvelser løst

Han Fermat -grense Det er en numerisk metode som brukes for å oppnå verdien av skråningen til en linje, som er tangent til en spesifikk funksjon av dets domene. Det brukes også til å oppnå kritiske punkter for en funksjon. Hans uttrykk er definert som:

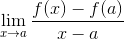
Det er åpenbart at Fermat ikke kjente grunnlaget for avledningen, men det var studiene hans som fremmet en gruppe matematikere for å forhøre seg om tangente linjer og deres anvendelser i beregningen.

[TOC]

Hva er Fermats grense?

Den består av en tilnærming på 2 punkter, som under tidligere forhold danner en sikringslinje til funksjonen med kryssing i par av verdier.

Når du nærmer deg variabelen til "A" -verdien, er punktene forpliktet til å møte. På denne måten blir den tidligere tørkelinjen tangent til punktet (a; f (a)).

Kvotientverdien (x - a), når den blir evaluert i punkt “a”, kaster en ubestemmelse av type K -grenser mellom null (k/0). Hvor disse ubestemmelsene kan brytes gjennom forskjellige faktoriseringsteknikker.

De mest brukte operasjonsteknikkene er:

-Firkantet forskjell (a² - b² ) = (a + b) (a - b); Eksistensen av elementet (A-B) innebærer i mye av tilfellene den faktoren som forenkler uttrykket (X-A) i Fermat-grenseforholdet.

- Firkantet fullføring (øks² + bx); Etter å ha fullført firkanter oppnås en Newton Binomial, der en av de to faktorene er forenklet med uttrykket (x - a), og bryter ubestemmelsen.

- Konjugat (a + b) / (a ​​+ b); Multipliser og dele uttrykket med konjugatet til en viss faktor kan være til stor hjelp for å bryte ubestemmelsen.

- Fellesfaktor; I mange tilfeller er resultatet av å betjene telleren til fermat f (x) - f (a) gjemt til faktoren (x - a) nødvendig for å faktorisere. For dette observeres det nøye hvilke elementer som gjentas i hver faktor av uttrykket.

Fermat Limit -søknad for maksimum og minimum

Selv når Fermats grense ikke skiller mellom maksimum og minimum.

Basekunnskap om den grafiske teorien om funksjoner som er i samsvar med dette teoremet, kan være tilstrekkelig til å etablere maksimale og minimumsverdier mellom funksjoner. Faktisk kan bøyningspunkter defineres av teoremet om den ekstra gjennomsnittsverdien til Fermats teorem.

Den kubiske lignelsen

Det mest betydningsfulle paradokset for Fermat kom når du studerte den kubiske lignelsen. Fordi hans oppmerksomhet var rettet mot tangentlinjene i en funksjon for et gitt punkt, møtte han problemet med å definere nevnte tangentlinje på det eksisterende bøyningspunktet i funksjonen.

Det virket umulig å bestemme tangentlinjen til et punkt. Dermed begynner henvendelsen som vil gi opphav til differensialberegningen. Deretter definert av viktige eksponenter for matematikk.

Maximus og minimous

Studien av maksimum og minimum en funksjon var en utfordring for klassisk matematikk, der en utvetydig og praktisk metode for definisjonen av disse.

Fermat opprettet en metode basert på driften av små differensialverdier, som etter faktoriseringsprosesser er eliminert ved å vike for mest og minimal verdi.

Denne variabelen må evalueres i det opprinnelige uttrykket for å bestemme koordinaten til nevnte punkt, som sammen med analytiske kriterier vil bli definert av det maksimale eller minimum av uttrykket.

Metode

I sin metode bruker Fermat Vietas bokstavelige symbolikk, som besto av eksklusiv bruk av store bokstaver: vokalene, for de ukjente og konsonantene for de kjente mengdene.

Når det uendelig mellom uendelig.

Denne prosessen består av å dele hvert uttrykk med den forskjellige verdien som brukes. Når det.

Historie

Fermats grense er faktisk et av de minst anerkjente bidragene i matematikerens lange liste. Studiene hans var fra primtall, for i utgangspunktet å lage basene for beregning.

På sin side var Fermat kjent for sine eksentrisiteter angående hypotesene hans. Det var vanlig for en slags utfordring for datidens andre matematikere, da han allerede hadde løsningen eller demonstrasjonen.

Det hadde et stort utvalg av tvister og allianser med forskjellige matematikere av tiden, som elsket eller hater å jobbe med ham.

Hans siste teorem var hovedansvaret for hans verdensberømmelse, der han sa at en generalisering av Pythagoras teorem For enhver "n" grad var det umulig. Sies å ha en gyldig demonstrasjon av det, men døde før du offentliggjorde det.

Denne demonstrasjonen måtte vente cirka 350 år. I 1995 endte matematikerne Andrew Wiles og Richard Taylor, angsten av Fermat som ble igjen, og demonstrerte at han hadde rett gjennom en gyldig demonstrasjon av sitt siste teorem.

Øvelser

Oppgave 1

Definer skråningen på linjen tangent til kurven f (x) = x² På punktet (4, 16)

Erstatte i uttrykket av fermat -grensen du har:

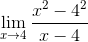
Bruk av kvadratimimumsnummer telleren er faktor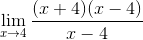

Faktorene er forenklet (x - 4)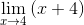

Når du evaluerer du har

M = 4 + 4 = 8

Oppgave 2

Definer det kritiske uttrykkspunktet f (x) = x² + 4x ved hjelp av Fermat -grensen

I dette tilfellet er det ingen koordinat, så x -verdien erstattes av den generiske skjemaet x₀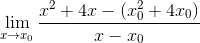

En strategisk gruppering av elementer utføres, og søker å gruppere X-X-jevnaldrende₀

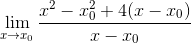
Torg er utviklet

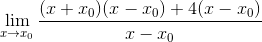
Den vanlige faktoren X-X er observert_{0 og blir trukket ut}

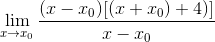
Uttrykket kan allerede forenkles og ubestemmelse er ødelagt

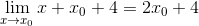
I minimumspunktene er det kjent at skråningen på tangentlinjen er lik null. På denne måten kan vi matche null uttrykket funnet og fjerne x -verdien₀    

2 x₀ + 4 = 0

X₀ = -4/2 = -2

For å få den manglende koordinaten trenger du bare å evaluere punktet i den opprinnelige funksjonen

F (-2) = (-2)² + 4 (-2) = 4 - 8 = - 4

Det kritiske poenget er P (-2, -4).

Referanser

1. Ekte analyse. En historisk tilnærming Sauhl Stahl, John Wiley & Sons, 5. august. 1999.
2. Den matematiske karrieren til Pierre av Fermat, 1601-1665: Second Edition. Michael Sean Mahoney. Princeton University Press, 5. juni. 2018
3. Fra Fermat til Minkowski: Forelesninger om teorien om tall og dens historiske utvikling. W. Scharlau, h. Opolka, Springer Science & Business Media, 1985
4. Fermats siste teorem: En genetisk introduksjon til algebraisk tallteori. Harold m. Edwards. Springer Science & Business Media, 14. januar. 2000
5. Fermat Days 85: Matematikk for optimalisering. J.-B. Hiriart-Urusty Elsevier, 1. januar. 1986