Størrelsesorden for å klatre på hva det består av, egenskaper og eksempler

EN Skalarstørrelse Det er en numerisk mengde hvis bestemmelse bare krever kunnskap om dens verdi med hensyn til en viss måleenhet av samme art. Noen eksempler på skalærstørrelser er avstand, tid, masse, energi og elektrisk ladning.

Skalarstørrelsene er generelt representert med en bokstav eller med symbolet på absolutt verdi, for eksempel TIL eller ǀTILǀ. Størrelsen på en vektor er en skalær størrelse og kan oppnås matematisk ved algebraiske metoder.

På samme måte er skalare mengder representert grafisk med en rett linje med en viss lengde, uten spesifikk retning, relatert til en skalafaktor.

[TOC]

Hva er en skalær størrelse?

I fysikk er en skalær mengde en fysisk størrelse representert av en fast numerisk verdi og en mønsterenhet, som ikke avhenger av referansesystemet. Fysiske størrelser er matematiske verdier relatert til målbare fysiske egenskaper til et objekt eller fysisk system.

Hvis du for eksempel vil få hastigheten på et kjøretøy, i km/t, bare del avstanden som er tilbakelagt mellom den forløpte tiden. Begge mengder er numeriske verdier ledsaget av en enhet, derfor er hastigheten en skalær fysisk størrelse. En skalær fysisk størrelse er den numeriske verdien av en målbar fysisk egenskap uten en spesifikk veiledning eller betydning.

Ikke alle fysiske størrelser er klatremengder, noen uttrykkes ved hjelp av en vektor som har numerisk verdi, retning og mening. For eksempel, hvis du vil få hastigheten på kjøretøyet, må forskyvningene som er gjort i løpet av tiden som er gått, bestemmes.

Disse forskyvningene er preget av å ha en numerisk verdi, en spesifikk retning og betydning. Følgelig er kjøretøyets hastighet en fysisk størrelse i vektor så vel som forskyvning.

Kjennetegn på en skalær størrelse

-Det er beskrevet med en numerisk verdi.

-Operasjoner med skalærstørrelser styres av grunnleggende algebra -metoder som sum, subtraksjon, multiplikasjon og inndeling.

-Variasjonen av en skalærstørrelse avhenger bare av endringen i dens numeriske verdi.

-Det er representert grafisk med et segment som har en spesifikk verdi assosiert i en måleskala.

Det kan tjene deg: Gasekonstant: Hva er, beregning og eksempler

-Skalarfeltet gjør det mulig å bestemme den numeriske verdien av en fysisk størrelse å klatre på hvert punkt i det fysiske rommet.

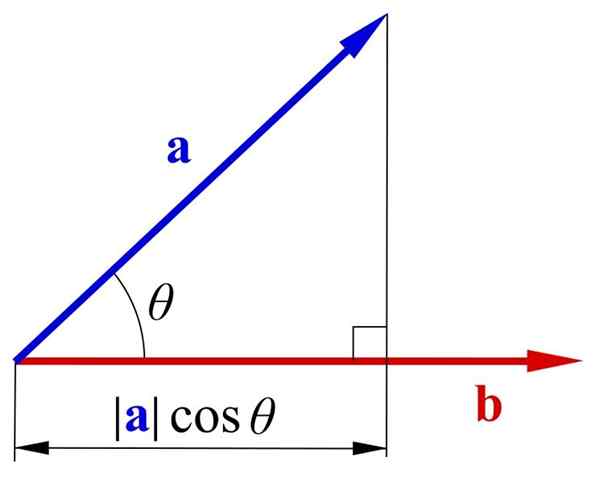
Skalarprodukt

Skalarproduktet er et produkt av to vektorstørrelser multiplisert med kosinien i vinkelen θ som dannes sammen. Når skalarproduktet av to vektorer beregnes, er resultatet som er oppnådd en skalærstørrelse.

Scalar -produktet av to vektorstørrelser til og b er:

til.b = ǀaǀǀbǀ.cosθ = ab.Cos θ

til= Det er den absolutte verdien av vektoren til

b= Absolutt verdien av vektoren b

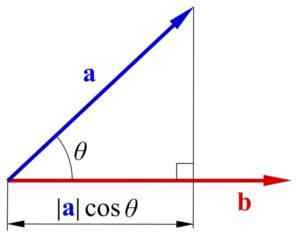Produkt av to vektorer. Av SVJO (https: // Commons.Wikimedia.org/wiki/fil: skalar-dot-produkt-1.Png)

Skalærfelt

Et skalarfelt er definert ved å knytte til hvert punkt i rom eller region en skalærstørrelse. Med andre ord, skalarfeltet er en funksjon som viser en posisjon for hver skalarstørrelse innenfor rommet.

Noen eksempler på skalærfelt er: temperaturen på hvert punkt på jordoverflaten på et øyeblikk, det topografiske kartet, feltet med gasstrykk, belastningstettheten og det elektriske potensialet. Når skalarfeltet ikke er avhengig av tid, kalles det det stasjonære feltet

Ved grafisk å representere settet med feltpunkter som har samme skalarstørrelse, dannes utstyret. For eksempel er utstyret til spesifikke elektriske belastninger konsentriske sfæriske overflater sentrert på belastningen. Når en elektrisk ladning beveger seg rundt overflaten er det elektriske potensialet konstant på hvert punkt på overflaten.

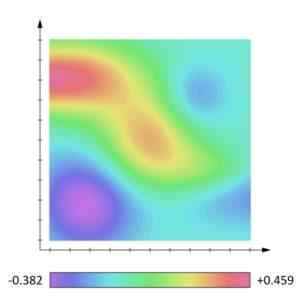Trykkstiltak Skalarfelt. [Av Lucas V. Barbosa (https: // Commons.Wikimedia.org/wiki/fil: scalar_field.Png)]

Eksempler på skalærstørrelser

Noen eksempler på skalærstørrelser som er fysiske egenskaper for naturen er nevnt nedenfor.

Temperatur

Det er den gjennomsnittlige kinetiske energien til partiklene til et objekt. Det måles med et termometer og verdiene oppnådd i målingen er skalare mengder forbundet med hvor varmt eller hvor kaldt objekt er.

Lengde

Lengden består av dimensjonen til et objekt som vurderer utvidelsen i en rett linje. Målsenheten som brukes i det internasjonale systemet med enheter (SIU) er T -banen og er betegnet med bokstav M.

Kan tjene deg: konkav speil

Tid

En av de vanligste bruksområdene er tid. Kan måles på sekunder, minutter og timer. Det er en styrke som brukes til å måle intervallet der hendelser oppstår.

For eksempel er varigheten av en fotballkamp 90 minutter.

Press

Trykket er en skalær fysisk størrelse som måler kraften i den vinkelrette retningen per overflateenhet. Målsenheten som brukes er Pascal og er betegnet med stavelsen PA eller bare for bokstaven P.

Et eksempel er miljøpresset, som er vekten som luftmassen i atmosfæren utøver på ting.

Energi

Energi er definert som materiens evne til å handle kjemisk eller fysisk. Målsenheten som brukes er Joules (Joule) og er betegnet med bokstav J.

Masse

For å oppnå massen til en kropp eller gjenstand, er det nødvendig å telle så mange atompartikler, molekyler som den besitter, eller måle hvor mye materiale objektet integrerer. En verdi av massen kan oppnås for å veie objektet med en balanse, og det er ikke nødvendig å etablere kroppens orientering for å måle dens masse.

Volum

Det er assosiert med det tre -dimensjonale rommet okkupert av et legeme eller stoff. Det kan måles i liter, milliliter, kubikkcentimeter, kubiske desimeter blant andre enheter og er en skalær mengde.

Hastighet

Målingen av hastigheten på et objekt i kilometer i timen er en skalærstørrelse, det er bare nødvendig å etablere den numeriske verdien av objektruten som en funksjon av den forløpte tiden.

Elektrisk ladning

Protonene og nøytronene til de subatomære partiklene har elektrisk ladning som manifesteres av den elektriske styrken til tiltrekning og frastøtning. Atomer i sin nøytrale tilstand har nullelektrisk ladning, det vil si at de har den samme numeriske verdien av protoner som nøytroner.

Energi

Energi er et tiltak som kjennetegner en kroppens evne til å utføre en jobb. På grunn av det første prinsippet om termodynamikk, er det fastslått at energi i universet forblir konstant, ikke blir skapt eller ødelagt bare transformeres til andre former for energi.

Kan tjene deg: optiske egenskaper til materialer

Elektrisk potensial

Det elektriske potensialet når som helst i rommet er den elektriske potensielle energien per belastningsenhet, det er representert med utstyrsoverflater. Potensiell energi og elektrisk ladning er skalare mengder, derfor er det elektriske potensialet en skalær mengde og avhenger av verdien av belastningen og det elektriske feltet.

Tetthet

Det er målet på mengden av masse av kropp, partikler eller stoffer i et visst rom og uttrykkes i masseenheter etter volumenheter. Den numeriske verdien av tettheten oppnås, matematisk, som deler massen mellom volumet.

Lysstyrke

Den lysende intensiteten er den lysende fluksen i en viss retning, utstrålt av en solid vinkelenhet. Målsenheten er stearinlyset, betegnet med CD -skjemaet.

Mer daglig, lysintensitet er det som kalles glans. Dette er til stede i objekter som en pære, en telefon eller et hvilket som helst objekt som avgir lys.

Mengde stoff

Målsenheten som brukes til å måle mengden stoff er molen. Dette er en veldig viktig skalarstørrelse innen kjemi.

Én mol inneholder partikkelavogadro -nummeret, og dens masse er atom- eller molekylmasse uttrykt i gram.

Frekvens

Frekvensen er antall ganger eller repetisjoner av et fenomen eller periodisk hendelse, utført i en bestemt tidsenhet. Målsenheten som brukes for denne skalære størrelsesorden er Hertz eller Hercio og er betegnet med bokstavene Hz.

For eksempel kan en ung person lytte til lyder mellom kl. 20.00 og 20.000 Hz. Når lyden forlater det bandet, kan ikke folk oppfatte det.

Referanser

1. Spiegel, M R, Lipschutz, S og Spellman, D. Analysevektor. s.l. : Mc Graw Hill, 2009.
2. Muvdi, B B, Al-Khafaji, A W og MC NABB, J W. Statistikk for ingeniører. VA: Springer, 1996.
3. Merkevare, l. Analysevektor. New York: Dover Publications, 2006.
4. Griffiths, D J. Introduksjon til elektodynamikk. New Jersey: Prentice Hall, 1999. p. 1-10.
5. Tallack, J C. Introduksjon til vektoranalyse. Cambridge: Cambridge University Press, 2009.