Vektet gjennomsnitt hvordan det beregnes, eksempler og øvelser

De Vektlagt gjennomsnitt eller vektet aritmetisk middel, det er et sentralt tendensmål der, til hver x -verdi_Yo som kan ta en variabel x, er en peso p tilordnet_Yo. Som et resultat ved å betegne det vektede gjennomsnittet med x_p, Du har:

Med summeringen av summen er formelen for det vektede gjennomsnittet:

Der n representerer mengden verdier valgt fra variabel x.

P_Yo, som også kalles vektingsfaktor, Det er et mål på viktigheten som forskeren tildeler hver verdi. Denne faktoren er vilkårlig og alltid positiv.

I dette at det vektede gjennomsnittet skiller seg fra det enkle aritmetiske gjennomsnittet, for i dette, hver av verdiene x_n Det har lik betydning. I en rekke applikasjoner vurderer forskeren muligens at noen verdier er viktigere enn andre og vil tildele en vekt i henhold til kriteriene deres.

Her er det mest kjente eksemplet: Anta at en student presenterer N -evalueringer i ett emne, og alle har samme vekt i den endelige lappen. I dette tilfellet, for å beregne den endelige merknaden, vil det være nok til å lage et enkelt gjennomsnitt, det vil si legg til alle kvalifikasjonene og dele resultatet med n.

Men hvis hver aktivitet har en annen vekt, fordi noen evaluerer viktigere eller mer komplekst innhold, vil det være nødvendig å multiplisere hver evaluering med deres respektive vekt, og deretter legge til resultatene for å oppnå den endelige vurderingen. Vi får se hvordan du utfører denne prosedyren i delen av løste øvelser.

[TOC]

Eksempler

Figur 1. Det vektede gjennomsnittet brukes ved beregning av forbrukerprisindeksen, en inflasjonsindikator. Kilde: Pxhere.

Eksemplet på kvalifikasjonene beskrevet ovenfor er et av de mest typiske når det gjelder anvendelse av det vektede gjennomsnittet. En annen veldig viktig anvendelse innen økonomi er konsumprisindeks enten Forbrukerens prisindeks IPC, også kalt Familiekurv Og det fungerer som en inflasjonsevaluerer i en økonomi.

Kan tjene deg: vinkler og trekanter

I sin utdyping tas en serie gjenstander i betraktning som mat og alkoholfrie drikkevarer, klær og fottøy, medisiner, transport, kommunikasjon, utdanning, fritid og andre varer og tjenester.

Eksperter tildeler hvert felt en vektingsfaktor, i henhold til deres betydning i folks liv. Prisene blir samlet inn i en etablert tidsperiode, og med all informasjonen beregnes IPC for nevnte periode, som kan være månedlig, bimonthly, halvårlig eller årlig, for eksempel.

Massesenteret i et partikkelsystem

I fysikk har det vektede gjennomsnittet en viktig applikasjon, som skal beregne Massesenteret av et partikkelsystem. Dette konseptet er veldig nyttig når du jobber med et utvidet organ, der dets geometri skal tas i betraktning.

Massesenteret er definert som punktet der hele massen til et utvidet objekt er konsentrert. På dette punktet kan kreftene påføres som vekt, for eksempel, og dermed forklare deres bevegelser av oversettelse og rotasjon, gjennom de samme teknikkene som de fungerte når alle objekter skulle være partikler.

Ved enkelhet begynner det å anta at det utvidede legemet er sammensatt av et beløp N av partikler, hver av dem med masse m og sin egen beliggenhet i verdensrommet: Koordinatpunktet (x_Yo, og_Yo, z_Yo).

Være x_CM Koordinaten x Fra CM sentrum, da:

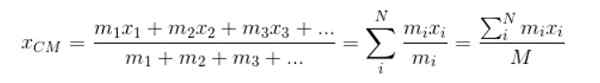
M representerer den totale massen i systemet. Fortsetter på samme måte for å finne koordinatene og_CM og z_CM:

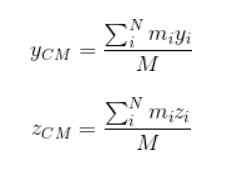
Vektfaktoren i dette tilfellet er massen til hver av partiklene som utgjør det utvidede objektet.

Kan tjene deg: Transcendente funksjoner: Typer, definisjon, egenskaper, eksempler

Viktige egenskaper ved massesenteret

Når antall partikler er veldig stort, er det et kontinuerlig objekt. I dette tilfellet er n → ∞ og summen erstattet av et definert integral, hvis grenser er gitt av objektstørrelsen.

Det er viktig å fremheve det faktum at det ikke nødvendigvis er masse på massesenterets beliggenhet. For eksempel i en smultring smultring, sammenfaller massesenteret mer eller mindre med det geometriske sentrum av Rosquilla.

Figur 2. Massesenteret til en smultring, et ganske symmetrisk objekt, er i hullet. Kilde: Pixabay.

Plasseringen av massesenteret avhenger ikke av referansesystemet som brukes til å etablere partiklene, siden det er en egenskap som avhenger av selve objektkonfigurasjonen og ikke hvordan den sees fra forskjellige referanserammer.

Løste øvelser

- Oppgave 1

I mange tilfeller tildeler lærere forskjellige vekter eller prosenter til hver evalueringsaktivitet i stolen. Således har for eksempel oppgavene en prosentandel, de andre forskjellige eksamenene og slutten -av -år -eksamen en sannsynligvis mye større.

Figur 3. I sine evalueringsplaner tildeler lærere vanligvis forskjellige vekter til evalueringer. Kilde: Karakterbok av David Mulder gjennom Flickr.

Anta at i et bestemt emne er evalueringsaktivitetene og deres respektive vekter følgende:

-Husoppgaver: 20 %

-Korte eksamener: 25 %

-Laboratorierapporter: 25 %

-Slutteksamen: 30 %

a) Hvordan beregner læreren den endelige karakteren til dette emnet for hver elev?

b) Anta at kvalifikasjonene til en bestemt student er, i skalaen 1 til 5, følgende:

-Oppgaver: 5.0 poeng

-Korte eksamener: 4.7 poeng

-Laboratorierapporter: 4.2 poeng

-Slutteksamen: 3.5 poeng

Det kan tjene deg: enegon: egenskaper, hvordan lage en enegon, eksempler

Finn den endelige merknaden til studenten i dette emnet.

Løsning

a) Hver evaluering har en annen vekt, som læreren har tildelt i henhold til deres kompleksitet og deres egne kriterier. På denne måten beregnes den endelige vurderingen direkte som:

Definitive = (x20 % oppgaver + korte eksamener x25 % + rapporter x25 % + avsluttende eksamen x30 %) / 100

b) definitive = (5.0 x 0.2) + (4.7 x 0.25) + (4.2 x 0.25) + (3.5 x 0.3) poeng = 4.275 poeng ≈ 4.3 poeng

- Oppgave 2

Eierne av en klesbutikk kjøpte jeans fra tre forskjellige leverandører.

De første solgte 12 enheter til en pris av € 15 hver, de andre 20 enhetene på 12.€ 80 hver og en tredje kjøpte mye fra 80 enheter på 11.€ 50.

Hva er gjennomsnittsprisen betalt av butikkeierne for hver cowboy?

Løsning

x_p = (12 x 15 + 20 x 12.80 +80 x 11.50) / (12+20+80) € = 12.€ 11

Verdien av hver cowboy er 12.€ 11, uavhengig av at noen koster litt mer og andre litt mindre. Det hadde vært nøyaktig det samme hvis eierne av butikken hadde kjøpt de 112 jeansene fra en enkelt leverandør som ville ha solgt dem i 12.€ 11 stykket.

Referanser

1. Arvelo, a. Målinger av sentral tendens. Hentet fra: Franarvelo.WordPress.com
2. Mendenhall, w. 1981. Statistikk for administrasjon og økonomi. 3. utgave. IBEROAMERICA REDAKSJON GROUP.
3. Moore, d. 2005. Grunnleggende statistikk anvendt. 2. Utgave.
4. Triola, m. 2012. Elementær statistikk. 11. Ed. Pearson Education.
5. Wikipedia. Vektlagt gjennomsnitt. Hentet fra: i.Wikipedia.org