Omtrentlig måling av amorfe figurer Eksempel og trening

De Omtrentlig måling Av de amorfe figurene består av en serie metoder som brukes for å bestemme området eller omkretsen av geometriske figurer som ikke er trekanter, firkanter, sirkler, etc. Noen kan utvides til tre -dimensjonale figurer.

I utgangspunktet består målingen av å lage et retikulat regelmessig, for eksempel rektangler, firkanter eller trapesoider, som dekker omtrent overflaten. Nøyaktigheten av tilnærmingen til området oppnådd ved disse metodene øker med finessen eller tettheten av retikulasjonen.

Figur 1. Steiner formet som amorfe figurer. Kilde: PXFuel.

Figur 1 og 2 viser forskjellige amorfe figurer. For å beregne området, er et retikulert, sammensatt av 2 x 2 firkanter, som igjen er delt inn i tjuefem firkanter på 2/5 x 2/5.

Å legge til områdene i hovedkvartene og de sekundære rutene det omtrentlige området av den amorfe figuren oppnås.

Figur 2. Et retikulat for å beregne området til en av de amorfe figurene på en omtrentlig måte. Kilde: f. Zapata

[TOC]

Område under en kurve

Det er ofte nødvendig å beregne området under en kurve mellom to grenseverdier. I dette tilfellet, i stedet for et firkantet retikulært, kan rektangulære striper spores omtrent området under nevnte kurve.

Summen av alle rektangulære striper kalles Riemanns sum eller sum. Figur 3 viser en partisjon av intervallet [a, b] som du vil bestemme omtrent området under kurven.

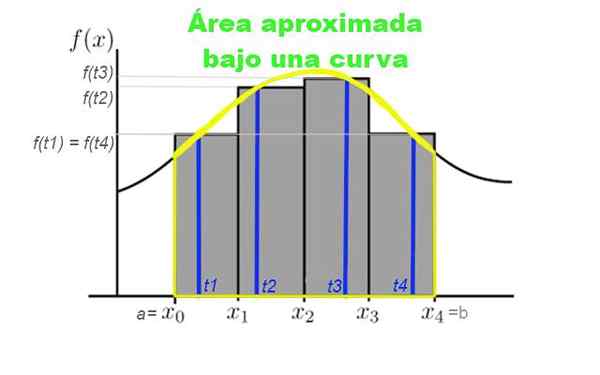Figur 3. Partisjon av intervallet [a, b] i fire underintervaler, som vanligvis er hentet fra samme bredde. Høyden på rektanglene bestemmes av verdien av kurven for en TK som tilhører underintervallene. Kilde: f. Zapata.

Anta at du vil beregne området under kurven gitt av funksjonen y = f (x), der x tilhører intervallet [a, b] som du vil beregne området. For dette er det laget en partisjon av N -elementer innenfor dette intervallet:

Kan tjene deg: 60 deling

Partisjon = x0 = a, x1, x2, ..., xn = b.

Deretter oppnås det omtrentlige området under kurven gitt av y = f (x) i intervallet [a, b] med følgende sum:

S = ∑_{K = 1}ⁿ f (t_k) (x_k - x_K-1)

Hvor t_k er mellom x_K-1 og x_k: x_K-1 ≤ t_k ≤ x_k .

Figur 3 viser summen av riemann av kurven y = f (x) i intervallet [x0, x4]. I dette tilfellet ble det gjort en partisjon av fire underintervaler og summen representerer det totale arealet for de grå rektanglene. 

Denne summen representerer en tilnærming til området under kurven F mellom abscissas x = x0 og x = x4.

Tilnærmingen til området under kurven forbedres i den grad antallet n av partisjoner er større, og har en tendens til å være nøyaktig området under kurven når tallet n Partisjoner har en tendens til uendelig. 

I tilfelle kurven er representert med en analytisk funksjon, er verdiene f (t_k) De beregnes evaluering av nevnte funksjon i verdiene t_k. Men hvis kurven ikke har et analytisk uttrykk, gjenstår følgende muligheter:

1. Nærme deg kurven med en funksjon, for eksempel et polynom.
2. Ta de kartesiske koordinatene til punktene der kurven blir oppfanget med linjene x = t_k.

Regelmessige intervaller

Avhengig av valg av TK -verdi i intervallet [x_k, x_K-1], kan summen overvurdere eller undervurdere den nøyaktige verdien av området under kurven for funksjonen y = f (x). Det mest tilrådelige er å ta TK -punktet der det manglende området er omtrent lik det gjenværende området, selv om det ikke alltid er mulig å ta et slikt valg.  

Kan tjene deg: Multiplikativ omvendt: Forklaring, eksempler, løste øvelser

Ta TK på slutten

Det mest praktiske er da å bruke regelmessige intervaller av bred Δx = (b - a)/n, hvor a og b er minimums- og maksimumsverdiene for abscissa, mens n er antall underavdelinger.

I så fall nærmer området under kurven seg ved:

Område = F (a+Δx)+f (a+2Δx)+…+f [a+(n-1] Δx+f (b)*Δx

I det forrige uttrykket ble TK tatt i høyre ende av undergrensen.

Ta TK i venstre ende

En annen praktisk mulighet er å ta TK -verdien i venstre ende, i hvilket tilfelle summen som tilnærmer området er uttrykt som:

Område = [F (a)+f (a+Δx)+…+f (a+(n-1) Δx)*Δx

TK som sentral verdi

I tilfelle TK velges som den sentrale verdien av den vanlige underintervallet av Δx bredde, er summen som tilnærmer området under kurven:

Område = [F (A+Δx/2)+F (A+3Δx/2)+…+F (B- Δx/2)]*Δx

Noen av disse uttrykkene har en tendens til den nøyaktige verdien i den grad antallet underavdelinger er vilkårlig stort, det vil si at Δx har en tendens til null, men i dette tilfellet er antallet av summen enormt stort med den påfølgende beregningskostnaden. 

Eksempel

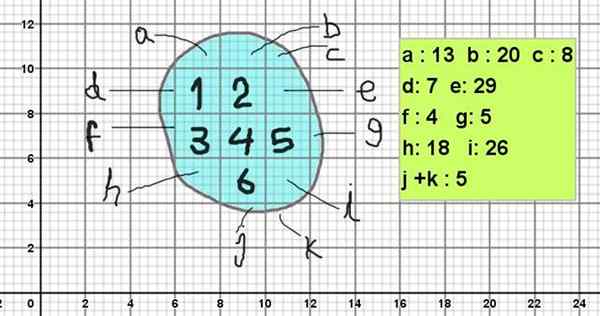
Figur 2 viser en amorf figur, hvis kontur er lik steinene i bilde 1. For å beregne arealet plasseres det på et retikulat med hovedtorg på 2 x 2 enheter til torget (for eksempel kan de være 2 cm²).

Og ettersom hver kvadrat er delt inn i 5 x 5 underavdelinger, har hver underavdeling et område på 0,4 x 0,4 kvadratmeter (0,16 cm²).

Figuren i figuren vil bli beregnet som følger:

Kan tjene deg: Vanlig faktorisering: eksempler og øvelser

Område = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0,16 cm²

Det er å si:

Område = 12 cm² + 135 x 0,16 cm² = 33,6 cm².

Trening løst

Beregn omtrent området under kurven gitt av funksjonen f (x) = x² Sats A = -2 opp til B = +2. For å gjøre dette, skriv summen for N vanlige partisjoner av intervallet [a, b] og ta deretter den matematiske grensen for saken at antall partisjoner har en tendens til uendelig. 

Løsning

For det første er partisjonsintervallet definert som 

Δx = (b - a)/n. 

Da er summen for høyre som tilsvarer funksjonen f (x) slik:

A = -2 og b =+2 erstattes slik at intervallet eller trinnet er Δx = 4/n. I dette tilfellet summen for funksjonen f (x) = x² er:

 Den firkantede binomialen er utviklet: 

[-2 +(4i/n)]² = 4 - 16 i /n + (4 /n)² Yo²

Og så erstattes den i summen:

Å skille summeringene og ta de konstante beløpene som en felles faktor for hver sum oppnås:

 Den første av summen, den andre er:

Og den tredje er:

Erstatte i uttrykket av summen du har:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

Når du velger en stor verdi for n, har du en god tilnærming til området under kurven. I dette tilfellet er det imidlertid mulig å oppnå den nøyaktige verdien som tar den matematiske grensen når n har en tendens til uendelig:

Område = lim_{N-> ∞}[16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²]

Område = 16 - (64/2)+ (64/3) = 16/3 = 5.333.

Referanser

1. Casteleiro, J. M. 2002. Omfattende beregning (Illustrated Edition). Madrid: ESIC -redaksjon.
2. Larson, r. 2010. Beregning av en variabel. 9na. Utgave. McGraw Hill.
3. Purcell, e. 2007. Beregning med analytisk geometri. 9na. Utgave. Pearson Education.
4. Unican. Historien om begrepet integral. Gjenopprettet fra: depot.Unican.er
5. UIS. Riemann summerer. Gjenopprettet fra: Matematikk.UIS.Edu.co
6. Wikipedia. Område. Gjenopprettet fra: er.Wikipedia.com