Variabilitetstiltak

Figur 1.- Den mest kjente variabilitetstiltakene. Kilde: f. Zapata.

Hva er variabilitetstiltak?

De Variabilitetstiltak, De er også kalt spredningstiltak, de er statistiske indikatorer som indikerer hvor nær eller fjerndata av dataene fra deres aritmetiske gjennomsnitt blir funnet. Hvis dataene er nær gjennomsnittet, er fordelingen konsentrert, og hvis de er langt, er det en spredt distribusjon.

Det er mange variabilitetstiltak, blant de mest kjente er:

• Område
• Gjennomsnittlig avvik
• Forskjell
• Standardavvik

Disse tiltakene kompletterer de sentrale tendensmålene og er nødvendige for å forstå fordelingen av dataene som er innhentet og trekke ut så mye informasjon som mulig.

Område

Rekkevidden eller ruten måler amplituden til et datasett. For å bestemme verdien, blir forskjellen mellom den høyeste verdien x funnet_Maks og minst x -verdien_min:

R = x_Maks - x_min

Hvis dataene ikke er løs, men gruppert etter intervall, beregnes området med forskjellen mellom den øvre grensen for det siste intervallet og den nedre grensen for det første intervallet.

Når området er en liten verdi, betyr det at alle dataene er ganske nær hverandre, men et stort område indikerer at det er mye variabilitet. Det er tydelig at området ikke tar hensyn til verdiene mellom dem, så det er ikke tilrådelig å bruke den når datanummeret er stort i den øvre grensen og den nedre grensen for dataene.

Imidlertid er det et øyeblikkelig tiltak å beregne og har de samme dataenhetene, så det er enkelt å tolke det.

Eksempel på rang

Deretter er listen tilgjengelig med antall mål merket i løpet av helgen, i fotballligaene fra ni land:

Kan tjene deg: hva er delingene av 30? (Forklaring)

40, 32, 35, 36, 37, 31, 37, 29, 39

Det er et datasett uten å gruppere. For å finne rekkevidden fortsetter de å bestille dem fra minst til største:

29, 31, 32, 35, 36, 37, 37, 39, 40

Dataene med den høyeste verdien er 40 mål, og den med den laveste verdien er 29 mål, derfor er rekkevidden:

R = 40-29 = 11 mål.

Det kan vurderes at området er lite sammenlignet med minimumsverdidataene, som er 29 mål, så det kan antas at dataene ikke har stor variabilitet.

Gjennomsnittlig avvik

Dette variabilitetsmålet beregnes gjennom gjennomsnittet av de absolutte verdiene for avvikene med hensyn til gjennomsnittet. Betegner gjennomsnittlig avvik som d_M, For ikke -grupperte data beregnes gjennomsnittlig avvik med følgende formel:

Hvor n er antall tilgjengelige data, x_Yo Det representerer hver data og x̄ er gjennomsnittet, som bestemmes ved å legge til alle dataene og dele mellom n:

Gjennomsnittsavviket gjør det mulig å vite i gjennomsnitt hvor mange enheter dataene avviker fra det aritmetiske gjennomsnittet og har fordelen av å ha de samme enhetene som dataene de fungerer.

Eksempel på mellomavvik

I henhold til dataene fra området er antallet mål som er merket:

40, 32, 35, 36, 37, 31, 37, 29, 39

Hvis du vil finne medium D -avviket_M Av disse dataene er det nødvendig å først beregne X̄ aritmetisk gjennomsnitt:

Og nå som verdien av X̄ er kjent, fortsetter vi å finne gjennomsnittlig avvik_M:

= 2.99 ≈ 3 mål

Derfor kan det sies at dataene i gjennomsnitt beveger seg omtrent i 3 gjennomsnittlige mål som er 35 mål, og som nevnt er det et mye mer presist tiltak enn rekkevidden.

Kan tjene deg: hyperbola

Forskjell

Gjennomsnittlig avvik er et mye tynnere variabilitetstiltak enn området, men som beregnet gjennom den absolutte verdien av forskjellene mellom hver data og gjennomsnittet, gir det ikke større allsidighet fra det algebraiske synspunktet.

Derfor er variansen foretrukket, som tilsvarer gjennomsnittet av den kvadratiske forskjellen på hver data med gjennomsnittet og beregnes ved å bruke formelen:

I dette uttrykket, S² betegner variansen, og som alltid x_Yo representerer hver av dataene, x̄ er gjennomsnittet og n totaldata.

Når du jobber med et utvalg i stedet for befolkningen, er det foretrukket å beregne variansen som dette:

Forskjellen med den forrige formelen er at det i nevneren er n - 1 i stedet for n. Det hender at ved å dele med n, undervurderer variansen av prøven variansen til befolkningen som den ble trukket ut fra, men ikke når den er delt på N - 1. I noen tekster vises uttrykket med navnet på Quasi-Variza.

I alle fall er varians preget av å alltid være en positiv mengde, men som gjennomsnittet av kvadratiske forskjeller, er det viktig å observere at den ikke har de samme enhetene som dataene.

Eksempel på varians

For å beregne variansen av dataene om eksemplene på rekkevidde og gjennomsnittlig avvik, erstattes de tilsvarende verdiene og den angitte summen. I dette tilfellet er det valgt å dele mellom n-1:

= 13.86

Standardavvik

Variansen har ikke samme enhet som for variabelen som studeres, for eksempel hvis dataene kommer i meter, resulterer variansen i kvadratmeter. Eller i eksemplet på målene det ville være i mål for mål, noe som ikke gir mening.

Kan tjene deg: Hva er elementene i lignelsen? (Deler)

Derfor er standardavviket definert, også kalt typisk avvik, Som kvadratroten av variansen:

S = √s²

På denne måten oppnås et mål på variabiliteten til dataene i de samme enhetene som disse, og jo lavere verdien av S, jo mer gruppert er dataene rundt gjennomsnittet.

Både variansen og standardavviket er variabilitetstiltakene som skal velges når det aritmetiske gjennomsnittet er målet for sentral tendens som best beskriver atferden til dataene.

Og det er at standardavviket har en viktig egenskap, kjent som Chebyshevs teorem: minst 75% av observasjonene er i intervallet definert av x̄ ± 2s. Med andre ord, 75% av dataene er på det meste i en avstand lik 2s rundt gjennomsnittet.

På samme måte er minst 89% av verdiene i en avstand på 3s fra gjennomsnittet, en prosentandel som kan utvides, forutsatt at mange data er tilgjengelige og disse følger en normalfordeling.

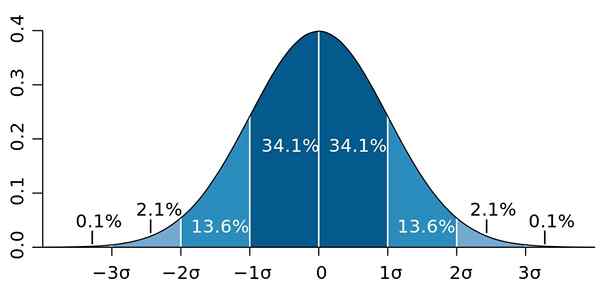
Figur 2.- Hvis dataene følger en normalfordeling, 95.4 av dem er to standardavvik på begge sider av gjennomsnittet. Kilde: Wikimedia Commons.

Eksempel på standardavvik

Standardavviket for dataene som presenteres i de foregående eksemplene er:

S = √s² = √13.86 = 3.7 ≈ 4 mål