Minst firkanter

Hva er metoden for minimumsplasser?

Metoden til Minst firkanter Det er en av de viktigste applikasjonene i tilnærmingen til funksjoner. Tanken er å finne en kurve slik at denne funksjonen, gitt et sett med ryddige par, blir bedre kontaktet til dataene. Funksjonen kan være en linje, en kvadratisk kurve, en kubikk osv.

Ideen med metoden er å minimere summen av kvadrater av forskjellene i ordinatene (komponent y), mellom punktene generert av den valgte funksjonen og punktene som tilhører datasettet.

Minimum kvadratmetode

Før vi gir metoden, må vi først være tydelige på hva "det nærmer seg". Anta at en linje er søkt y = b+mx som er den som best representerer et sett med n punkter, nemlig (x1, y1), (x2, y2) ..., (xn, yn).

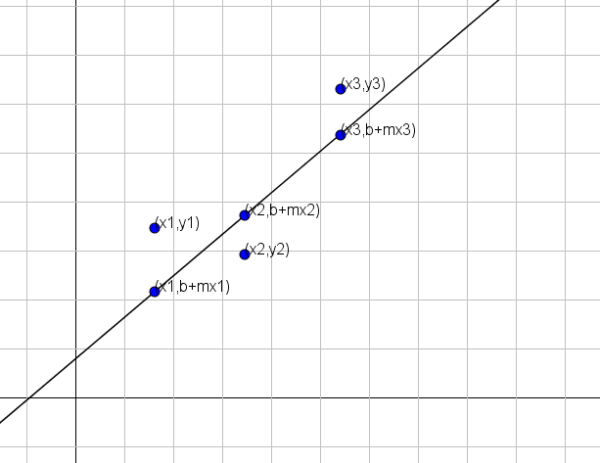
Som vist i forrige figur, hvis variablene x og y var relatert til linjen y = b+mx, ville for x = x1 den tilsvarende verdien av y være b+mx1. Imidlertid er denne verdien forskjellig fra den sanne verdien av y, som er y = y1.

Husk at i flyet er avstanden mellom to punkter gitt med følgende formel:

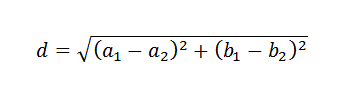
Med dette i bakhodet, for å bestemme hvordan du velger linjen y = b+mx som best nærmer seg de gitte dataene, høres det logisk ut som et kriterium valg av linjen som minimerer summen av rutene på avstandene mellom punktene og linjen.

Ettersom avstanden mellom punktene (x1, y1) og (x1, b+mx1) er y1- (b+mx1), reduseres problemet vårt til å finne tall m og b slik at neste sum er minimal:

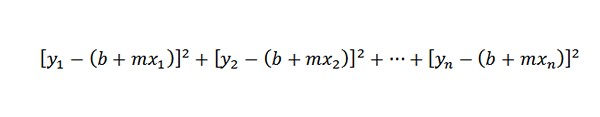
Linjen som oppfyller denne tilstanden er kjent som "tilnærmingen til linjen med minimumsplasser til punktene (x1, y1), (x2, y2), ..., (xn, yn)".

Når problemet er oppnådd, gjenstår det bare å velge en metode for å finne tilnærmingen ved minimumsplasser. Hvis punktene (x1, y1), (x2, y2), ..., (xn, yn) er alle på linjen y = mx+b, må vi være colineal og:

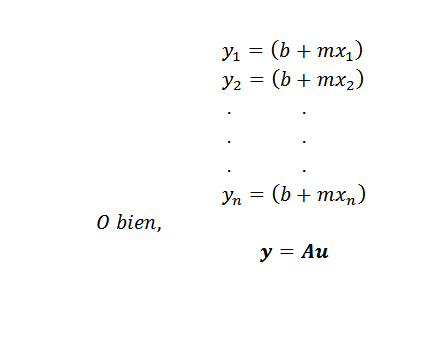
I dette uttrykket:

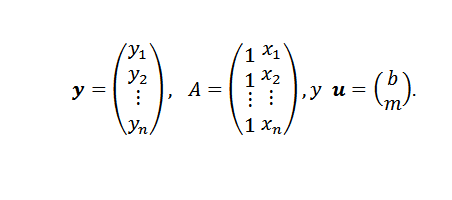
Til slutt, hvis punktene ikke er colineal, kan y-au = 0 og problemet oversette til å finne en vektor eller slik at den euklidiske standarden er minimal.

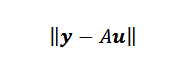
Å finne den minimerende vektoren eller er ikke så vanskelig som du kunne tro. Som en er en NX2 og U -matrise er en 2 × 1 matrise, vi har at AU -vektoren er en vektor i rⁿ og tilhører bildet av en, som er et underområde av rⁿ Med en dimensjon ikke mer enn to.

Vi vil anta at n = 3 for å vise hva som er prosedyren som må følges. Hvis n = 3, vil bildet av A være et fly eller en linje som passerer gjennom opprinnelsen.

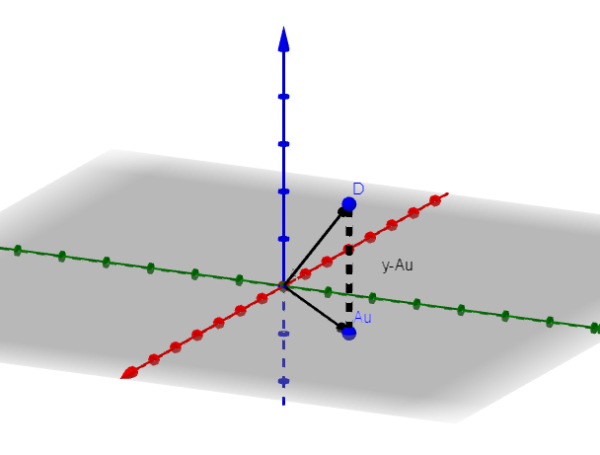
La V minimere vektoren. I figuren observerer vi at y-au minimeres når det er ortogonalt til bildet av en. Det vil si hvis V er minimeringsvektoren, så hender det at:

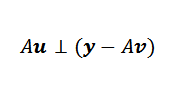
Deretter kan vi uttrykke det ovennevnte på denne måten:

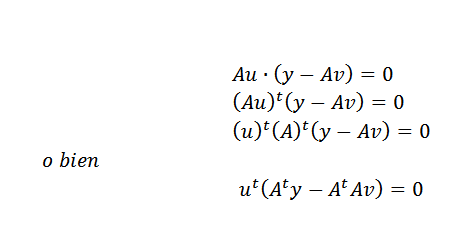
Dette kan bare skje hvis:

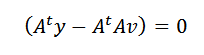
Til slutt, Clearing V, må vi:

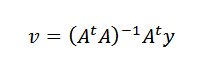
Det er mulig å gjøre dette siden^tA er inverterbare når n peker som data ikke er colineal.

Nå, i stedet for å lete etter en linje, ønsker vi å finne en lignelse (hvis uttrykk vil være av formen y = a+bx+cx²) At det var en bedre tilnærming til datapunktene, ville prosedyren bli beskrevet nedenfor.

Hvis datapunktene var i den lignelsen, måtte den:

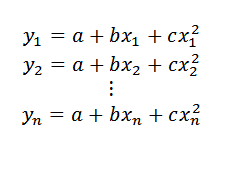
Deretter:

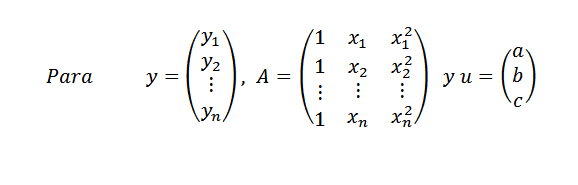
Tilsvarende kan vi skrive y = au. Hvis alle punktene ikke er i lignelsen, har vi at y-au er forskjellig fra null for en hvilken som helst vektor u, og problemet vårt er igjen: finn en vektor u i r3 slik at dens norm || y-au || være så mye som mulig.

Gjenta den forrige prosedyren, kan vi komme til Vector Wanted IS:

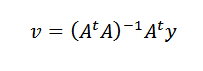
Løste øvelser

Oppgave 1

Finn linjen som best passer poengene (1.4), (-2.5), (3, -1) og (4.1).

Løsning

Vi må:

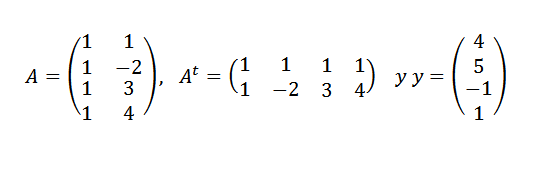
Deretter:

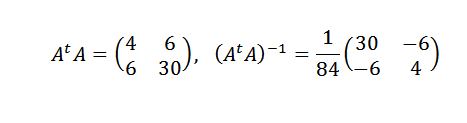
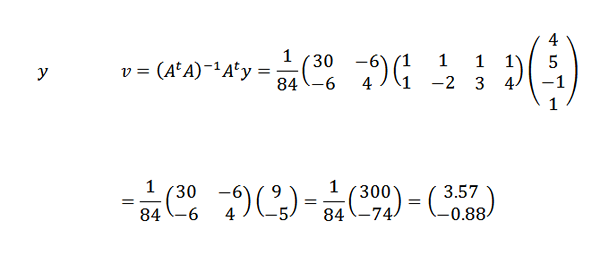
Derfor konkluderer vi med at linjen som passer best for poengene er gitt av:

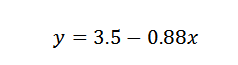
Oppgave 2

Anta at et objekt slippes fra en høyde på 200 m. Mens de faller, blir følgende tiltak iverksatt:

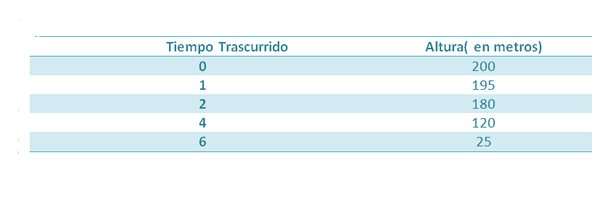
Vi vet at høyden på dette objektet, etter en tid er gått, er gitt av:

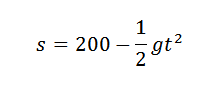
Hvis vi ønsker å oppnå verdien av G, kan vi se etter en lignelse som er en bedre tilnærming til de fem punktene som er gitt i tabellen, og dermed ville vi ha den koeffisienten som følger med t² Det vil være en rimelig tilnærming til (-1/2) g hvis målingene er nøyaktige.

Vi må:

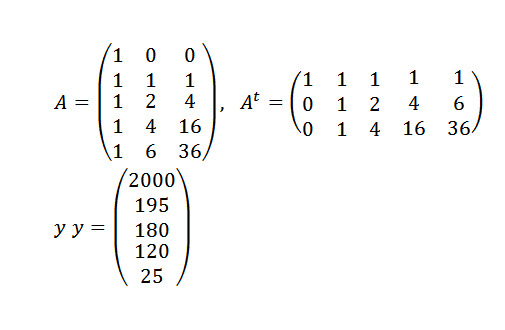
Og så:

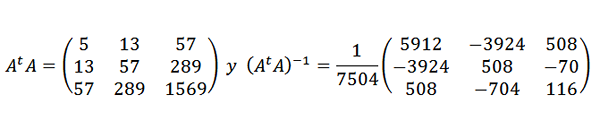
Så datapunktene blir justert av følgende kvadratiske uttrykk:

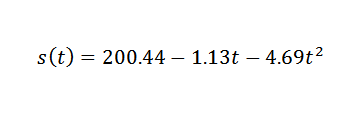
Så du må:

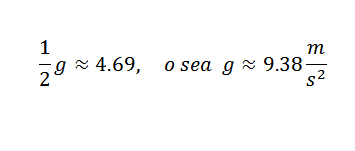
Dette er en verdi som er rimelig nær den riktige, som er G = 9,81 m/s². For å få en mer nøyaktig G av G ville det være nødvendig å starte fra mer presise observasjoner.

Hva er minimum kvadratmetode for?

I problemene som oppstår i natur- eller samfunnsvitenskap er det praktisk å skrive forholdet mellom forskjellige variabler gjennom noe matematisk uttrykk.

For eksempel kan vi relatere i økonomi kostnadene (c), inntekt (i) og fortjeneste (u) gjennom en enkel formel:

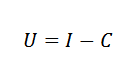
I fysikk kan vi relatere akselerasjonen forårsaket av tyngdekraften, tiden der et objekt har falt og høyden på objektet ved lov:

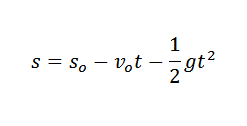
I forrige uttrykk S_enten Det er den første høyden på nevnte objekt og v_enten er din første hastighet.

Å finne formler som disse er imidlertid ikke en enkel oppgave; Det tilsvarer vanligvis den profesjonelle på plikt til å jobbe med mange data og utfører gjentatte ganger flere eksperimenter (for å bekrefte at resultatene som er oppnådd er konstante) for å finne sammenhenger mellom de forskjellige dataene.

En vanlig måte å oppnå dette på er å representere dataene som er oppnådd i et plan som punkter og søke en kontinuerlig funksjon som optimalt nærmer seg disse punktene.

En av måtene å finne funksjonen som "bedre tilnærminger" dataene som er gitt, er ved metoden for kvadratet minimum.

I tillegg, som vi også så i øvelsen, takket være denne metoden kan vi oppnå ganske nære tilnærminger til fysiske konstanter.