Bohr atommodell

Han Bohr atommodell Det er unnfangelsen av den danske fysikeren Niels Bohr (1885-1962) om atomets struktur, utgitt i 1913. I Bohr -atomet okkuperer elektroner rundt kjernen bare visse tillatte baner, takket være en begrensning som kalles kvantisering.

For Bohr, bildet av atomet som et miniatyr solsystem, med elektroner ved å kretsen rundt kjernen, var det ikke helt i samsvar med det faktum at elektriske ladninger, når de blir akselerert, utstråler energi.

Et atom som det ville ikke være stabilt, fordi det ville ende på å kollapse før eller siden fordi elektronene ville presipitere spiralt til kjernen. Og da for 50 år siden de karakteristiske lysmønstrene som avgir hydrogen og andre gasser når du oppvarmer.

Mønsteret eller spekteret består av en serie lyse linjer med visse veldig spesifikke bølgelengder. Og hydrogenatom kollapser ikke ved å avgi lys.

For å forklare hvorfor atomet er stabilt til tross for at han kunne utstråle elektromagnetisk energi, foreslo Bohr at vinkelmomentet bare kunne ta i bruk visse verdier, og derfor energien også. Dette er det som forstås ved kvantisering.

Å akseptere at energien ble kvantifisert, ville elektronet ha den nødvendige stabiliteten for ikke å skynde seg mot kjernen som ødela atomet.

Og atomet stråler bare lysenergi når elektronet gjør overganger fra en bane til en annen, alltid i diskrete mengder. På denne måten blir tilstedeværelsen av utslippsmønstre i hydrogen forklart.

Bohr komponerte på denne måten en visjon om atomet som integrerer kjente begreper av klassisk mekanikk med den nyoppdagede, for eksempel Plancks konstant, fotonet, elektronet, atomkjernen (Rutherford hadde vært en mentor av Bohr) og den nevnte spektra av problemstilling.

[TOC]

Hovedegenskaper ved Bohr -modellen

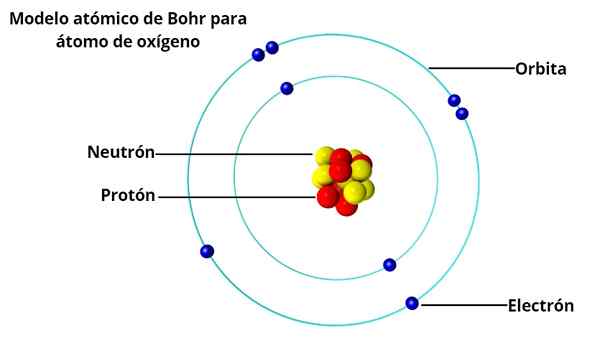
Bohrs atom. Animasjonen representerer elektronet når det går fra et høyere energinivå til en annen av mindre energi, og avgir et lys lys (et foton). Kilde: Wikimedia Commons.

Bohrs atommodell antar at elektronet beveger seg i en sirkulær bane rundt kjernen ved virkningen av den elektroniske attraksjonen til Coulomb og foreslår at elektronets vinkelmomentum er kvantisert.

Kan tjene deg: balanseringsvektor: beregning, eksempler, øvelser

La oss se hvordan du integrerer begge konseptene i matematisk form:

La l størrelsen på vinkelmomentet, m massen av elektronet, og hastigheten på elektronet og r radiusen til bane. Å beregne l vi har:

L = m⋅r⋅V

Bohr foreslo at L var lik hele multipler av konstanten H/2π, der H er Planck konstant, Introdusert for kort tid siden av fysikeren Max Planck (1858-1947) ved å løse energiproblemet som sendes ut av en svart kropp, et teoretisk objekt som absorberer alt det innfallende lyset.

Verdien er h = 6.626 × 10⁻³⁴ J ・ s, mens det ved h/2π er betegnet som ħ, Som lyder  "H bar".

Derfor gjenstår vinkelmomentet:

m⋅r⋅V = nħ, Med n = 1,2, 3 ..

Og fra denne tilstanden blir radioene til banene som er tillatt for elektronet trukket ut, som vi vil se da.

Elektronbaneralberegning

I det følgende vil vi anta de enkleste atomer: hydrogen, som består av et enkelt proton og et elektron, både med en størrelsesbelastning og.

Den sentripetale kraften som holder elektronet i sin sirkulære bane er gitt av elektrostatisk attraksjon, hvis størrelse f er:

F = ke²/r²

Hvor k er den elektrostatiske konstanten til Coulomb og R-loven, elektron-proteinavstanden. Å vite at i en sirkulær bevegelse_c Det er gitt av fornuft mellom kvadratet med hastighet og avstand r:

til_c = v² / r

Etter Newtons andre lov er nettokraften et produkt av masse m ved akselerasjon:

Mv²/r = ke²/r²

Forenkle radio R er oppnådd:

M⋅V²R = ke²

Ved å kombinere dette uttrykket med det fra vinkelmomentet har vi et ligningssystem, gitt av:

Det kan tjene deg: Fysisk bane: egenskaper, typer, eksempler og øvelser

1) MV²R = ke²

2) r = n ħ/mv

Tanken er å løse systemet og bestemme R, radius for den tillatte bane. En liten elementær algebra fører til svaret:

R = (nħ)² / K⋅m⋅e²

Med n = 1, 2, 3, 4, 5 ..

For n = 1 har vi det minste av radioene, kalt Bohr Radio a_enten Med en verdi på 0,529 × 10⁻¹⁰ m. Radioene til de andre banene kommer til uttrykk i form av til_enten.

På denne måten introduserer Bohr det viktigste kvantetallet n, påpeker at de tillatte radioene er basert på Planck -konstanten, den elektrostatiske konstanten og massen og belastningen på elektronet.

Bohr -atommodellen postulerer

Dansk fysiker Niels Bohr (1885-1962).

Bohr kombinerer dyktig Newtonsk mekanikk med de nye funnene som kontinuerlig hadde gitt i løpet av andre halvdel av 1800 -tallet og begynnelsen av 1900 -tallet. Blant dem det revolusjonerende begrepet "hvor mye", hvorav Planck selv hevdet ikke å være veldig overbevist om.

Gjennom sin teori kunne Bohr tilfredsstillende forklare serien med hydrogenspekteret og forutsi energiutslipp i rangering av det ultrafiolette og infrarøde, som ennå ikke var observert.

Vi kan oppsummere postulatene dine som følger:

Elektroner beskriver sirkulære bane

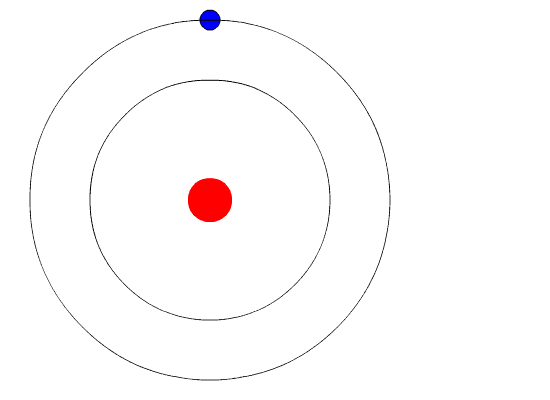
Elektronet dreier seg om kjernen i stabil sirkulær bane, med ensartet sirkulær bevegelse. Bevegelsen skyldes den elektrostatiske attraksjonen som kjernen utøver på den.

Vinkelmomentet er kvantifisert

Elektronets vinkelmomentum blir kvantifisert i henhold til uttrykket:

L = mvr = nħ

Hvor n er et heltall: n = 1, 2, 3, 4 ..., noe som fører til elektronet kan bare være i visse definerte baner, hvis radioer er:

R = (n ħ)² / k m e²

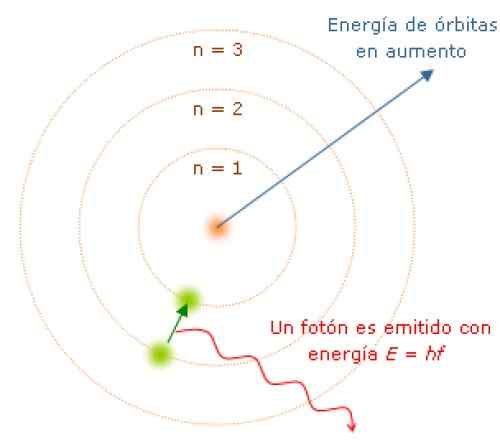
Elektroner avgir eller absorberer fotoner når de flytter fra en energitilstand til en annen

Når du går fra en energitilstand til en annen, absorberer eller avgir elektronet energi i diskrete mengder kalt fotoner. Kilde: Wikimedia Commons.

Siden vinkelmomentet er kvantisert, energi og også. Det kan demonstreres at E er gitt av:

Kan tjene deg: Vertikal skudd: Formler, ligninger, eksempler

Og erstatte alle konstanter er det oppnådd en forkortet form:

Voltelektronet eller EV, er en annen enhet for energi, mye brukt i atomfysikk. Det negative tegnet på energi sikrer at banenes stabilitet, som indikerer at arbeid bør gjøres for å skille elektronet fra denne posisjonen.

Mens elektronet er i sin bane ikke absorberer eller avgir lys. Men når det hopper fra en bane med større energi til en lavere en, gjør den det.

Frekvensen F av det utsendte lyset avhenger av forskjellen mellom energinivået til banene:

E = hf = e_første - e_endelig

Begrensninger

Bohr -modellen har visse begrensninger:

-Det gjelder bare hydrogenatom. Forsøk på å bruke det på mer komplekse atomer fungerte ikke.

-Det svarer ikke hvorfor noen baner er stabile og andre ikke. At energien i atomet ble kvantisert fungerte veldig bra, men modellen ga ikke en grunn, og det var noe som forårsaket ubehag for forskere.

-En annen viktig begrensning er at den ikke forklarte tilleggslinjene utstedt av atomer i nærvær av elektromagnetiske felt (Zeeman Effect and Stark Effect). Eller hvorfor noen spektrumlinjer var mer intense enn andre.

-Bohr -modellen vurderer ikke relativistiske effekter, som er nødvendig.

-Det tar for gitt at det er mulig å vite nettopp posisjonen og hastigheten til elektronet, men det som virkelig beregnes er sannsynligheten for at elektronet inntar en viss stilling.

Til tross for begrensningene, hadde modellen stor suksess den gangen, ikke bare for å integrere nye funn med allerede kjente elementer, men fordi den viste nye spørsmål, noe som gjorde det klart at veien til en tilfredsstillende forklaring av atomet var i kvantemekanikk.

Artikler av interesse

Schrödinger atommodell.

Broglie Atomic Model.

Chadwick Atomic Model.

Heisenberg Atomic Model.

Perrin Atomic Model.

Thomson Atomic Model.

Dalton Atomic Model.

Dirac Jordan Atomic Model.

Democritus Atomic Model.

Leucipo atommodell.

Sommerfeld Atomic Model.

Gjeldende atommodell.