Heltallstall

Hva er hele tall?

Hele tall utgjør et sett med nyttige tall for å telle de komplette objektene som har hatt og de som ikke er. Også for å telle de på den ene siden og den andre av et bestemt referansested.

Også med hele tallene kan subtraksjonen eller forskjellen utføres mellom et tall og et annet større enn ham, og for eksempel avgjort som en gjeld. Skillet mellom fortjeneste og gjeld gjøres med henholdsvis tegn + og -.

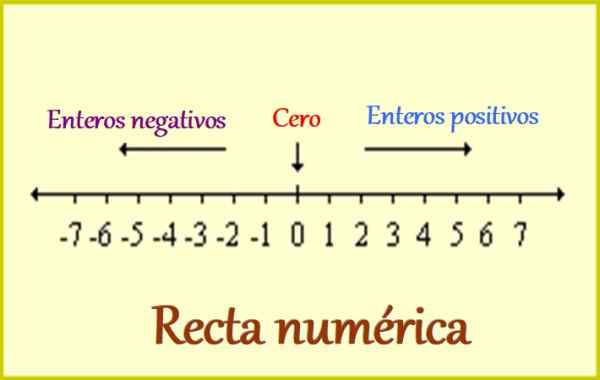
Figur 1. Den numeriske linjen for hele tall. Kilde: Wikimedia Commons. Leomg/CC By-SA (https: // CreativeCommons.Org/lisenser/by-SA/3.0).

Det er grunnen til at hele antallet inkluderer følgende:

-Positive heltall, som er skrevet foran med et +tegn, eller bare uten tegnet, siden det også er forstått at de er positive. For eksempel: +1, +2, +3 ... og så videre.

-0, der tegnet er irrelevant, fordi det ikke legger det til å trekke det fra noe beløp. Men 0 er veldig viktig, siden det er referansen for heltallene: på den ene siden er de positive plasseres og negativene, som vi ser i den øvre figuren.

-Negative heltall, som alltid må skrives fra tegnet -siden de med seg beløpene som gjeld og alle de som er på den andre siden av referansen, skilles. Eksempler på negative heltall er: -1, -2, -3 ... og fra da.

Hvordan er hele tall?

I begynnelsen representerer vi hele tallene med innstillingen av settet: z = … -4, -3, -2, -1, 0, +1, +2, +3, +4…, det vil si, oppført og organisert. Men en veldig nyttig representasjon er det som bruker den numeriske linjen. For dette er det nødvendig å trekke en linje, som vanligvis er horisontal, som 0 er merket og delt inn i identiske seksjoner:

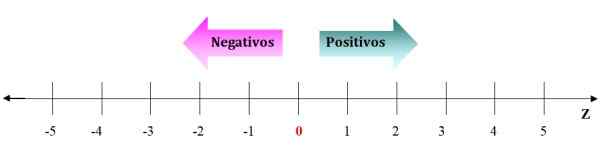Figur 2. Representasjon av hele tall på den numeriske linjen. Fra 0 til høyre er de positive heltallene og fra 0 til venstre negativene. Kilde: f. Zapata.

Negativene går til venstre for 0 og de positive går til høyre. Pilene på talllinjen symboliserer at tallene fortsetter å uendelig. Gitt noe hele antall, er det alltid mulig å finne et som er større eller annet enn det som er lavere.

Den absolutte verdien av et heltall

Den absolutte verdien av et heltall er avstanden mellom tallet og 0. Og avstandene er alltid positive. Derfor er den absolutte verdien av det negative heltallet antallet uten tegnet mindre.

For eksempel er den absolutte verdien på -5 5. Den absolutte verdien er betegnet med stenger, som følger:

| -5 | = 5

For å visualisere det, er det nok å ha mellomrommene på den numeriske linjen, fra -5 til 0. Mens den absolutte verdien av et positivt heltall er samme tall, for eksempel | +3 | = 3, siden avstanden til 0 er 3 mellomrom:

Kan tjene deg: Sandwich Law: Forklaring og øvelser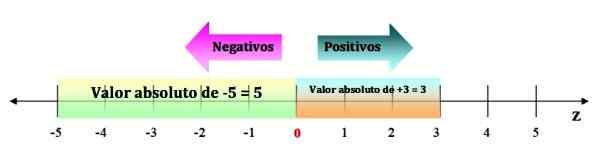Figur 3. Den absolutte verdien av et heltall er alltid en positiv mengde. Kilde: f. Zapata.

Egenskaper

-Settet med hele tall er betegnet som z og inkluderer settet med naturlige tall n, og elementene deres er uendelige.

-Et heltall og det som følger (eller det som går foran det) er alltid forskjellig i enheten. For eksempel etter at 5 kommer på 6, er det en forskjell mellom dem.

-Hvert hele nummeret har en forgjenger og en etterfølger.

-Ethvert positivt heltall er større enn 0.

-Et negativt heltall er alltid mindre enn 0 og at ethvert positivt antall. La oss for eksempel nummeret -100, dette er mindre enn 2, enn 10 og 50. Men det er også mindre enn -10, -20 og -99, og det er større enn -200.

-0 har ingen tegnshensyn, siden det ikke er negativt eller positivt.

-Med hele tallene kan de samme operasjonene som utføres med de naturlige tallene utføres, nemlig: sum, subtraksjon, multiplikasjon, potensiering og mer.

-Hele det motsatte av et visst heltall x, er -x og summen av et heltall med det motsatte er 0:

x + (-x) = 0.

Operasjoner med hele tall

- Addisjon

-Hvis tallene som skal legges til har samme tegn, blir deres absolutte verdier lagt til, og resultatet er plassert tegnet på at tilleggene har. Her er noen eksempler:

a) (+8) +( +9) = 8 +9 = +17

b) (-12) + ( - 10) = - (12 + 10) = -22

-I tilfelle at tallene er av forskjellige tegn, trekkes de absolutte verdiene (hovedfaget i mindreårige) og resultatet blir plassert tegnet på tallet med den høyeste absolutte verdien, som følger:

a) (-8) + (21) = 21 - 8 = 13

b) (-9) + (+4) = -(9-4) = -5

Egenskaper for summen av hele tall

-Summen er kommutativ, derfor endrer ikke rekkefølgen på summen summen. La A og B være to hele tall, det blir oppfylt at a+b = b+a

-0 er det nøytrale elementet i summen av hele tall: a + 0 = a

-Ethvert hele antall lagt til med det motsatte er 0. Det motsatte av + a er -a, og omvendt, det motsatte av -a es + a. Derfor: (+ a)+ (-a) = 0.

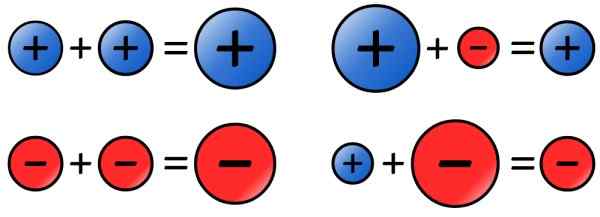Figur 4. Skilt regel for summen av hele tall. Kilde: Wikimedia Commons.

- Subtraksjon

For å trekke fra hele tall må du ledes av denne regelen: Subtraksjonen tilsvarer summen av et tall med det motsatte. La to nummer A og B, da:

A - b = a + (-b)

Anta for eksempel at du må utføre følgende operasjon: (-3) - (+7), da:

(-3) -(+7) = (-3)+( -7) = -(3+7) = -10

- Multiplikasjon

Multiplikasjonen av hele tall følger visse regler for tegnene:

-Produktet av to tall med Det samme tegnet Det er alltid positivt.

-Når to tall multipliserer forskjellige tegn, Resultatet er alltid negativt.

Kan tjene deg: Hva er delene av brøkdelen? (Eksempler)

-Verdien av produktet er lik å multiplisere de respektive absolutte verdiene.

Umiddelbart noen eksempler som tydeliggjør ovenstående:

(-5) x (+8) = -5 x 8 = -40

(-10) x (-12) = 10 x 12 = 120

(+4) x (+32) = 4 x 32 = 128

Egenskaper for multiplikasjon av hele tall

-Multiplikasjon er kommutativ. Være to hele tall A og B, det er sant at: a.b = b.A, som også kan uttrykkes som:

Rekkefølgen på faktorene endrer ikke produktet.

-Det nøytrale elementet i multiplikasjon er 1. Være for et heltall, derfor til.1 = 1

-Ethvert heltall multiplisert med 0 er lik 0: a.0 = 0

Distribusjonseiendom

Multiplikasjon oppfyller distribusjonseiendommer med hensyn til summen. Ja A, B og C er hele tall da:

til.(b +c) = a.b + a.c

Da et eksempel på hvordan du bruker denne eiendommen:

(-3). [(-4) + 11] = (-3).(-4)+(-3).11 = 12 -33 = 12 + (-33) = -21

Potensering

-Hvis basen er positiv, er resultatet av operasjonen alltid positivt.

-Når basen er negativ, hvis eksponenten er jevn, er resultatet positivt. Og hvis eksponenten er merkelig, er resultatet negativt.

- Inndeling

I divisjonen gjelder de samme tegnene for tegn som i multiplikasjon:

-Ved å dele to heltall med samme tegn, er resultatet alltid positivt.

-Når to heltall med forskjellige tegn er delt, er kvotienten negativ.

For eksempel:

(-12) ÷ (-4) = 3

33 ÷ (-3) = -11

Viktig: Divisjonen er ikke kommutativ, med andre ord til ÷ b ≠ b ÷ a og som alltid er ikke inndelingen mellom 0 tillatt.

- Potensering

Vær et helt tall og vi ønsker å heve det til en eksponent n, da må vi multiplisere av seg selv, som vist nedenfor:

tilⁿ = a.til.til.til.… til

La oss også vurdere følgende, med hensyn til at N er et naturlig tall:

-Hvis A er negativt og N er jevn, er resultatet positivt.

-Når A er negativ og N er merkelig, resulterer det i et negativt antall.

-Hvis A er positiv og N er jevn eller merkelig, er det alltid et positivt heltall.

-Ethvert heltall forhøyet til 0 er lik 1: a⁰ = 1

-Hvert tall høyt til 1 er lik antall: a¹ = a

La oss si for eksempel du vil finne (-3)⁴ , For å få den til å multiplisere (-3) fire ganger av seg selv, som dette: (-3).(-3).(-3).(-3) = 81.

Et annet eksempel, også med et negativt heltall er:

(-2)³ = (-2).(-2).(-2) = -8

Produkt av like base krefter

Anta at to krefter med lik base, hvis vi multipliserer dem, får vi en annen kraft med samme base, hvis eksponent er summen av de gitte eksponentene:

tilⁿ ·til^m = a^{n + m}

Lik basepulverforhold

Ved å dele krefter av samme base, er resultatet en kraft med samme base, hvis eksponent er subtraksjon av de gitte eksponentene:

Kan tjene deg: vinkler i omkretsen: typer, egenskaper, løste øvelser

tilⁿ ÷ a^m = a^{n - m}

Deretter to eksempler som tydeliggjør disse punktene:

(-2)³.(-2)⁵ = (-2) ³⁺⁵= (-2)⁸

5⁶ ÷ 5⁴ = 5^6-4 = 5²

Eksempler

La oss se på enkle eksempler for å anvende disse reglene, og huske at i tilfelle av positive heltall, kan tegnet dispenseres med:

a) (+6) + (+14) = 6 + 14 = 20

b) (-8) + ( - 10) = - (8 + 10) = -18

c) (-16) + (+7) = -16 + 7 = -9

d) (+4) + (-8) + (-25) = [(+4) + (-8)] + (-25) = [4-8] -25 = -4 -25 = -29

e) (-8) -( + 15) = (-8) + (-15) = -8 -15 = -23

f) (+3) x (+9) = 3 x 9 = 27

g) (- 4) x (-11) = 4 x 11 = 44

h) (+5) x (-12) = -5 x 12 = -60

i) (-2)³ = (-2) x (-2) x (-2) = -8

Løste øvelser

- Oppgave 1

En maur beveger seg på talllinjen i figur 1. Starter fra punkt x = +3 utfører følgende forskyvninger:

-7 enheter beveger seg til høyre

-Nå returneres 5 enheter til venstre

-Gå 3 enheter til venstre.

-Den kommer tilbake og flytter 4 enheter til høyre.

På hvilket tidspunkt er myren på slutten av ruten?

Løsning

La oss kalle forskyvningene. Når de er til høyre, får de et positivt tegn, og når de er på venstre negativt skilt. På denne måten, og starter fra x = +3 har du:

-Først D: x₁ = +3 +7 = +10

-Andre D: x₂ = +10 +(-5) = +5

-Tredje D: x₃ = +5 +(-3) = +2

-Fjerde D: x₄ = +2 +4 = +6

Når mauren slutter, er turen i stillingen x = +6. Det vil si at det er 6 enheter til høyre for 0 på den numeriske linjen.

- Oppgave 2

Løs følgende operasjon:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)]

Løsning

Denne operasjonen inneholder tegn på gruppering, som er parentes, firkantede parenteser og nøkler. Når du løser, må du ta vare på parentesene først, etter de firkantede parentesene og til slutt nøklene. Med andre ord, du må jobbe fra innsiden og ut.

I denne øvelsen representerer poenget en multiplikasjon, men i tilfelle mellom ett tall og en parentes eller annet symbol er det ikke noe poeng, på samme måte som det forstås at det er et produkt.

Deretter fungerer oppløsningen trinn for trinn, fargene fungerer som en guide for å følge resultatet av reduksjon av parenteser, som er de mest interne gruppesymbolene:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)] =

= 36 + [- (-16)].-[-6+ 5- (0)]+ 2 (-2)] =

= 36 + [16].-[-1] -4] =

= 52.1- 4] = 52.-3 = -156

- Øvelse 3

Løs den første gradslikningen:

12 + x = 30 + 3x

Løsning

Begrepene er gruppert med det ukjente til venstre for likhet, og de numeriske vilkårene til høyre:

x - 3x = 30 - 12

- 2x = 18

X = 18 / (-2)

x = - 9