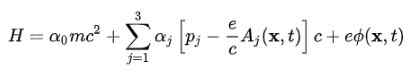Aomisk modell av Dirac Jordan -egenskaper og postulater

Han Dirac-Jordan Atomic Model Det er den relativistiske generaliseringen av den Hamiltonian operatøren i ligningen som beskriver kvantebølgefunksjonen. I motsetning til den foregående modellen, Schrodinger, er det ikke nødvendig å pålegge spinnet gjennom Paulis eksklusjonsprinsipp, siden det vises naturlig.

I tillegg inkluderer Dirac-Jordan-modellen relativistiske korreksjoner, spinnorgan-interaksjon og Darwins begrep, som står for den fine strukturen til de elektroniske nivåene i atomet.

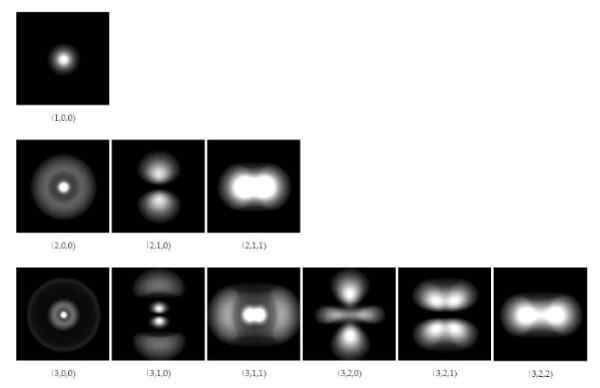
Figur 1. Elektroniske orbitaler i hydrogenatom for de tre første energinivåene. Kilde: Wikimedia Commons.

Fra 1928 var forskere Paul a. M. Dirac (1902-1984) og Pascual Jordan (1902-1980), ble foreslått å generalisere kvantemekanikken utviklet av Schrodinger, for å inkludere korreksjonen av Einsteins spesielle relativitet.

Dirac del av Schrodinger -ligningen, som består av en differensialoperatør, kalt Hamiltonian, som opererer på en funksjon kjent som Elektronbølgefunksjonen. Schrodinger tok imidlertid ikke hensyn til de relativistiske effektene.

Bølgefunksjonsløsninger tillater å beregne regionene der elektronet rundt kjernen vil bli funnet med en viss grad av sannsynlighet. Disse regionene eller områdene kalles Orbitaler Og de er avhengige av visse diskrete kvantetall, som definerer elektronens energi og vinkelmomentum. 

[TOC]

Postulater

I kvantemekaniske teorier, enten det er relativistisk eller ikke, er det ikke noe begrep om baner, siden verken posisjonen eller hastigheten på elektronet kan spesifiseres samtidig. Og i tillegg fører det til å spesifisere en av variablene til total upresisjon i den andre.

Hamiltonian er for sin del. For eksempel har et gratis elektron total energi, og det avhenger av det lineære momentumet p dermed:

E = (p²)/ 2m

For å bygge Hamiltonian, starter det fra dette uttrykket og erstattes p Av kvanteoperatøren for fart: 

p = -I ħ ∂ /∂r 

Det er viktig å merke seg at vilkårene p og p De er forskjellige, siden den første er fart og den andre er den Differensiell operatør assosiert med momentum. 

Kan tjene deg: Atomic Model of Leukipo: Postulater, Begrensninger, betydning

I tillegg er jeg den imaginære enheten og ħ Planck -konstanten delt med 2π, på denne måten den Hamiltonian operatøren h for det frie elektronet oppnås:

H = (ħ²/2m) ∂² /∂r² 

For å finne Hamiltonian av elektronet i atomet, tilsettes elektroninteraksjonen med kjernen: 

H = (ħ2/2m) ∂² /∂r²  - Eφ (r)

I det forrige uttrykket er elektronelektrisk ladning og φ (r) det elektrostatiske potensialet produsert av den sentrale kjernen.

Nå virker operatør H på bølgefunksjonen ψ i henhold til Schrodinger -ligningen, som er skrevet slik:

H ψ = (i ħ ∂ /∂t) ψ

De fire postulatene av Dirac

Første postulat: Den relativistiske bølgeforlikningen har samme struktur som Schrodingers bølgelikning, hva endrer seg er H:

H ψ = (i ħ ∂ /∂t) ψ

Andre postulat: Hamiltonian-operatøren er bygget basert på Einsteins energimomentum-forhold, som er skrevet slik:

E = (m² c⁴ + p² c²)^1/2

I det forrige forholdet, hvis partikkelen har momentum p = 0, har du den berømte ligningen E = MC² som relaterer hvilerenergien til enhver masse av masse m med lysets hastighet C.

Tredje postulat: For å få den Hamiltonian operatøren brukes den samme kvantiseringsregelen som ble brukt i Schrodinger -ligningen:

p = -I ħ ∂ /∂r

I begynnelsen var det ikke klart hvordan han skulle håndtere denne differensialoperatøren som virker innenfor en kvadratrot, så Dirac satte seg for å få en lineær Hamiltonian -operatør i momentumoperatøren og derfra oppsto hans fjerde postulat.

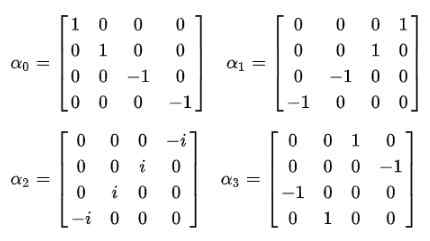
Postulat Room: For å bli kvitt kvadratroten i den relativistiske energiformelen, foreslo Dirac følgende struktur for E²:

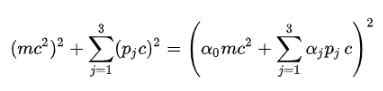
Selvfølgelig er det nødvendig å bestemme alfakoeffisientene (α0, α1, α2, α3) slik at dette blir oppfylt.

Dirac -ligningen

Dirac -ligningen ble først hevet for det frie elektronet, ved bruk av strukturen som ble foreslått i fjerde postulat. Det forblir som følger: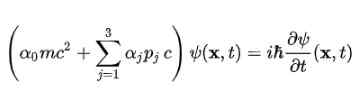

Det kan tjene deg: Hør kraft: overflate- og massekrefter

I sin kompakte form regnes Dirac -ligningen som en av de vakreste matematiske ligningene i verden:

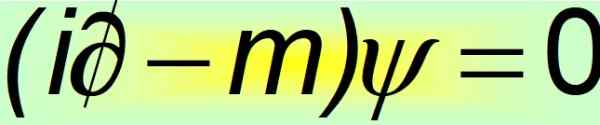Figur 2. Dirac ligning kompakt. Kilde: f. Zapata.

Og det er når det bevises at de konstante Alfas ikke kan være skalare mengder. Den eneste måten likheten i fjerde postulat er oppfylt på er at de er 4 × 4 konstante matriser, som er kjent som Dirac -matriser:

Det observeres umiddelbart at bølgefunksjonen slutter å være en skalarfunksjon og blir en fire -komponentvektor Espinor:

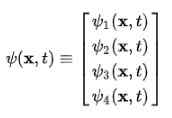
Dirac-Jordans atom

For å oppnå atommodellen er det nødvendig å bevege seg fra den frie elektronligningen til elektronet i det elektromagnetiske feltet produsert av atomkjernen. Denne interaksjonen tas i betraktning ved å inkorporere den potensielle skalaren φ og den potensielle vektoren TIL På Hamiltonian:

Bølgefunksjonen (Espinor) som er resultatet av å innlemme denne Hamiltonian har følgende egenskaper: 

- Det oppfyller den spesielle relativiteten, siden den tar hensyn til elektronets egen energi (første periode av den relativistiske Hamiltonian)

- Den har fire løsninger som tilsvarer de fire komponentene i Espinor

- De to første løsningene tilsvarer den ene til spinn +½ og den andre til spinnet - ½ 

- Til slutt forutsier de to andre løsningene eksistensen av antimaterie, siden de tilsvarer den for positronene til motsetninger motsetninger.

Den store fordelen med Dirac -ligningen er at de grunnleggende Hamiltonian korreksjonene av Schrodinger H (O) kan deles inn i flere begreper som vi vil vise nedenfor:

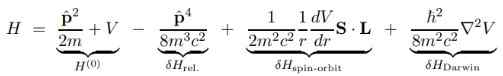
I det forrige uttrykket er V den potensielle skalaren, siden den potensielle vektoren TIL Det er ugyldig hvis det er ment å være den sentrale stasjonære protonen, og det er derfor det ikke vises.

Årsaken til at Diracs korreksjoner angående Schrodinger -løsninger i bølgefunksjonen er subtil. De oppstår fra det faktum at de tre siste begrepene i den korrigerte Hamiltonian alle er delt på hastigheten C på torget, et enormt tall, noe som gjør disse begrepene numerisk små.

Det kan tjene deg: Vy Canis Majoris: oppdagelse, egenskaper, struktur, trening og evolusjon

Relativistiske korreksjoner til energispekteret

Ved bruk av DIC-Jordan-ligningen blir korreksjoner funnet for elektronenergispekteret i hydrogenatomet. Det er også korreksjoner for energi i atomer med mer enn ett elektron omtrent gjennom en metodikk kjent som teorien om forstyrrelser.

Tilsvarende lar Dirac -modellen deg finne korreksjon av fin struktur ved hydrogenenerginivået. 

Imidlertid oppnås enda mer subtile korreksjoner som den hyperfine strukturen og lamets skift fra mer avanserte modeller som for eksempel Campos kvanteteori, født nettopp på grunn av bidragene fra Dirac -modellen.

Følgende figur viser hvordan Diracs relativistiske korreksjoner er på energinivå:

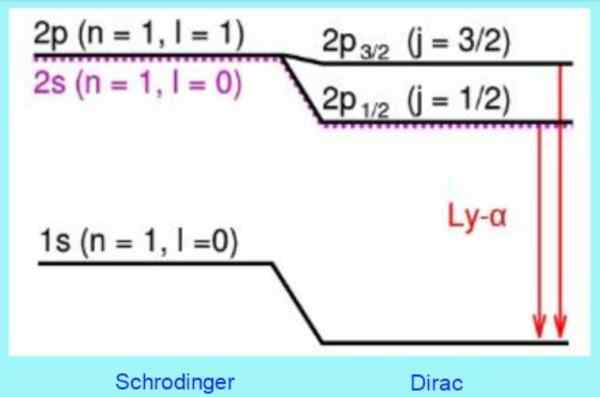Figur 3. Dirac -modellkorreksjoner ved hydrogenatomnivåer. Kilde: Wikimedia Commons.

For eksempel forutsier løsningene på Dirac -ligningen riktig et skifte observert på nivå 2s. Det er den velkjente finstrukturkorreksjonen i Lyman -linjen - Alfa of the Hydrogen Spectrum (se figur 3).

Forresten er den fine strukturen navnet som mottar atomfysikk utfoldet av linjene i emisjonsspekteret til atomene, som er en direkte konsekvens av det elektroniske spinnet.

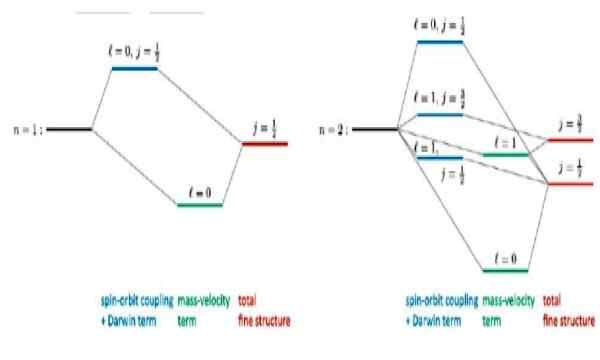Figur 4. Fin struktur som utspiller seg for basetilstand n = 1 og den første eksiterte tilstanden n = 2 i hydrogenatom. Kilde: R Wirnata. Relativistiske korreksjoner til hydrogenlignende atomer. ResearchGate.nett

Artikler av interesse

Broglie Atomic Model.

Chadwick Atomic Model.

Heisenberg Atomic Model.

Perrin Atomic Model.

Thomson Atomic Model.

Dalton Atomic Model.

Schrödinger atommodell.

Democritus Atomic Model.

Leucipo atommodell.

Bohr atommodell.

Gjeldende atommodell.

Referanser

1. Atomisk teori. Gjenopprettet fra Wikipedia.org.
2. Elektron magnetisk øyeblikk. Gjenopprettet fra Wikipedia.org.
3. Quanta: En håndbok med konsepter. (1974). Oxford University Press. Gjenopprettet fra Wikipedia.org.
4. Dirac Jordan Atomic Model. Gjenopprettet fra Prezi.com.
5. Det nye kvanteuniverset. Cambridge University Press. Gjenopprettet fra Wikipedia.org.