Torsjonsmoment

Vi forklarer hva som er tid for torsjon, dens egenskaper, formler, enheter, applikasjoner og plasseringsøvelser for å løse

Hva er tiden for torsjon?

Han Torsjonsmoment, dreiemoment eller kraftmoment er en styrke til å forårsake en sving. Etymologisk kalles det dreiemoment som en avledning av det engelske ordet Dreiemoment, fra latin Torque (vri).

Tidens tid (med hensyn til et bestemt punkt) er den fysiske størrelsen som følger av å utføre vektorproduktet mellom posisjonsvektorene til punktet der kraften brukes og den for kraften som utøves (i den angitte rekkefølgen). Dette øyeblikket avhenger av tre hovedelementer.

Den første av disse elementene er størrelsen på den påførte kraften, den andre er avstanden mellom punktet der den gjelder og punktet med hensyn til kroppen roterer (også kalt spakarmen), og det tredje elementet er vinkelpåføringen av sa styrke.

Større kraft, større sving er forårsaket. Det samme gjelder spakarmen: jo større avstand mellom punktet hvor kraften og punktet blir brukt med hensyn til den som produseres av svingen, jo større blir dette.

Logisk sett er tid for torsjon av spesiell interesse for bygging og industri, så vel som til stede i utallige hjemmeapplikasjoner, for eksempel når en nøtt blir presset med en engelsk nøkkel.

Formler

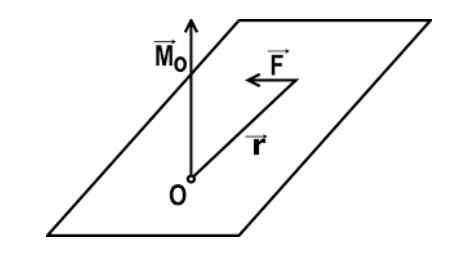
Det matematiske uttrykket av øyeblikk av torsjon av en styrke med hensyn til et punkt eller er gitt av: M = r x f

I dette uttrykket er r vektoren som forener punktet med O med punktet P for påføringen av kraften, og F er vektoren til den påførte kraften.

Kan tjene deg: elektrodynamikk

Momentenhetene for øyeblikket er n ∙ m, som selv om dimensjonalt tilsvarer juli (j), har en annen betydning og ikke bør forveksles.

Derfor tar momentmomentmodulen verdien gitt av følgende uttrykk:

M = r ∙ f ∙ sen α

I dette uttrykket er α vinkelen mellom styrkevektoren og vektoren R eller spakarmen. Tidens tid anses som positiv hvis kroppen dreier seg i motsatt retning av klokken nåler; Tvert imot, det er negativt når det svinger i en timeplan.

Enheter

Målingsenheten på torsjonen er produktet fra en kraftenhet med en enhet av avstand. Spesielt, i det internasjonale systemet med enheter, brukes Newton Metro hvis symbol er n • m.

På det dimensjonale nivået kan Newton Metro virke som tilsvarer juli; Imidlertid bør det ikke brukes juli for å uttrykke øyeblikk. Juli er en enhet for å måle verk eller energier som fra et konseptuelt synspunkt er veldig forskjellige fra torsjonsøyeblikk.

Tilsvarende presenterer torsjonsøyeblikket et vektorkarakter, som både er arbeids- og skalaenergi.

Torsjonsmomentegenskaper

Fra det sett følger det at øyeblikk av torsjon av en styrke med hensyn til et punkt representerer kapasiteten til en styrke eller et sett med styrker for å endre rotasjonen av nevnte legeme rundt en akse som passerer gjennom punktet.

Derfor genererer torsjonsøyeblikket en vinkelakselerasjon på kroppen og er en styrke på et vektorkarakter (så det er definert fra en modul, en retning og en følelse) som er til stede i mekanismene som har blitt utsatt for torsjon eller fleksjon.

Det kan tjene deg: Vy Canis Majoris: oppdagelse, egenskaper, struktur, trening og evolusjon

Torsjonstidspunktet vil være ugyldig hvis styrkevektoren og vektoren R har samme retning, siden verdien av sen α i så fall vil være ugyldig.

Resulterende dreiemoment

Gitt et visst organ som en seriekrefter virker, hvis de anvendte kreftene virker i samme plan, er torsjonsøyeblikket som følger av anvendelse av alle disse kreftene; Det er summen av torsjonsøyeblikkene som en konsekvens av hver styrke. Derfor er det oppfylt at:

M_T = ∑ m = m₁ + M_{2 +} M₃ +..

Det er selvfølgelig nødvendig å ta hensyn til kriteriet for tegn for torsjonsøyeblikk, som forklart ovenfor.

applikasjoner

Momentet er til stede i applikasjoner som hver dag som å presse en nøtt med en engelsk nøkkel, eller åpne eller lukke en kran eller en dør.

Imidlertid går applikasjonene dine mye lenger; Torsjonstidspunktet finnes også i aksjene på maskineriet eller i resultatet av innsatsen som bjelkene blir utsatt for. Derfor er applikasjonene innen industri og mekanikk mange og varierte.

Løste øvelser

Nedenfor er et par øvelser for å lette forståelsen av de ovennevnte forklarte.

Oppgave 1

Gitt følgende figur der avstandene mellom punkt O og punkt A og B er henholdsvis 10 cm og 20 cm:

a) Beregn verdien av momentmodulen med hensyn til punktet eller hvis en kraft på 20 n blir brukt på punkt a.

b) Beregn hva som skal være verdien av kraften som ble brukt i B for å oppnå samme torsjonstid som ble oppnådd i forrige seksjon.

Kan tjene deg: kontinuitetsligning

Løsning

For det første bør data til internasjonale systemenheter passere.

r_TIL = 0,1 m

r_B = 0,2 m

a) For å beregne torsjonsmomentet bruker vi følgende formel:

M = r ∙ f ∙ sen α = 0,1 ∙ 20 ∙ 1 = 2 n ∙ m

b) For å bestemme den forespurte kraften, fortsett på lignende måte:

M = r ∙ f ∙ sen α = 0,2 ∙ f ∙ 1 = 2 n ∙ m

Rydding f Det oppnås at:

F = 10 n

Oppgave 2

En kvinne utfører en styrke på 20 N på enden av en engelsk nøkkel 30 cm i lengde. Hvis vinkelen på kraften med nøkkelen til nøkkelen er 30 °, hva er tiden for vri i mutteren?

Løsning

Følgende formel brukes og opererer:

M = r ∙ f ∙ sen α = 0,3 ∙ 20 ∙ 0,5 = 3 n ∙ m