Gauss-Seidel Method Forklaring, applikasjoner, eksempler

Han Gauss-Seidel-metoden Det er en iterativ prosedyre å finne omtrentlige løsninger på et system med lineære algebraiske ligninger med vilkårlig valgt presisjon. Metoden gjelder firkantede matriser med ikke -null -elementer i diagonalene og konvergensen er garantert hvis matrisen er diagonalt dominerende.

Det ble opprettet av Carl Friedrich Gauss (1777-1855), som gjorde en privat demonstrasjon til en av studentene hans i 1823. Deretter ble den formelt utgitt av Philipp Ludwig von Seidel (1821-1896) i 1874, derav navnet på begge matematikere.

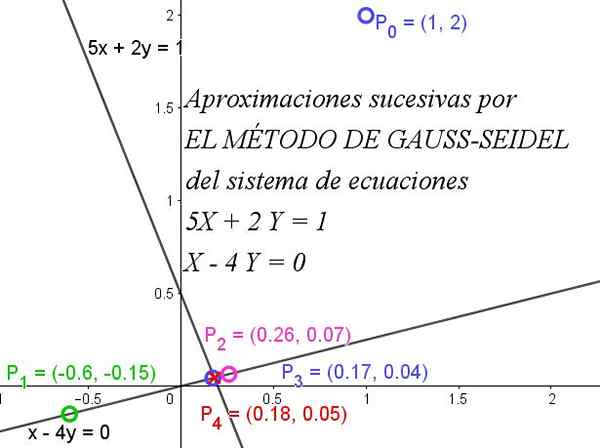
Figur 1. Gauss-Seidels metode konvergerer raskt for å få et ligningssystem. Kilde: f. Zapata.

For en full forståelse av metoden er det nødvendig å vite at en matrise er diagonalt dominerende når den absolutte verdien av det diagonale elementet i hver rad er større enn eller lik summen av de absolutte verdiene til de andre elementene av den samme raden.

Matematisk uttrykkes det som følger:

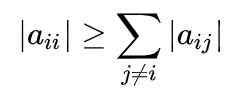
[TOC]

Forklaring gjennom en enkel sak

For å illustrere hva Gauss-Seidel-metoden vil ta et enkelt tilfelle, der du kan finne verdiene til X og Y i 2 × 2 lineære ligningssystem vist nedenfor:

5x + 2y = 1

X - 4y = 0

Trinn å følge

1- Først av alt må du avgjøre om konvergensen er trygg. Det blir umiddelbart observert at det i virkeligheten er et diagonalt dominerende system, siden den første raden i første rad har en større absolutt verdi enn de andre i første rad:

| 5 |> | 2 |

På samme måte er den andre koeffisienten for den andre raden også diagonalt dominerende:

| -4 |> | 1 |

2- Variablene X og Y er klare: 

X = (1 - 2y)/5

Y = x/4

3- En innledende vilkårlig verdi er plassert, kalt “frø”: xo = 1, ME = 2.

4

Det kan tjene deg: estimering etter intervaller

X1 = (1 - 2 meg)/5 = (1 - 2 × 2)/5 = -3/5 

Y1 = x1 / 4 = (-3/5) / 4 = -3/20 

5- Fortsett på en lignende måte for å oppnå den andre tilnærmingen av løsningen av ligningssystemet:

X2 = (1 - 2 y1)/5 = (1 - 2x (-3/20))/5 = 13/50 

Y2 = x2/4 = (13/50)/4 = 13/200

6- Tredje iterasjon:

X3 = (1 - 2 y2)/5 = (1 - 2 (13/200))/5 = 87/500

Y3 = x3/4 = (87/500)/4 = 87/2000

7- Fjerde iterasjon, som den endelige iterasjonen av denne illustrerende saken:

X4 = (1 - 2 y3)/5 = (1 - 2 (87/2000))/5 = 913/5000

Y4 = x4/4 = (913/5000)/4 = 913/20000

Disse verdiene sammenfaller ganske godt med løsningen som er funnet gjennom andre oppløsningsmetoder. Leseren kan sjekke det raskt ved hjelp av et online matematisk program.

Metodeanalyse

Som det fremgår av Gauss-Seidel-metoden, må de omtrentlige verdiene oppnådd for den forrige variabelen i det samme trinnet erstattes i følgende variabel. Dette skiller det fra andre iterative metoder som Jacobi, der hvert trinn krever tilnærminger til forrige trinn. 

Gauss-Seidels metode er ikke en parallell prosedyre, mens Gauss-Jordan er. Det er også grunnen til at Gauss-Seidel-metoden har en raskere konvergensfrie trinn-enn Jordans metode.

Når det gjelder den diagonalt dominerende matrikstilstanden, er dette ikke alltid fornøyd. I de fleste tilfeller er det imidlertid nok å utveksle rekkene til det opprinnelige systemet for å oppfylle tilstanden. I tillegg konvergerer metoden nesten alltid, selv når den diagonale dominanstilstanden ikke er oppfylt.

Det forrige resultatet, oppnådd med fire iterasjoner av Gauss-Seidel-metoden, kan skrives på en desimal måte:

Kan tjene deg: hvor mange symmetriaks?

X4 = 0.1826

Y4 = 0,04565

Den nøyaktige løsningen på systemet med lignende som er hevet er:

X = 2/11 = 0.1818

Y = 1/22 = 0,04545.

Så bare med 4 iterasjoner oppnås et resultat med en tusenvis av presisjon (0,001).

Figur 1 illustrerer hvordan påfølgende iterasjoner raskt konvergerer til den nøyaktige løsningen.

applikasjoner

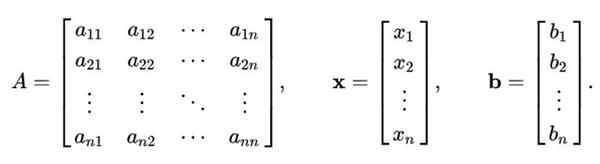
Gauss-Seidel-metoden er ikke bare begrenset til 2 × 2 lineære ligningssystem. Ovennevnte prosedyre kan generaliseres for å løse et lineært system av n ligninger med n Ukjente, som er representert matrise som dette:

TIL X = b

Hvor TIL Det er en matrise n x n, samtidig som X Det er vektor N -komponentene i variablene som skal beregnes; og b Det er en vektor som inneholder verdiene til uavhengige termer.

For å generalisere sekvensen av iterasjoner brukt i det illustrerende tilfellet til et N x N -system, som ønsker å beregne variabelen Xi, Følgende formel vil gjelde:

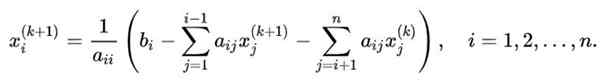
I denne ligningen:

- k Det er indeksen for verdien oppnådd i iterasjonen k.

-K+1 Indikerer den nye verdien i det følgende.

Det endelige antall iterasjoner bestemmes når verdien oppnådd i iterasjonen K+1 skiller seg fra de oppnådde rett før, i et beløp ε som er nettopp ønsket presisjon.

Eksempler på Gauss-Seidel-metoden

- Eksempel 1

Skriv en generell algoritme som lar deg beregne den omtrentlige løsningsvektoren X av et lineært system av NXN -ligninger, gitt koeffisientmatrisen TIL, Vektoren av uavhengige begreper b, Antall iterasjoner (iter) og den første eller "frø" av vektoren X.

Løsning

Algoritmen består av to "for" sykluser, den ene for antall iterasjoner og den andre for antall variabler. Det ville være som følger:

For k ∊ [1 ... iter]

For i ∊ [1… n]

X [i]: = (1/a [i, i])*(b [i] - ∑_{J = 1}ⁿ(A [i, j]*x [j]) + a [i, i]*x [i])

Kan tjene deg: desimalnotasjon

- Eksempel 2

Sjekk driften av den forrige algoritmen ved å søke på matematisk programvare Smath Studio Gratis og gratis, tilgjengelig for Windows og Android. Ta som et eksempel tilfellet med 2 × 2-matrisen som tjente oss til å illustrere Gauss-Seidel-metoden.

Løsning

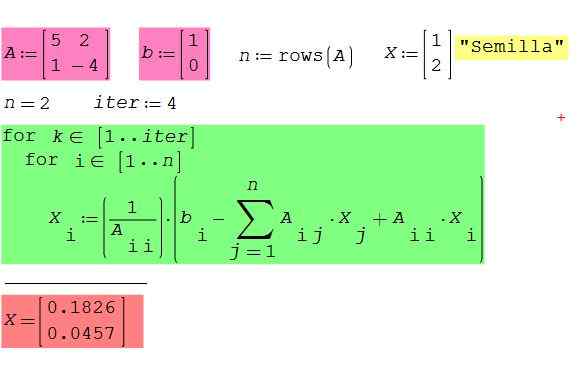Figur 2. System med ligninger av eksempel 2 x 2 ved hjelp av programvare Smath Studio. Kilde: f. Zapata.

- Eksempel 3

Bruk Gauss-Seidel-algoritmen for følgende 3 × 3-ligningssystem, som tidligere har blitt bestilt på en slik måte at de diagonale koeffisientene er dominerende (det vil si av større absolutt verdi enn de absolutte verdiene til koeffisientene til koeffisientene av samme rad):

9 x1 + 2 x2 - x3 = -2

7 x1 + 8 x2 + 5 x3 = 3

3 x1 + 4 x2 - 10 x3 = 6

Bruk nullvektoren som frø og vurder fem iterasjoner. Kommenter resultatet.

Løsning

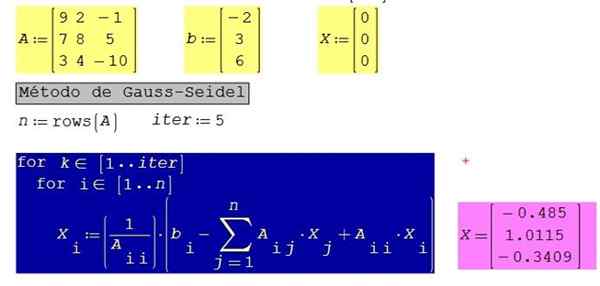Figur 3. Løsning av systemet med ligninger av det løste eksemplet 3, ved bruk av SMATH -studio. Kilde: f. Zapata.

For det samme systemet med 10 iterasjoner i stedet for 5 oppnås følgende resultater: x1 = -0.485; X2 = 1.0123; X3 = -0.3406

Dette indikerer at det er nok med fem iterasjoner for å oppnå tre presisjonsdesimaler og at metoden raskt formidler til løsningen.

- Eksempel 4

Ved hjelp av Gauss-Seidel-algoritmen som er gitt, finn løsningen av 4 × 4-ligningssystemet som skjer nedenfor:

10 x1 - x2 + 2 x3 + 0 x4 = 6

-1 x1 + 11 x2 - 1 x3 + 3 x4 = 25

2 x1 - 1 x2 + 10 x3 - 1 x4 = -11

0 x1 + 3 x2 - 1 x3 + 8 x4 = 15

For å starte metoden, bruk dette frøet:

x1 = 0, x2 = 0, x3 = 0 og x4 = 0

Tenk på 10 iterasjoner og estimere feilen i resultatet, sammenlignet med iterasjonsnummeret 11.

Løsning

Figur 4. Løsning av systemet med ligninger av det løste eksemplet 4, ved bruk av SMATH Studio. Kilde: f. Zapata.

Når du sammenligner med følgende iterasjon (nummer 11), er resultatet identisk. De største forskjellene mellom de to iterasjonene er i størrelsesorden 2 × 10^-8, Noe som betyr at løsningen som vises har en nøyaktighet på minst syv desimaler.

Referanser

1. Iterative løsningsmetoder. Gauss-Seidel. Gjenopprettet fra: Cimat.MX
2. Numeriske metoder. Gauss-Seidel. Gjenopprettet fra: Test.Cua.Uam.MX
3. Numerisk: Gauss-Seidel-metoden. Gjenopprettet fra: Lær i Linea.du.Edu.co
4. Wikipedia. Gauss-Seidel-metoden. Hentet fra: i. Wikipedia.com
5. Wikipedia. Gauss-Seidel-metoden. Gjenopprettet fra: er.Wikipedia.com