Multiplikasjon av brøk hvordan det gjøres, eksempler, øvelser

De Multiplikasjon av brøk Det er en aritmetisk operasjon mellom to eller flere brøk som gir opphav til en ny brøkdel. Telleren multipliserer tellerne for de deltakende brøkene, og nevneren er på samme måte.

La oss se det med et eksempel i følgende bilde. Anta at det er to brøk A/B og C/D, med B og D forskjellig fra 0.

Figur 1. Multiplikasjonen av brøk er en operasjon som gjøres online. Kilde: f. Zapata.

For å utføre multiplikasjonen mellom dem er produktet laget mellom telleren og også denominatoren. På denne måten opprettes en ny brøkdel der telleren og denominatoren er henholdsvis: (A × C) og (B × D).

Denne prosedyren utvides lett til multiplikasjonen av tre og flere brøkdeler. La oss se flere detaljer nedenfor.

Hvordan gjøres multiplikasjonen av brøkdeler?

Produktet kan symboliseres med et kors eller med et punkt ispedd brøkdeler. I tillegg må det tas i betraktning at brøkene kan ha et positivt tegn eller et negativt tegn, så det er nødvendig å være nøye med å følge tegnregelen:

-Når to antall like tegn multipliseres, er produktet positivt.

-Hvis to mengder forskjellige tegn multipliseres, er resultatet negativt.

Denne måten:

Når prosedyren er utført, blir brøkdelen forenklet, hvis mulig. Dette i tilfelle teller og nevner ikke er søskenbarn med hverandre. For eksempel:

Hvis teller og nevner av de deltakende brøkene ikke er søskenbarn med hverandre, er det praktisk å forenkle dem før du gjør multiplikasjonen av brøk. På denne måten oppnås mindre og mer håndterbare tall når du kjører produktene.

Kan tjene deg: hvor mange løsninger har en kvadratisk ligning?

Egenskaper for fraksjoner multiplikasjon

Produkt med 0

Enhver brøk multiplisert med 0 er lik 0:

Produkt av 1

Enhver brøk multiplisert med 1 er lik seg selv:

Derfor vurderes 1 Nøytralt element av multiplikasjon. Merk at hele nummer 1 har et brøkuttrykk:

På en slik måte at vi kan multiplisere til 1 med en hvilken som helst brøkdel, ved hjelp av regelen som allerede er forklart. Så:

Kommutativ eiendom

Multiplikasjonen av brøk er kommutativ, noe som betyr at rekkefølgen på faktorene ikke endrer produktet:

Assosiativ eiendom

Multiplikasjonen av brøk er også assosiativ, vi kan bekrefte ved å multiplisere tre brøk:

Hvor, som alltid, nevner B, D og F er forskjellige fra 0.

Med ord: Hvis vi skal multiplisere tre brøk, kan vi velge å lage produktet av de to første, og multiplisere resultatet med den tredje brøkdelen. Eller multipliser de to siste og resultatet til slutt multipliser det med den første av brøkene.

Uansett hvilken valgt ordre, vil resultatet være det samme. La oss sjekke det:

For å utføre operasjonen ble de to første brøkene multiplisert fra venstre til høyre. Resultatet ble multiplisert etter tur med den tredje brøkdelen for å oppnå det endelige resultatet.

Det andre alternativet er å multiplisere de to siste brøkene, og etterlate den første ventetiden. Leseren kan se at det mellomliggende resultatet består av to forskjellige fraksjoner fra de som er oppnådd på den andre måten. Men det endelige resultatet er det samme:

Distribuerende eiendommer angående summen

La tre fraksjoner A/B, C/D og E/F, med B, D og F forskjellig fra 0. Multiplikasjon er distribuerende med hensyn til sum.

Anta at vi vil utføre følgende operasjon:

Måten å gjennomføre den, gjennom denne eiendommen, er som følger:

Det kan tjene deg: Tukey Test: Det som er i tilfelle av eksempel løst trening

Derfor kan produktet av et tall for summen av to andre gjøres ved å legge til to produkter: det første for den andre og den første av den tredje. Det er veldig enkelt av et eksempel:

Det endelige resultatet virker forenklet maksimalt, som forklart ovenfor.

Eksempler

Multiplikasjon av en brøkdel av et heltall

Anta at du vil multiplisere en A/B -brøk med et heltall N:

Vi har tidligere sett at nummer 1 kan uttrykkes som en brøkdel, og bare plassere som nevner ved 1. Vi kan gjøre det samme med ethvert heltall n, siden det å dele det med 1 ikke endrer det i det hele tatt. Så:

For eksempel:

Eksempel 2: Multiplikasjon av en brøkdel med et blandet tall

Et blandet antall eller blandet brøkdel, er et som har en hel del og en brøkdel. For å utføre produktet fra et slikt tall, enten med en brøkdel, et annet blandet tall eller med et heltall, er det nødvendig å forvandle det i tur til brøkdel.

Brøkdelen som representerer et blandet tall er en Uekte brøk, a hvis teller har større absolutt verdi enn nevneren.

Vi kan få det gjennom summen av hele delen, praktisk uttrykt som en brøkdel ved å plassere en 1 som nevner, pluss den brøkdelte delen.

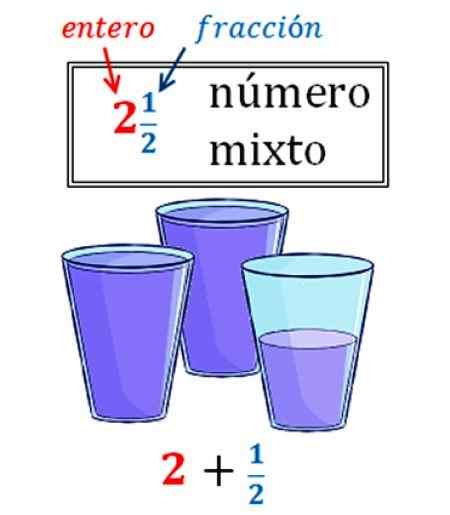Figur 2. Et blandet tall transformert til brøkdel. Kilde: Wikimedia Commons.

På bildet er det et eksempel på blandet tall, som viser hvor hyppig. Vi har 2 og et halvt glass vann, som som et blandet tall uttrykkes slik:

2 ½

Vi får den upassende brøkdelen som representerer den:

Anta nå at vi ønsker å finne de 3/4 delene av to og et halvt glass vann. Det vi må gjøre er å multiplisere 3/4 med den feilaktige brøkdelen:

Det kan tjene deg: Poisson Distribusjon: Formler, ligninger, modell, egenskaper

Løste øvelser

Oppgave 1

Gjennomfør følgende operasjon:

Løsning

Tallet 1 ¾ er et blandet tall. Hele delen er 1 og dens brøkdel er ¾. Hvis vi utfører operasjonen: 1 + ¾, blir det blandede tallet transformert til en feil brøkdel.

1 + ¾ = (4 + 3) /4 = 7/4

Når det blandede tallet fra feil brøk er transformert, utføres multiplikasjonsoperasjonen som vanlig:

Oppgave 2

Josés alder er ½ av 2/3 av Manuels alder. Hvis Manuel er 24 år gammel, hva er Josés alder?

Løsning

La X Age of José, en ukjent som vi må finne. Uttalelsen forteller oss at Manuels alder er 24 år, derfor er denne verdien kjent.

For å bestemme Josés alder, utfører vi operasjonene som er angitt med uttalelsen: "Josés alder er ½ av 2/3 av Manuel -alderen".

Dette er multiplikasjonen av to brøk for et heltall:

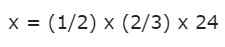
Vi kan multiplisere de to første brøkene i henhold til reglene beskrevet før. For sin del er tallet 24 et heltall, men vi vet allerede at det ikke er noe problem i å transformere det til en brøkdel, ganske enkelt ved å plassere en 1 som nevner:

Vi kan forenkle operasjonen i stor grad, og observerer at de 2 i telleren til den andre brøkdelen umiddelbart blir kansellert med de 2 som er som nevner i den første.

Dette er hva vi har igjen etter kansellering:

Derfor er José 8 år gammel.

Referanser

1. Baldor, a. 1986. Aritmetikk. Codex -utgaver og distribusjoner.
2. Carena, m. 2019. Matematikkhåndbok. National University of the Coast.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Sangaku Maths. Multiplikasjon av brøk. Gjenopprettet fra: sangakoo.com.
5. Smartick. Multiplikasjon av brøk. Gjenopprettet fra: Smartick.er.