Registrert vinkel på en sirkeldefinisjon, teoremer, eksempler

Han Registrert vinkel på en sirkel Det er den som har sin toppunkt på omkretsen og dens halvtett er tørr eller tangent til det samme. Som en konsekvens vil den registrerte vinkelen alltid være konveks eller flat.

I figur 1 er flere vinkler registrert i deres respektive omkretser representert. Vinkelen ∠EDF er registrert ved å ha sin toppunkt D på omkretsen og dens to semi -recrengers [av) og [df) tørking av omkretsen. 

Figur 1. Flere påskrevne vinkler om deres respektive omkretser. Kilde: f. Zapata med Geogebra.

Tilsvarende er vinkelen ∠HGI registrert, for å ha sin toppunkt i omkretsen og dens tørre sider til det samme.

Vinklene ∠KJR og ∠UST er også registrert med omkretsen. Den første har den ene Secant -siden og den andre tangenten, mens den andre har sine to sider tangent til omkretsen, og danner en flat planvinkel (180º).

Noen forfattere kaller en halvinskrevet vinkel til den som har en av sidene hans tangent til omkretsen, men i denne artikkelen regnes han som registrert.

Enhver registrert vinkel definerer eller sender en bue assosiert med det samme. For eksempel i figur 2 undergir den registrerte vinkelen ∠ABC buen A⌒C av lengde D.

Den samme figuren viser vinkelen ∠DOE, som ikke er registrert i omkretsen for ikke å ha sin toppunkt på omkretsen, men i sentrum eller.

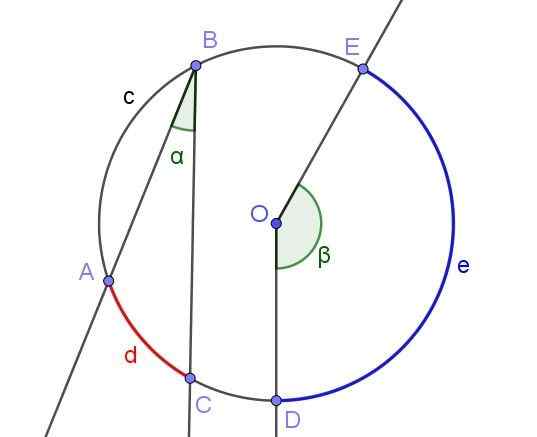Figur 2. Registrert vinkel ∠ABC og sentral vinkel ∠DOE. Kilde: f. Zapata med Geogebra.

[TOC]

Sentral vinkel

I tillegg til den registrerte vinkelen, Sentral vinkel, som er den hvis toppunkt er i midten av omkretsen og hvis sider kutter til omkretsen.

Kan tjene deg: Forskjell mellom en felles brøkdel og et desimaltall

Radianene mål på en sentral vinkel er kvotienten mellom buen som undergir, det vil si omkretsbuen mellom sidene av vinkelen og omkretsens radius.

Hvis omkretsen er enhetlig (radius 1), er lengden på buen i de samme radioenhetene målet på vinkelen i radianer.

Og når målet på vinkelen er nødvendig i grader, multipliseres tiltaket i radianer etter faktor 180º/π.

Vinklene måleinstrumenter bruker alltid en sentral vinkel, og lengden på buen underlagt av dette direkte kalibrert i grader. Dette betyr at når en vinkel måles, er i bakgrunnen det som måles lengden på buen underlagt av den sentrale vinkelen.

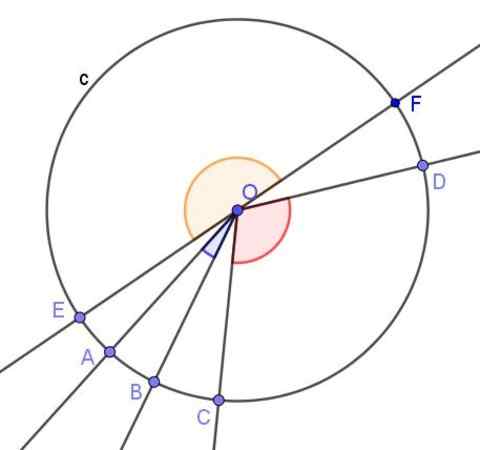Figur 3. Flere sentrale vinkler i omkretsen. Kilde: f. Zapata med Geogebra.

Teoremer

- Teorem 1 (registrert vinkel og sentral vinkel)

Målet på en registrert vinkel er halvparten av målet på den sentrale vinkelen, hvis begge vinklene subtite den samme buen.

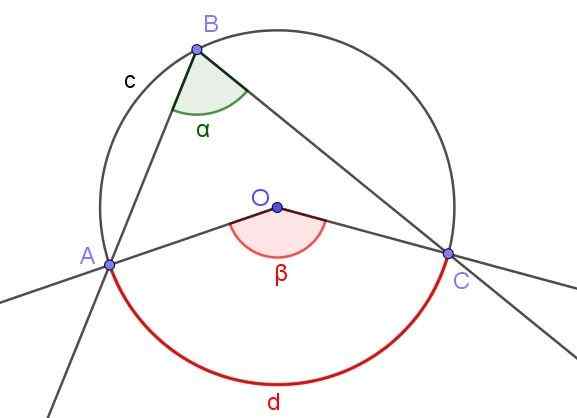Figur 4. Registrert vinkel ∠ABC og Central Angle ∠AOC som subtitter den samme buen A⌒C. Kilde: f. Zapata med Geogebra.

Figur 4 viser to vinkler ∠ABC og ∠AOC, som krysser den samme omkretsen A⌒C.

Hvis målet på den registrerte vinkelen er α, er β -målet på den sentrale vinkelen dobbelt sånt målet på den registrerte vinkelen (β = 2 α) fordi begge trekker den samme målte bue d.

Demonstrasjon 1

For å demonstrere teorem 1, vil flere spesielle tilfeller begynne, inntil det når den generelle saken.

Kan tjene deg: Sandwich Law: Forklaring og øvelser

Anta at en registrert vinkel, der en av sidene går gjennom sentrum av omkretsen, som vist i figur 5.

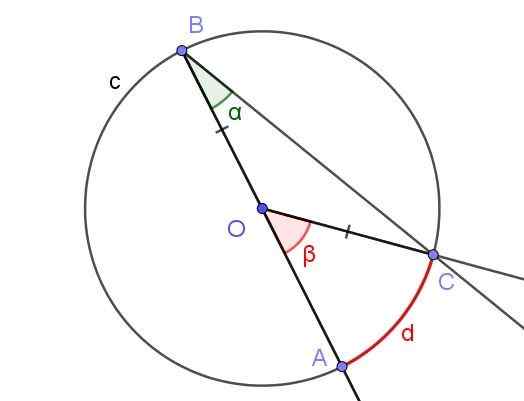Figur 5. Registrert vinkel ∠ABC med siden [BA) gjennom O og Central Angle ∠AOC. Kilde: f. Zapata med Geogebra.

I dette tilfellet dannes Cob Isosceles -trianten, siden [OC] = [OB].

I en isosceles -trekant er vinklene ved siden av basen de samme, derfor må de ∠BCO = ∠ABC = α. På den annen side ∠COB = 180º - β.

Tatt i betraktning summen av de interne vinklene til COB -trekanten du har:

α + α + (180º - β) = 180º

Der det følger at 2 α = β, eller hva som er ekvivalent: α = β/2. Dette sammenfaller med hva teorem 1 sier: Målet på den registrerte vinkelen er halvparten av den sentrale vinkelen, hvis begge vinklene sender inn det samme tauet [AC].

Demonstrasjon 1B

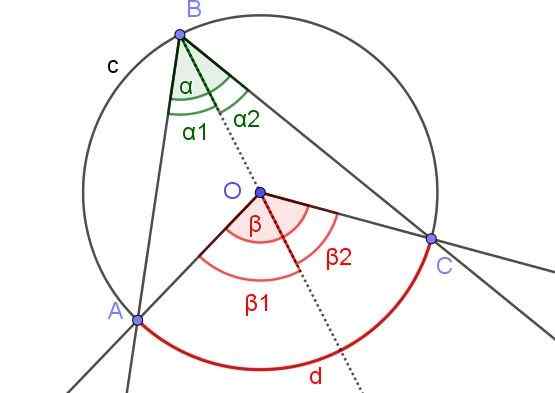Figur 6. Hjelpekonstruksjon for å demonstrere at α = β/2. Kilde: f. Zapata med Geogebra.

I dette tilfellet er det en innskrevet vinkel ∠ABC, der sentrum eller omkretsen er inne i vinkelen.

For å demonstrere teorem 1 i dette tilfellet, trekkes det semi -rettige hjelpe [BO), slik at det er to registrerte vinkler ∠ABO og ∠OBC ved siden av nevnte semi -recreational.

Tilsvarende har de de sentrale vinklene β₁ og β₂ ved siden av nevnte semi -recreational. På denne måten har du den samme situasjonen som i demonstrasjon 1, så det kan sies at α₂ = β₂ /2 og α₁ = β₁ /2. Som α = α₁ + α₂ og β = β₁ + β₂ Det er derfor at α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Kan tjene deg: typer integraler

Avslutningsvis α = β / 2, som oppfyller teorem 1.

- Teorem 2

Hvis to eller flere registrerte vinkler subtsen den samme buen, har de samme tiltak.

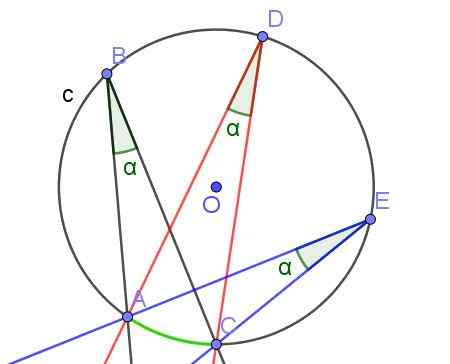Figur 7. Registrerte vinkler med like mål α, fordi de subtsen den samme buen A⌒C. Kilde: f. Zapata med Geogebra.

- Teorem 3

De registrerte vinklene underteksten Det er strenger med samme mål er de samme.

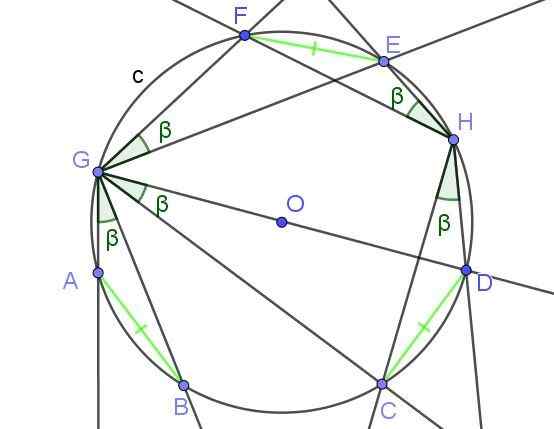Figur 8. De innskrevne vinklene som subtuse tau med like mål, har like mål β. Kilde: f. Zapata med Geogebra.

Eksempler

- Eksempel 1

Demonstrere at den innskrevne vinkelen subtites diameteren er en rett vinkel.

Løsning

Den sentrale vinkelen ∠AOB assosiert med diameter er en flat vinkel, hvis mål er 180º.

I henhold til teorem 1 har enhver vinkel registrert i omkretsen som sender det samme tauet (i dette tilfellet diameteren), som mål om halvparten av den sentrale vinkelen som subtitter det samme tauet, som for vårt eksempel er 180º/2 = 90º.

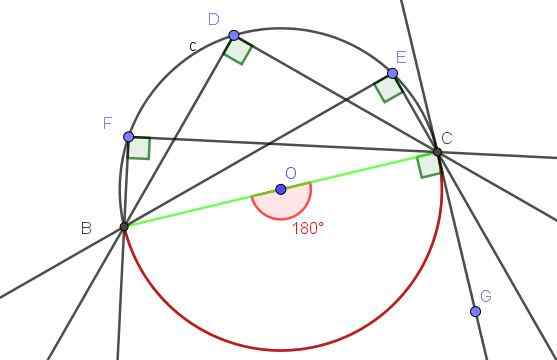Figur 9. Enhver registrert vinkel som underkaster seg diameter er en rett vinkel. Kilde: f. Zapata med Geogebra.

- Eksempel 2

Linjen (BC) tangenten i A A til omkrets C, bestemmer den innskrevne vinkelen ∠BAC (se figur 10).

Kontroller at teorem 1 i de registrerte vinklene er oppfylt.

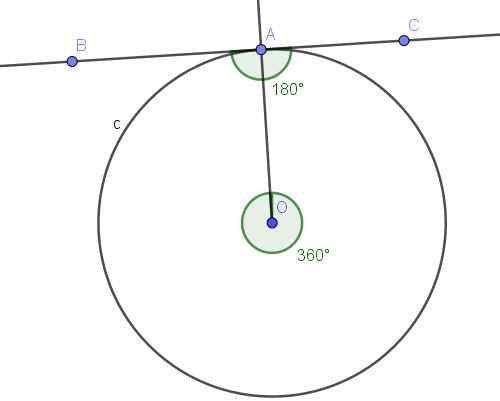Figur 10. Registrert vinkel BAC og dens konvekse sentrale vinkel AOA. Kilde: f. Zapata med Geogebra.

Løsning

Vinkelen ∠BAC er registrert fordi toppunktet er på omkretsen, og den.

På den annen side sender den innskrevne vinkelen ∠BAC A⌒A -buen, som er den komplette omkretsen. Den sentrale vinkelen som underlegger A⌒a -buen er en konveks vinkel hvis mål er full vinkel (360º).

Den registrerte vinkelen subtitter hele lysbuen måler halvparten av den tilhørende sentrale vinkelen, det vil si ∠BAC = 360º/2 = 180º.

Med alt det ovennevnte er det bevist at denne spesielle saken møter teorem 1.

Referanser

1. Baldor. (1973). Geometri og trigonometri. Sentralamerikansk kulturell redaksjon.
2. OG. TIL. (2003). Geometrielementer: med øvelser og kompassgeometri. University of Medellin.
3. Geometri 1st. Vinkler i omkretsen. Gjenopprettet fra: Edu.Xunta.er/
4. All vitenskap. Foreslåtte øvelser av vinkler i omkretsen. Gjenopprettet fra: Francesphysics.Blogspot.com
5. Wikipedia. Registrert vinkel. Gjenopprettet fra: er.Wikipedia.com