Nullvinkeldefinisjon og egenskaper, eksempler, øvelser

Han Nullvinkel Det er den hvis tiltak er verdt 0, både i grader og i radianer eller andre vinkler målesystem. Derfor mangler det amplitude eller åpning, for eksempel den mellom to parallelle linjer.

Selv om definisjonen høres ganske enkel ut, er nullvinkelen veldig nyttig i mange fysikk- og ingeniørapplikasjoner, så vel som i navigasjon og design.

Figur 1. Mellom hastigheten og akselerasjonen på bilen er det en nullvinkel, derfor går bilen raskere og raskere. Kilde: Wikimedia Commons.

Det er fysiske mengder som må justeres parallelt for å oppnå visse effekter: hvis en bil beveger seg rett på en motorvei og mellom hastighetsvektoren v og dens vektorakselerasjon til Det er 0º, bilen øker.

I den følgende figuren vises forskjellige typer vinkel inkludert nullvinkelen til høyre. Som det kan sees, mangler vinkel 0 amplitude eller åpning.

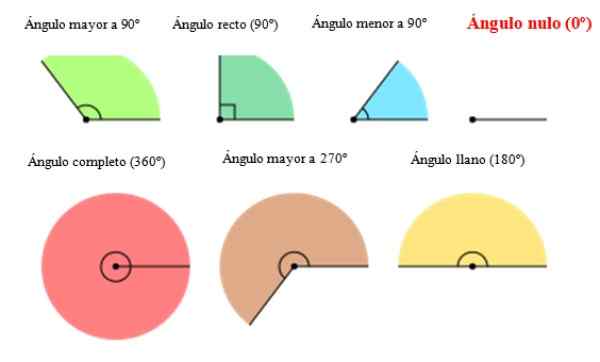Figur 2. Typer av vinkel, inkludert nullvinkelen. Kilde: Wikimedia Commons. ORIAS [CC BY-SA (https: // CreativeCommons.Org/lisenser/by-SA/3.0)].[TOC]

Eksempler på nullvinkler

Det er kjent at parallelle linjer danner en vinkel null. Når du har en horisontal linje, er dette parallelt med x -aksen til det kartesiske koordinatsystemet, derfor er dets tilbøyeligheter med hensyn til det 0. Med andre ord, horisontale linjer har en nullhelling.

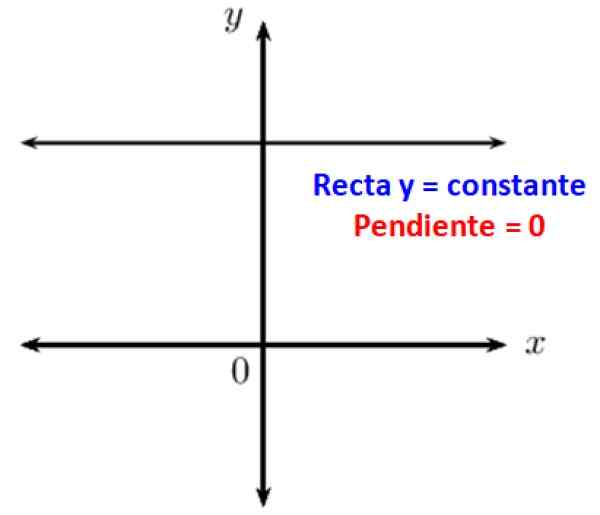Figur 3. Horisontale linjer har null i påvente av. Kilde: f. Zapata.

Også de trigonometriske årsakene til nullvinkelen er 0, 1 eller uendelig. Derfor er nullvinkelen til stede i mange fysiske situasjoner som involverer operasjoner med vektorer. Disse grunnene er:

Kan tjene deg: ordnet par

-Sen 0º = 0

-cos 0º = 1

-Tg 0º = 0

-sek 0º = 1

-Skade 0º → ∞

-Ctg 0º → ∞

Og de vil være nyttige for å analysere noen eksempler på situasjoner der tilstedeværelsen av nullvinkelen spiller en grunnleggende rolle:

- Effekter av nullvinkel på fysiske størrelser

Sum av vektorer

Når to vektorer er parallelle, er vinkelen mellom dem null, som sett i figur 4 ovenfor. I dette tilfellet blir summen av begge utført ved å plassere den ene etter den andre, og størrelsen på vektorsummen er summen av størrelsene på tilleggene (figur 4B).

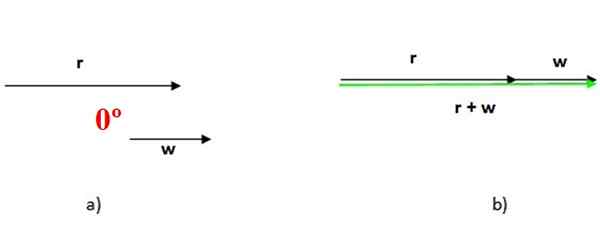Figur 4. Sum av parallelle vektorer, i dette tilfellet er vinkelen mellom dem en nullvinkel. Kilde: f. Zapata.

Når to vektorer er parallelle, er vinkelen mellom dem null, som sett i figur 4 ovenfor. I dette tilfellet blir summen av begge utført ved å plassere den ene etter den andre, og størrelsen på vektorsummen er summen av størrelsene på tilleggene (figur 4B)

Dreiemomentet eller dreiemomentet

Dreiemomentet eller dreiemomentet forårsaker rotasjon av en kropp. Det avhenger av størrelsen på den påførte kraften og hvordan den gjelder. Et veldig representativt eksempel er den engelske nøkkelen til figuren.

For å oppnå den beste svingseffekten, gjelder kraft vinkelrett på nøkkelhåndtaket, verken opp eller ned, men rotasjon er ikke forventet hvis kraften er parallell med håndtaket.

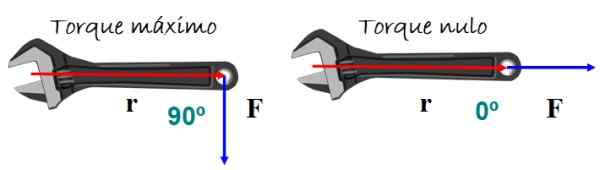Figur 5. Når vinkelen mellom posisjonen og styrkevektorene er ugyldig, oppstår ikke dreiemomentet, og det er derfor ingen svingseffekt. Kilde: f. Zapata.

Matematisk dreiemomentet τ Det er definert som vektor eller kryssprodukt mellom vektorene r (posisjonsvektor) og F (Kraftvektor) i figur 5:

Kan tjene deg: Statistikk filialer

τ = r x F

Størrelsen på dreiemomentet er:

τ = r f Sen θ

Å være θ vinkelen mellom r og F. Når sin θ = 0 er dreiemomentet ugyldig, i så fall θ = 0º (eller også 180º).

Elektrisk feltstrøm

Den elektriske feltstrømmen er en skalær størrelse som avhenger av intensiteten til det elektriske feltet, så vel som overflateorienteringen som den krysser.

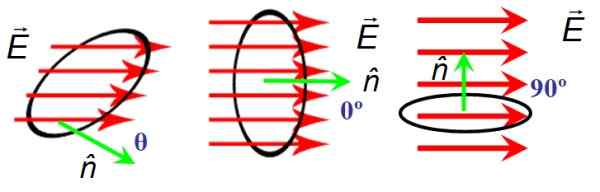
I figur 6 er det en sirkulær overflate av område A som de elektriske feltlinjene passerer OG. Overflateorienteringen er gitt av den normale vektoren n. Til venstre feltet og den normale vektoren danner en aktører vilkårlig vinkel θ, i sentrum danner de en nullvinkel og høyre er vinkelrett.

Når OG og n De er vinkelrett, feltlinjene krysser ikke overflaten og derfor er strømmen null, mens når vinkelen mellom OG og n Det er ugyldig, linjene krysser overflaten fullstendig.

Begynner den elektriske feltstrømmen med den greske bokstaven φ (lyder “fi”), dens definisjon for et enhetlig felt som i figuren, det forblir slik:

Φ = OG•nTIL

Punktet i midten av begge vektorer betegner punktet eller skalarproduktet, som vekselvis definerer:

Φ = OG•nA = eacosθ

Fet og piler over bokstaven er ressurser for å skille mellom en vektor og dens størrelse, som er betegnet med normale bokstaver. Siden cos 0 = 1, er strømmen maksimal når OG og n De er parallelle.

Figur 6. Den elektriske feltstrømmen avhenger av retningen mellom overflaten og det elektriske feltet. Kilde: f. Zapata.

Øvelser

- Oppgave 1

To styrker P og Q De virker samtidig på et rettidig objekt X, begge krefter danner i utgangspunktet en vinkel θ mellom dem. Hva som skjer med størrelsen på den resulterende kraften når θ avtar til den blir kansellert?

Kan tjene deg: evaluering av funksjoner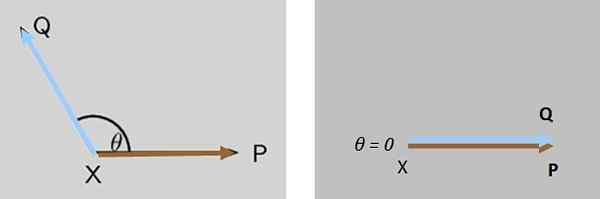 Figur 7. Vinkelen mellom to krefter som virker på et legeme avtar til størrelsen på den resulterende kraften skaffer seg sin maksimale verdi blir kansellert i dette tilfellet. Kilde: f. Zapata.

Løsning

Størrelsen på den resulterende kraften Q + P Den øker gradvis til den er maksimal når Q og P De er helt parallelle (figur 7 til høyre).

- Oppgave 2

Angi om nullvinkelen er en løsning av følgende trigonometriske ligning:

cos 2x = 1 + 4se x

Løsning

En trigonometrisk ligning er en der det ukjente er en del av argumentet om en trigonometrisk grunn. For å løse den foreslåtte ligningen, er det praktisk å benytte seg av formelen for dobbeltvinkelen kosinus:

cos 2x = cos² X - Sen² x

For på denne måten blir argumentet på venstre side x i stedet for 2x. Så:

Cos² X - Sen² x = 1 + 4sen x

På den annen side cos² X + sen² x = 1, så:

Cos² X - Sen² x = cos² X + sen² x + 4sen x

Begrepet cos² X blir kansellert og gjenstår:

- Sen² x = sen² x + 4sen x → - 2sen² x - 4Senx = 0 → 2sen² x + 4Senx = 0

Nå gjøres neste endring av variabelen: Senx = U og ligningen transformeres til:

2U² + 4U = 0

2U (u+4) = 0

Hvis løsninger er: u = 0 og u = -4. Å returnere endringen vi ville ha to muligheter: sin x = 0 og Senx = -4. Denne siste løsningen er ikke levedyktig, fordi brystet i noen vinkel er mellom -1 og 1, så vi sitter igjen med det første alternativet:

sin x = 0

Derfor er x = 0º en løsning, men serverer også enhver vinkel hvis sinus er 0, som også kan være 180º (π radianer), 360º (2 π radianer) og de respektive negativene også.

Den mest generelle løsningen av den trigonometriske ligningen er: x = kπ hvor k = 0, ± 1, ± 2, ± 3, .. . k et heltallnummer.

Referanser

1. Baldor, a. 2004. Flat- og romgeometri med trigonometri. Kulturpublikasjoner s.TIL. Av c.V. Mexico.
2. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 3. Partikkelsystemer. Redigert av Douglas Figueroa (USB).
3. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 5. Elektrisk interaksjon. Redigert av Douglas Figueroa (USB).
4. Onlinemathlearning. Typer vinkler. Hentet fra: Onlinemathlearning.com.
5. Zill, d. 2012. Algebra, trigonometri og analytisk geometri. McGraw Hill Inter -American.