Tau (geometri) lengde, teorem og øvelser

EN tau, I flat geometri er det linjesegmentet som går sammen med to punkter fra en kurve. Det sies at linjen som inneholder dette segmentet er en tørkelinje til kurven. Det er ofte en omkrets, men du kan absolutt trekke strenger inn i mange andre kurver, for eksempel ellipser og lignelser.

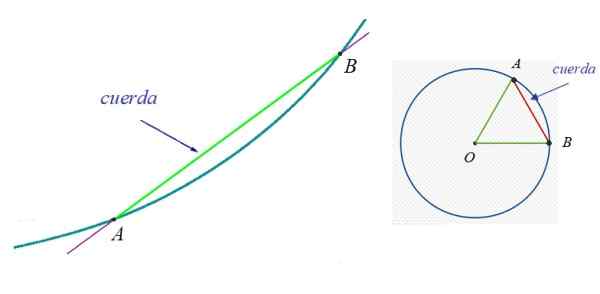
I figur 1 til venstre er det en kurve, som punktene A og B tilhører. Tauet mellom A og B er det grønne segmentet. Til høyre er en omkrets og en av strengene deres, siden det er mulig å spore uendelig.

Figur 1. Til venstre tauet til en vilkårlig kurve og til høyre tauet til en sirkel. Kilde: Wikimedia Commons.

I omkretsen er diameteren spesielt interessant, som også er kjent som Major tau. Det er et tau som alltid inneholder sentrum av omkretsen og måler det dobbelte av radius.

Følgende figur er representert med radius, diameter, et tau og også buen til en sirkel. Riktig identifisere hver og en er viktig når du løser problemer.

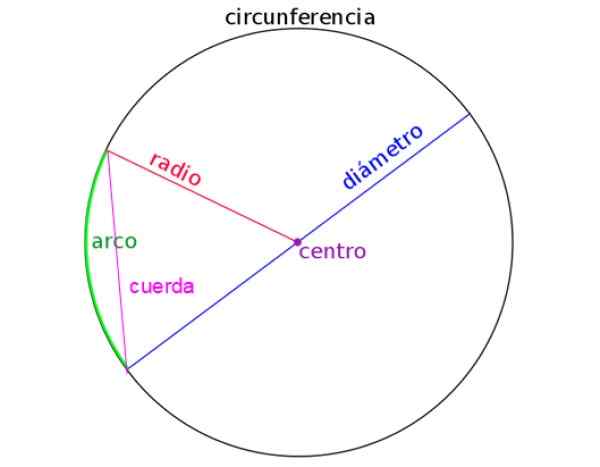Figur 2. Elementer i omkretsen. Kilde: Wikimedia Commons.

[TOC]

Tauets lengde på en omkrets

Vi kan beregne lengden på tauet i en sirkel fra figur 3A og 3B. Merk at en trekant alltid dannes med to like sider (isosceles): OA og OB -segmentene, som måler R, omkretsens radius. Den tredje siden av trekanten er segment AB, kalt C, som er nettopp lengden på tauet.

Det er nødvendig å trekke en linje vinkelrett på C -tauet for å halve i vinkelen θ som eksisterer mellom de to radioene og hvis toppunkt er sentrum eller omkretsen. Dette er en Sentral vinkel -Fordi toppunktet er midt- og bisektorinjen også er en sikring av omkretsen.

Det kan tjene deg: radikale egenskaper

Umiddelbart dannes to rektangler, hvis hypotenuse. Siden bisektoren, og med den, deler diameteren i to deler som er lik tauet, viser det seg at ett av bena er halvparten av C, som indikert i figur 3B.

Fra definisjonen av brystet i en vinkel:

sin (θ/2) = motsatt/hypotenusa kateto = (c/2)/r

Derfor:

sin (θ/2) = c/2r

C = 2r Sen (θ/2)

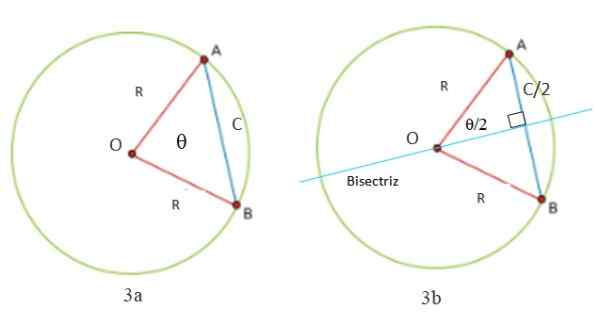Figur 3. Trekanten dannet av to radioer og et omkretstau er isosceles (figur 3), siden det har to sider like. Bisektoren deler den i to rektangler trekanter (figur 3B). Kilde: Utarbeidet av F. Zapata.

Strengsteorem 

Strengsteoremet sier:

Hvis noen to tau krysser hverandre på et tidspunkt, er produktet av lengden på segmentene som vises på en av strengene, lik produktet av lengden på segmentene som er definert i det andre tauet.

Følgende figur viser to strenger av samme omkrets: AB og CD, som krysser hverandre på punkt P. I AB -tauet er AP- og PB -segmentene definert, mens CP og PD er definert i CD -tauet. I følge teoremet:

Ap . PB = CP . S

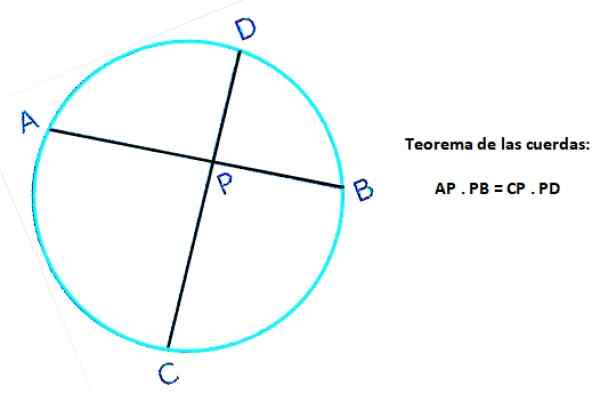Figur 4. Tauet til en omkrets. Kilde: f. Zapata.

Løste strengerøvelser

- Oppgave 1

En sirkel har et tau på 48 cm, som er 7 cm fra sentrum. Beregn sirkelområdet og omkretsen av omkretsen.

Løsning  

For å beregne sirkelen et område, er det nok å kjenne til omkretsens radius til torget, siden det er oppfylt:

A = π.R²

Nå er figuren som er dannet med dataene som er gitt, en rektangel -trekant, hvis ben er henholdsvis 7 og 24 cm.

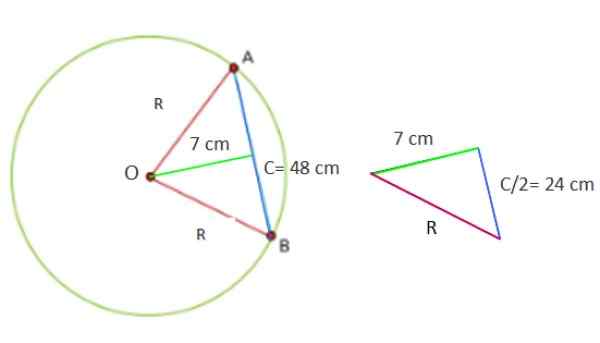Figur 5. Geometri for løst øvelse 1. Kilde: f. Zapata.

Derfor for å finne verdien av r² Pythagoras c teorem brukes direkte² = a² + b², Siden R er hypotenusen til trekanten:

Kan tjene deg: Nullvinkel: Definisjon og egenskaper, eksempler, øvelser

R² = (7 cm)² + (24 cm)² = 625 cm²

Da er det forespurte området:

A = π. 625 cm² = 1963.5 cm²

Når det gjelder omkretsen eller lengden på omkretsen, beregnes den av:

L = 2π. R

Erstatte verdier:

R = √625 cm² = 25 cm

L = 2π. 25 cm = 157.1 cm.

- Oppgave 2

Bestem lengden på tauet til en sirkel hvis ligning er:

x² + og² - 6x - 14y -111 = 0

Det er kjent at koordinatene til midtpunktet til tauet er P (17/2; 7/2).

Løsning

Midtpunktet til P -tauet tilhører ikke omkretsen, men tauets ekstreme punkter ja. Problemet kan løses ved hjelp av Strings Theorem tidligere oppgitt, men først er det praktisk.

Trinn 1: Få den kanoniske ligningen av omkretsen

Den kanoniske ligningen av omkretsen med sentrum (h, k) er:

(X-H)² + (Y-k)² = R²

For å få det, er det nødvendig å fullføre firkanter:

(x² - 6x) + (og² - 14y) -111 = 0

Merk at 6x = 2.(3x) og 14y = 2.(7y), slik at det forrige uttrykket blir skrevet om, og er uendret:

(x² - 6x+3²-3²) + (og² - 14y+7²-7²) -111 = 0

Og nå, husker definisjonen av bemerkelsesverdig produkt (A-B)² = a² - 2ab + b² Det kan skrives:

(X - 3)² - 3² + (og - 7)² - 7² - 111 = 0

= (x - 3)² + (og - 7)² = 111 + 3² + 7² → (x - 3)² + (og - 7)² = 169

Omkretsen har et senter (3,7) og radio r = √169 = 13. Følgende figur viser grafen over omkretsen og strengene som skal brukes i teoremet:

Kan tjene deg: Hva er de 7 elementene i omkretsen?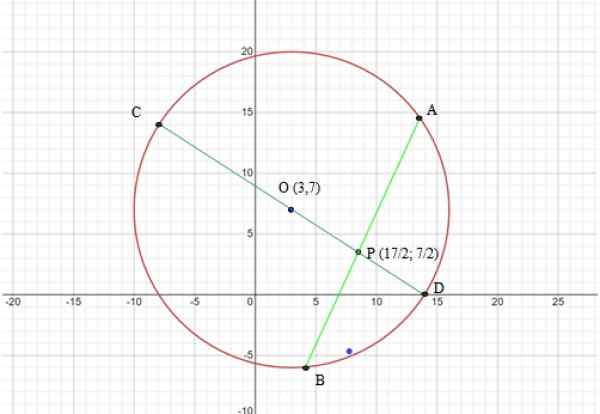Figur 6. Graf over omkretsen av øvelsen løst 2. Kilde: f. Zapata gjennom den elektroniske grafiske kalkulatoren Mathway.

Trinn 2: Bestem segmentene som skal brukes i strengsteoremet

Segmentene som skal brukes er CD- og AB -strengene, ifølge figur 6 er begge kuttet på punkt P, derfor:

CP . PD = AP. Pb

Nå skal vi finne avstanden mellom punktene O og P, siden dette vil gi oss lengden på OP -segmentet. Hvis vi legger radius til denne lengden, vil vi ha CP -segmentet.

Avstanden d_Op Mellom to koordinatpunkter (x₁,og₁) og (x₂,og₂) er:

d_Op² = Op² = (x₂ - x₁)² + (og₂ - og₁)² = (3- 17/2)² + (7-7/2)² = 121/4 + 49/4 = 170/4

d_Op = Op = √170 /2

Med alle oppnådde resultater, pluss grafen, bygger vi følgende liste over segmenter (se figur 6):

CO = 13 cm = r

Op = √170 /2 cm

Cp = op + r = 13 + √170 /2 cm

PD = OD - OP = 13 - √170 /2 cm

AP = Pb

2.AP = taulengde

Erstatter i strengsteoremet:

CP . PD = AP . PB = [(13 +√170 /2) . (13 -√170 /2)] = AP²

[169-170/4] = AP²

253/2 = ap²

AP = √ (253/2)

Lengden på tauet er 2.AP = 2 (√253/2) = √506

Kan leseren løse problemet på en annen måte?

Referanser

1. Baldor, a. 2004. Flat- og romgeometri med trigonometri. Kulturpublikasjoner s.TIL. Av c.V. Mexico.
2. C-K12. Lenght av et akkord. Gjenopprettet fra: CK12.org.
3. Escobar, J. Omkretsen. Gjenopprettet fra: Matematikk.du.Edu.co.
4. VILLENA, m. Konisk. Hentet fra: DSPACE.Espol.Edu.Ec.
5. Wikipedia. Tau (geometri). Gjenopprettet fra: er.Wikipedia.org.