Komplementære vinkler som og hvordan beregnes, eksempler, øvelser

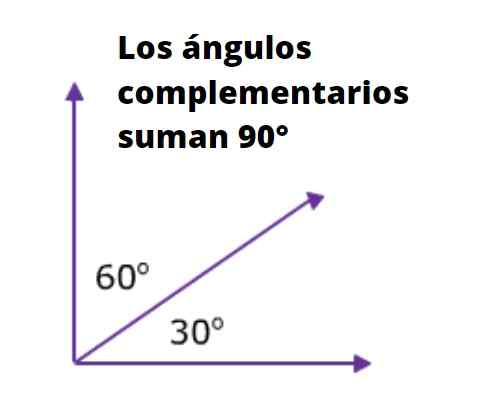
To eller flere vinkler er komplementære vinkler Hvis summen av tiltakene tilsvarer den i rett vinkel. Som kjent er målet på en rett vinkel i grader 90º, og i radianer er det π/2.

For eksempel er de to vinklene ved siden av hypotenusen til en rektangel -trekant komplementær til hverandre, siden summen av tiltakene deres er 90º. Følgende figur er veldig illustrerende om det:

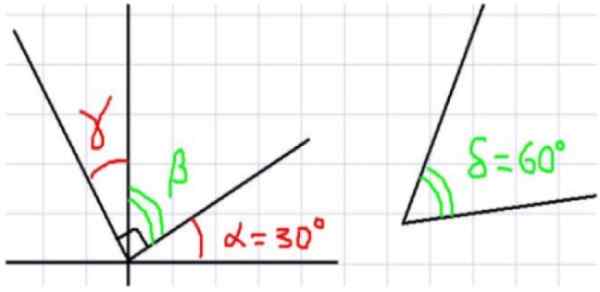Figur 1. Til venstre, flere vinkler med et felles toppunkt. Til høyre en vinkel på 60º som kompletterer vinkelen α (alfa). Kilde: f. Zapata.

Figur 1 viser totalt fire vinkler. α og β er komplementære siden de er ved siden av og dens fulle sum en rett vinkel. Tilsvarende β er komplementær til γ, der det følger at γ og α er av like store mål.

Nå som summen av α og Δ er lik 90 grader, kan det sies at α og Δ er komplementære. I tillegg, ettersom β og Δ har samme komplementære α, kan det sies at β og Δ har samme tiltak.

 [TOC]

Eksempler på komplementære vinkler

I de følgende eksempler blir det bedt om å finne de ukjente vinklene, angitt med avhør i figur 2.

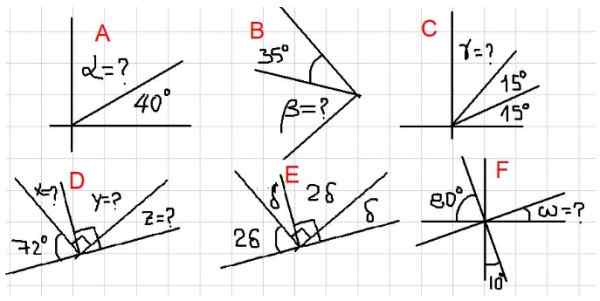Figur 2. Ulike eksempler på komplementære vinkler. Kilde: f. Zapata.

- Eksempler A, B og C

Følgende eksempler er i rekkefølge av kompleksitet.

Eksempel a

I den øvre figuren har vi at de tilstøtende vinklene α og 40º legger opp til en rett vinkel. Det er α + 40º = 90º, derfor α = 90º- 40º = 50º.

Eksempel b

Ettersom β er komplementær med vinkelen på 35º, deretter β = 90º - 35º = 55º.

Kan tjene deg: orthoedro: Formler, område, volum, diagonal, eksempler

Eksempel c

Fra figur 2C, summen av γ + 15º + 15º = 90º. Det vil si at γ er komplementær til vinkel 30 = 15º + 15º. Så det:

γ = 90º- 30º = 60º

- Eksempler D, E og F

I disse eksemplene er det flere vinkler involvert. For å finne de ukjente, må leseren bruke begrepet komplementær vinkel så mange ganger som nødvendig.

Eksempel d

Ettersom x er komplementær med 72º, følger det at x = 90º - 72º = 18º. I tillegg og det er komplementært med x, deretter y = 90º - 18º = 72º.

Endelig er z komplementær til og. Fra alt dette følger det at det:

Z = 90º - 72º = 18º

Eksempel e

Vinklene Δ og 2δ er komplementære, derfor Δ + 2Δ = 90º.

Det er 3δ = 90º, noe som innebærer at Δ = 90º / 3 = 30º.

Eksempel f

Hvis vi kaller vinkelen mellom ω og den på 10, må den suppleres til dem, fordi det observeres at deres komplette summen er en rett vinkel. Der det følger at u = 80º. Som u er komplementær med ω, deretter ω = 10º.

Øvelser

Tre øvelser er foreslått nedenfor. I dem alle må verdien av vinkler A og B finnes i grader, slik at forholdene vist i figur 3 er oppfylt.

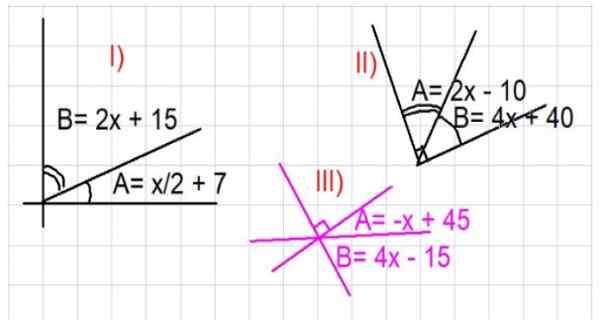Figur 3. Illustrasjoner for komplementære vinkler øvelser. Kilde: f. Zapata.

- Oppgave 1

Bestem verdiene til vinkler A og B i del I) i figur 3.

Løsning

Fra figuren som er vist, sees det at a og b er komplementære, derfor a + b = 90º. Uttrykket av A og B erstattes som en funksjon av x gitt i del I):

Kan tjene deg: konvergensradio: Definisjon, eksempler og øvelser løst

(x/2 + 7) + (2x + 15) = 90

Da er begrepene riktig gruppert og en enkel lineær ligning oppnås:

(5x/2) + 22 = 90

Trekker 22 i begge medlemmene er:

5x/2 = 90 -22 = 68

Og til slutt blir verdien av x fjernet:

x = 2*68/5 = 136/5

Nå er vinkelen funnet og erstatter verdien av x:

A = (136/5)/2 +7 = 103/5 = 20,6 º.

Mens vinkel B er:

B = 2*136/5 + 15 = 347/5º = 69,4º .

- Oppgave 2

Finn verdiene til vinkler A og B av bilde II, figur 3.

Løsning

Igjen, som A og B er komplementære vinkler, må du: a + b = 90º. Erstatte uttrykket av a og b som en funksjon av x gitt i del II) i figur 3 er:

(2x - 10) + (4x +40) = 90

De lignende begrepene er gruppert for å oppnå ligningen:

6 x + 30 = 90

Å dele begge medlemmene mellom 6 oppnås:

x + 5 = 15

Der det følger at x = 10º.

Derfor:

A = 2*10 - 10 = 10º

B = 4*10 + 40 = 80º.

- Øvelse 3

Bestem verdiene til vinkler A og B i del III) i figur 3.

Løsning

Figuren er nøye analysert for å se etter komplementære vinkler. I dette tilfellet må du + b = 90 grader. Ved å erstatte uttrykket av a og b som en funksjon av x gitt i figuren, har du:

(-X +45) + (4x -15) = 90

3 x + 30 = 90

Å dele begge medlemmene med 3 er følgende:

x + 10 = 30

Der det følger at x = 20º.

Det vil si at vinkelen a = -20 +45 = 25º. Og for sin del: B = 4*20 -15 = 65º.

Vinkelrett sider vinkler

Det sies at to vinkler er vinkelrett sider Hvis hver side har tilsvarende vinkelrett i den andre. Følgende figur tydeliggjør konseptet:

Kan tjene deg: sammensatt suksess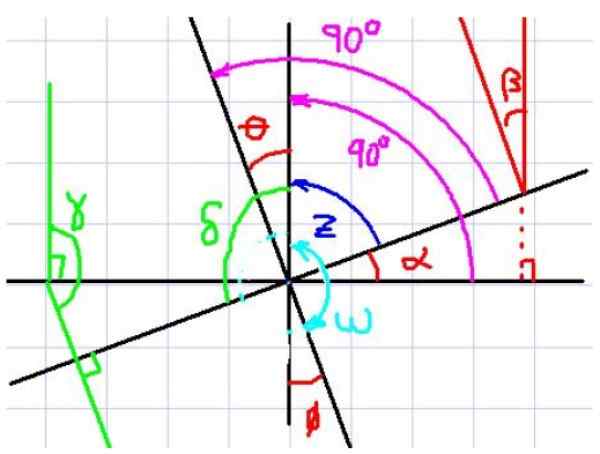Figur 4. Vinkelrett sider vinkler. Kilde: f. Zapata.

I figur 4 observeres vinklene α og θ for eksempel. Legg nå merke til at hver vinkel har tilsvarende vinkelrett i den andre vinkelen.

Det ser også at α og θ har samme utfyllende vinkel z, Derfor konkluderer observatøren umiddelbart at α og θ har samme tiltak. Det ser ut til at hvis to vinkler har vinkelrett sider med hverandre, er de de samme, men la oss se en annen sak.

Vurder nå vinklene α og ω. Disse to vinklene har også tilsvarende vinkelrett side, men det kan ikke sies at de har like mål, siden den ene er akutt og den andre er stump.

Merk at ω + θ = 180º. Foruten θ = α. Hvis du erstatter dette uttrykket av z i den første ligningen får du:

Δ + α = 180º, som Δ og α er vinkler på gjensidig vinkelrett sider.

Generell regel for vinkelrett sider vinkler 

Fra de nevnte, en regel som alltid er oppfylt at vinklene har vinkelrett sider kan etableres:

Hvis to vinkler er gjensidig vinkelrett sider, er de de samme hvis begge er akutte eller begge er stump. Ellers, hvis den ene er akutt og den andre er stump, er de supplerende, det vil si at de legger til 180º.

Bruke denne regelen og med henvisning til vinklene i figur 4 kan vi bekrefte følgende:

α = β = θ = φ

γ = Δ

Med den supplerende vinkelen til α, β, θ og φ.

Referanser

1. Baldor, J. TIL. 1973. Flat og romgeometri. Sentralamerikansk kulturell. 
2. Matematiske lover og formler. Vinkelmålingssystemer. Hentet fra: Ingemecanica.com.
3. Wentworth, g. Planetgeometri. Gjenopprettet fra: Gutenberg.org.
4. Wikipedia. Komplementære vinkler. Gjenopprettet fra: er.Wikipedia.com
5. Wikipedia. Transportør. Gjenopprettet fra: er.Wikipedia.com
6. Zapata f. Goniometer: historie, deler, drift. Hentet fra: Lifer.com