Sentralsymmetriegenskaper, eksempler og øvelser

To poeng A og 'har Sentral symmetri angående et punkt eller når AA -segmentet 'går gjennom det og er også midtpunktet til AA'. Til poenget eller kalles Symmetry Center.

Den sentrale symmetriske av en ABC -trekant med hensyn til ett punkt eller, er en annen trekant a'b'c 'som har følgende egenskaper:

-Homologe segmenter er like lengde 

-Deres tilsvarende vinkler har samme mål.

Figur 1. ABC Triangle og dens symmetriske a'b'c '. Kilde: f. Zapata.

I figur 1 en ABC -trekant (rød) og dens sentrale symmetriske a'b'c '(grønn), med hensyn til symmetri -sentrum eller. 

I samme figur ville en oppmerksom observatør innse at det samme resultatet oppnås ved å bruke en original trekantrotasjon, så lenge den er 180º og fokusert på eller.

Derfor tilsvarer en sentral symmetri en 180º sving med hensyn til symmetri -sentrum.

[TOC]

Egenskapene til sentral symmetri

En sentral symmetri har følgende egenskaper:

-Symmetry Center er midtpunktet i segmentet som blir med et punkt med sitt symmetriske.

-Et symmetrisk punkt for et annet som ligger i symmetri -senteret, sammenfaller med Symmetri sentrum.

-The Central Symmetric of a Triangle er en kongruent trekant (lik) til originalen.

-Bildet ved sentral symmetri av en omkrets er en annen omkrets av lik radius.

-En sirkel har sentral symmetri med hensyn til sitt eget senter.

Figur 2. Design med sentral symmetri. Kilde: Pixabay.

-Ellipsen har sentral symmetri med hensyn til sentrum.

-Et segment har sentral symmetri med hensyn til midtpunktet.

-Den likesidelige trekanten har ingen sentral symmetri med hensyn til sentrum, fordi dens symmetriske, selv om den er kongruent med den første, gir en likestående trekant dreid.

Det kan tjene deg: y = 3sen (4x) funksjonsperiode

-Firkanter har sentral symmetri med hensyn til sentrum.

-En Pentagon mangler sentralsymmetri med hensyn til sentrum.

-Vanlige polygoner har sentral symmetri når de har et antall dreiemomentsider.

Eksempler

Symmetri -kriteriene har mange applikasjoner innen vitenskap og ingeniørfag. Sentral symmetri er til stede i naturen, for eksempel iskrystaller og spindelvev har denne typen symmetri.

I tillegg løses mange problemer lett når eksistensen av sentral symmetri og andre typer symmetri brukes. Derfor er det praktisk å identifisere seg raskt når det oppstår.

Figur 3. Iskrystaller har sentral symmetri. Kilde: Pixabay.

Eksempel 1

Gitt et punkt P av koordinater (a, b), må du finne koordinatene til dets symmetriske p 'angående opprinnelse eller koordinater (0, 0).

Den første tingen er å bygge P 'P', som det trekkes en linje som går gjennom opprinnelsen eller og gjennom punkt P. Ligningen for denne linjen er y = (b/a) x.

La oss nå kalle (a ', b') koordinatene til det symmetriske punktet p '. Punkt p. I tillegg må OP -avstanden være lik OP ', som analytisk skriver som dette:

√ (a² + b²) = √ (a '² + B '² )

Følgende er å erstatte b '= [(b/a).A '] i forrige uttrykk og firkant på begge sider av likhet for å eliminere kvadratroten: (a² + b²) = [a '² + (b²/til²).til'²]

Ved å trekke ut vanlig faktor og forenkle, nås den til '² = a². Denne ligningen har to virkelige løsninger: a '= +a eller a' = -a. 

For å få b 'bruker vi igjen b' = (b/a) a '. Hvis den positive løsningen av A erstattes, er det nådd at B '= B. Og når den negative løsningen byttes ut, så b '= -B. 

Kan tjene deg: Hva er de 7 elementene i omkretsen?

Den positive løsningen gir for P 'samme punkt P, så det utelukkes. Den negative løsningen tilbyr definitivt koordinatene til det symmetriske punktet:

P ': (-a, -b)

Eksempel 2

Det er påkrevd å demonstrere at et AB -segment og dets symmetriske sentrale A'B 'har samme lengde.

Fra og med koordinatene til punkt A, som er (AX, AY) og de for punkt B: (BX, av), er lengden på AB gitt av:

D (ab) = √ ((bx - øks)² + (Av - ay)² )

Analogi vil det symmetriske segmentet A'B 'ha lengde gitt av:

d (a'b ') = √ ((bx' - ax ')² + (Av ' - ay')² )

Koordinatene til det symmetriske punktet a 'er øks' = -aks og ay '= -y. Tilsvarende de av b 'er bx' = -bx og av '= -by. Hvis disse koordinatene erstattes i ligningen av avstand d (a'b ') har du:

D (a'b ') = √ ((-bx + øks)² + (-By + ay)²) som tilsvarer:

 √ ((BX - AX)² + (Av - ay)²) = D (ab)

Blir demonstrert at begge segmentene har samme lengde.

Løste øvelser

- Oppgave 1

Demonstrere på en analytisk måte at den sentrale symmetriske eller en sirkel av radius r og sentrum eller, er den samme originale omkretsen.

Løsning

Ligningen av en radius r og midtsirkel (0,0) er:

x² + og² = R² (Omkretsligning C)

Hvis det på hvert punkt p i omkretsen og koordinatene (x, y) dens symmetriske koordinat p ') blir funnet, er ligningen for den symmetriske omkretsen:

x '² + og'² = R² (Symmetrisk omkretsligning C ')

Nå viser vi til resultatet av eksempel 1, som konkluderer med at koordinatene til et punkt P ', symmetrisk til P og koordinater (a, b), er (-a, -b). 

Men i denne øvelsen har punkt P koordinater (x, y), så den symmetriske p 'vil ha koordinater x' = -x e y '= -y. Å erstatte dette i den symmetriske omkretsligningen er:

Kan tjene deg: Rhomboid: Kjennetegn, hvordan ta ut omkretsen og området

(-X)² + (-og)² = R²

Som tilsvarer: x²+ og² = R², Å konkludere med at den sentrale symmetriske av en sirkel med hensyn til sentrum er selve omkretsen.

- Oppgave 2

Demonstrere på en geometrisk måte at sentral symmetri bevarer vinklene.

Løsning

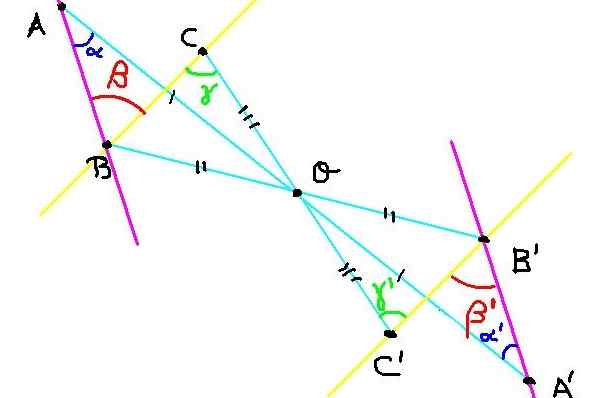Figur 4. Konstruksjon av symmetriske punkter for oppgave 2. Kilde: f. Zapata.

Det er tre punkter A, B og C på flyet. Dets symmetriske A ', B' og C 'er bygget med hensyn til symmetri -sentrum eller, som vist i figur 4. 

Nå må vi demonstrere at vinkelen ∡abc = β har samme mål som vinkelen ∡a'b'c '= β' '.

Som C og C 'er symmetriske, så oc = oc'. Tilsvarende ob = ob 'y oa = oa'. På den annen side er vinkelen ∡boc = ∡b'oc 'for å være imot toppunktet.

Da er trekantene BOC og B'OC 'kongruente for å ha en lik vinkel mellom to sider like.

Fordi BOC er kongruent med B'oc 'så vinklene  γ og γ ' De er like. Men disse vinklene, i tillegg til å oppfylle γ = γ ' De er interne alternativ mellom BC- og B'C -linjene som innebærer at BC -linjen er parallell med B'c '.

Tilsvarende er baa kongruent med b'oa 'av det som følges det α = α ' . Men  α og α ' De er indre alternative vinkler mellom BA- og B'a '-linjene, hvorav det konkluderes med at linjen BA er parallell med B'a'.

Ettersom vinkelen ∡Abc = β har sine parallelle sider med vinkelen ∡a'b'c '= β' og også begge er akutte, konkluderes det med at:

∡Abc = ∡a'b'c '= β = β' '

Demonstrerer på denne måten at sentralsymmetri beholder målet på vinkler.

Referanser

1. Baldor, J. TIL. 1973.Flat og romgeometri. Sentralamerikansk kulturell. 
2. Matematiske lover og formler. Vinkelmålingssystemer. Hentet fra: Ingemecanica.com.
3. Wentworth, g. Planetgeometri. Gjenopprettet fra: Gutenberg.org.
4. Wikipedia. Sentral symmetri. Gjenopprettet fra: er.Wikipedia.com
5. Wikipedia. Transportør. Gjenopprettet fra: er.Wikipedia.com
6. Zapata f. Interne og eksterne konjugatvinkler. Hentet fra: Lifer.com