Interne og eksterne konjugerte vinkler eksempler, øvelser

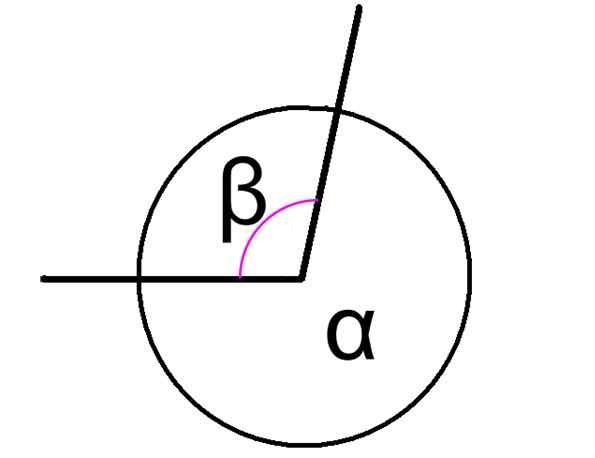
De konjugerte vinkler Det er de som er lagt til som et resultat av 360 °, uavhengig av om disse vinklene er tilstøtende eller ikke. Figur 1 viser to konjugerte vinkler, betegnet som α og β.

I så fall har vinklene α og β av figuren et felles toppunkt og deres sider er vanlige, derfor er de ved siden av. Forholdet mellom dem uttrykkes som følger:

α + β = 360º

Figur 1. To konjugerte sentrale vinkler, sum. Kilde: Wikimedia Commons. Ingen maskinlesbar forfatter gitt. Thiago R Ramos antok (basert på krav om opphavsrett)). [CC By-SA 3.0 (http: // creativecommons.Org/lisenser/by-SA/3.0/)] det er en klassifisering av vinklene med summen. Andre viktige definisjoner inkluderer komplementære vinkler, hvis sum er 90 º og Supplerende vinkler, som utgjør 180 º.

På den annen side, la oss nå vurdere to parallelle linjer kuttet av en sikring, hvis disposisjon er vist da:

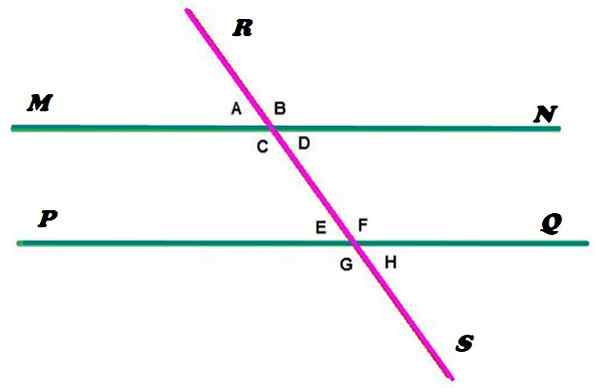
Figur 2. Parallelle linjer kuttet av en secant. Kilde: f. Zapata.

MN- og PQ -linjene er parallelle, mens RS -linjen tørker, krysser paralleller i to punkter. Som det kan sees, bestemmer denne konfigurasjonen dannelsen av 8 vinkler, som den er betegnet med små bokstaver.

Vel, i henhold til definisjonen gitt i begynnelsen, er vinklene A, B, C og D konjugert. Og på samme måte er de e, f, g og h, siden begge saker er oppfylt det:

A+B+C+D = 360º

OG

E+F+G+H = 360º

For denne konfigurasjonen er to vinkler konjugert hvis de er på samme side med hensyn til RS -tørkelinjen og begge er interne eller eksterne. I det første tilfellet er det snakk om vinkler Interne konjugater, Mens de er i det andre, er de vinkler Eksternt konjugat.

[TOC]

Eksempler

I figur 2 er de ytre vinklene de som er utenfor regionen avgrenset av MN- og PQ -linjene, det er vinklene A, B, G og H. Mens vinklene som er mellom de to linjene er C, D, E og F.

Kan tjene deg: Coplanares Points: Ligning, eksempel og løste øvelser

Nå er det nødvendig å analysere hvilke vinkler som er til venstre og hvilke til høyre for sekant.

Til venstre for RS er vinkler A, C, E og G. Og til høyre er B, D, F og H.

Vi fortsetter umiddelbart med å bestemme parene av konjugerte vinkler, i henhold til definisjonen gitt i forrige seksjon:

-A og G, ekstern og til venstre for Rs.

-D og f, internt og til høyre for Rs.

-B og H, ekstern og til høyre for Rs.

-C og E, internt og til venstre for Rs.

Eiendom av konjugerte vinkler mellom parallelle linjer

De konjugerte vinklene mellom parallelle linjer er supplerende, det vil si summen deres er lik 180 °. På denne måten, for figur 2, er følgende oppfylt:

A + g = 180º

D + f = 180º

B + H = 180º

C + E = 180º

De tilsvarende vinklene par for parallelle linjer

De er de som er på samme side av tørkelinjen, de er ikke tilstøtende og en av dem er internt og den andre er eksterne. Det er viktig å visualisere dem, siden deres tiltak er det samme, fordi de er motsatte vinkler av toppunktet.

Tilbake til figur 2 er de tilsvarende vinklene identifisert som:

-A og e

-C og g

-B og f

-D og h

Interne vinkler på en firkantet

Kvadrilateralsene er 4 -sidige polygoner, inkludert kvadratet, rektangelet, trapes, for eksempel parallellogram og rhombus, for eksempel for eksempel. Uansett form, i noen av dem, blir det oppfylt at summen av dens indre vinkler er 360º, derfor overholder de definisjonen gitt i begynnelsen.

La oss se på noen eksempler på firedoblinger og hvordan du beregner verdien dens interne vinkler i henhold til informasjonen til de foregående seksjonene:

Kan tjene deg: Hva er de 7 elementene i omkretsen?

Eksempler

a) Tre av vinklene til et firedelt mål 75º, 110º og 70º. Hvor mye skal den gjenværende vinkelmålet?

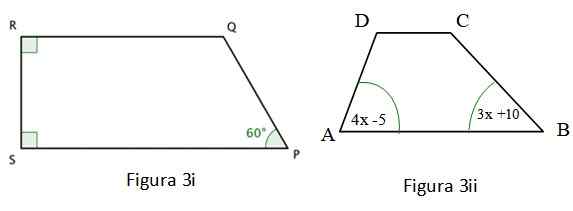
b) Finn verdien av vinkelen ∠Q i figur 3 i.

c) Beregn hvor mye målinger vinkelen ∠A i figur 3 II.

Løsning på

La α være den manglende vinkelen, det er oppfylt at:

α + 75 º + 110º + 70º = 360 → α = 105º

Løsning b

Figur 3i vist er en Trapezoid Og to av dens indre vinkler er rette, som har blitt påpekt med en fargedeplass i hjørnene. For denne kvadrilaterale er følgende bekreftet:

∠R + ∠S + ∠P + ∠Q = 360º; ∠S = ∠R = 90º; ∠P = 60º

Derfor:

∠ Q = 2 x 90º + 60º = 240º

Løsning c

Den firkantede av figur 3 II er også en trapes, som følgende er oppfylt for:

∠A + ∠B + ∠C + ∠D = 360º

Derfor:

4x -5 + 3x + 10 +180 = 360

7x + 5 = 180

X = (180 - 5) / 7

x = 25

For å bestemme vinkelen som blir bedt om i uttalelsen, brukes det at ∠A = 4x - 5. Bytte ut verdien til X tidligere beregnet, blir det fulgt at ∠A = (4 × 25) -5 = 95º

Øvelser

- Oppgave 1

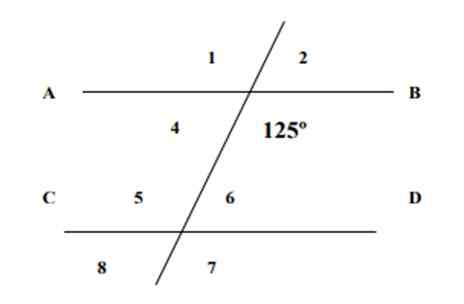
Å vite at et av vinklene som er vist er verdt 125, å finne tiltakene for de resterende 7 vinklene i følgende figur og rettferdiggjøre svarene.

Figur 4. Linjene og vinklene i trening 1. Kilde: f. Zapata.

Løsning

Vinkel 6 og vinkel 125 er internkonjugat, hvis sum er verdt 180º, i henhold til eiendommen til de konjugerte vinklene, derfor:

∠6 + 125º = 180º → ∠6 = 180º - 125º = 55º

På den annen side er ∠6 og ∠8 motsatte vinkler av toppunktet, hvis mål er det samme. Derfor måler ∠8 55º.

Kan tjene deg: vektor algebra

Vinkelen ∠1 er også motarbeidet av toppunktet ved 125, da kan vi bekrefte at ∠1 = 125º. Vi kan også appellere til det faktum at de tilsvarende vinklene par har samme tiltak. I figuren er disse vinklene:

∠7 = 125 °

∠2 = ∠6 = 55 °

∠1 = ∠5 = 125º

∠4 = ∠8 = 55 °

- Oppgave 2

Finn verdien av x i følgende figur og verdiene i alle vinkler:

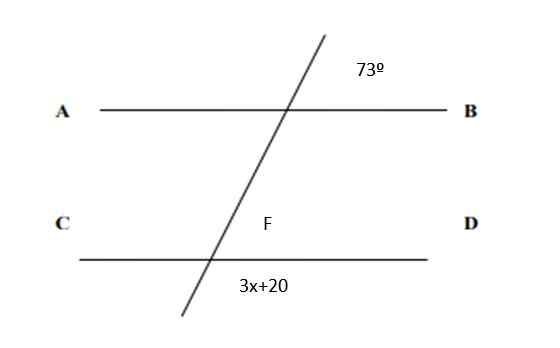Figur 5. Linjer og vinkler for trening 2. Kilde: f. Zapata.

Løsning

Siden de er tilsvarende par, følger det at F = 73º. Og på den annen side er summen av de konjugerte parene 180 º, derfor:

3x + 20º + 73º = 180º

3x = 180º - 73º -20º = 87

Endelig er verdien av x:

x = 87/3 = 29

Når det gjelder alle vinkler, vises de oppført i følgende figur:

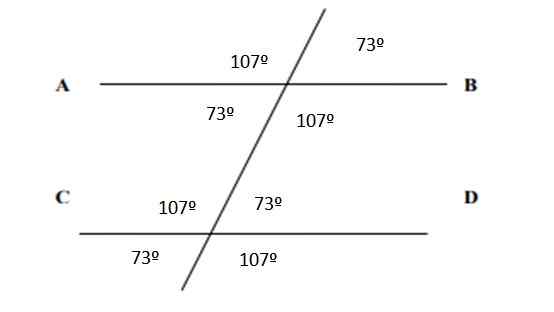Figur 6. Vinkler som resulterer i oppgave 2. Kilde: f. Zapata.

Referanser

1. Vinkelgrupper. Komplementære, supplerende og eksplisjonsvinkler Forklaring. Gjenopprettet fra: Thisiget.com/
2. Baldor, a. 1983. Flat og rom og trigonometri geometri. Kulturell hjemlandsgruppe.
3. Corral, m. Matematikk librettexts: vinkler. Gjenopprettet fra: Matematikk.Librettexts.org.
4. Mathmania. Klassifisere og konstruere vinkler ved måling. Gjenopprettet fra: Matemania.com/
5. Wentworth, g. Planetgeometri. Gjenopprettet fra: Gutenberg.org.
6. Wikipedia. Konjugerte vinkler. Gjenopprettet fra: er.Wikipedia.org.