Coplanares peker ligning, eksempel og løste øvelser

De Coplanares poeng De tilhører alle det samme flyet. To punkter er alltid koplaner, siden disse punktene definerer en linje som flat uendelig passerer. Deretter tilhører begge punktene hver av planene som går gjennom linjen og vil derfor alltid være koplaner.

På den annen side definerer tre punkter et enkelt plan, hvorav det følges at tre punkter alltid vil være koplaner til flyet de bestemmer.

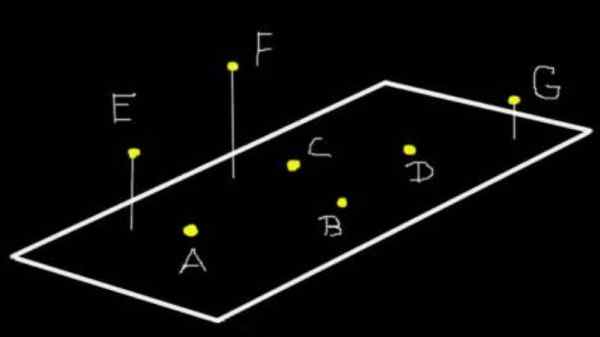
Figur 1. A, B, C og D de er koplaner til flyet (ω). E, F og G er ikke Coplanares A (ω), men hvis de er koplaner til flyet som tre definerer. Kilde: f. Zapata.

Mer enn tre poeng kan være Coplanar eller ikke. For eksempel i figur 1 er punkt A, B, C og D koplaner til flyet (ω). Men E, F og G er ikke Coplanares A (ω), selv om de er koplaner til flyet som tre definerer.

[TOC]

Ligning av et plan gitt tre punkter

Ligningen av et plan bestemt av tre kjente punkt A, B, C er et matematisk forhold som garanterer at ethvert punkt P for generiske koordinater (x, y, z) som oppfyller ligningen tilhører nevnte plan. 

Den forrige uttalelsen tilsvarer å si at hvis p av koordinat (x, y, z) oppfyller planet ligningen, vil det være at punktet vil være til Copatar med de tre punktene A, B, C som bestemte flyet.

La oss starte med å finne vektorene for å finne likningen av nevnte plan AB og Ac:

AB = [BX - AX, BY - AY, BZ - AZ]

Ac = [CX - Ax, Cy - AY, CZ - AZ]

Vektorproduktet AB X Ac Det resulterer i en vinkelrett eller normal vektor til planet bestemt av punktene A, B, C.

Et hvilket som helst punkt med koordinater (x, y, z) tilhører planet hvis det er sant at vektoren Ap er vinkelrett på vektoren AB X Ac, som er garantert hvis det er oppfylt:

Kan tjene deg: Decagon: vanlige, uregelmessige, egenskaper, eksempler

AP • (AB X AC) = 0

Dette tilsvarer å si at det tredobbelte produktet av Ap, AB og Ac Vær null. Den forrige ligningen kan skrives på en Matrix -måte:

Eksempel

La punktene A (0, 1, 2); B (1, 2, 3); C (7, 2, 1) og D (til, 0, 1). Hvilken verdi skal ha til slik at de fire punktene er Coplanares?

Løsning

For å finne verdien av A er det nødvendig at punktet D er en del av planet bestemt av A, B og C, som er garantert hvis flyligningen oppfyller.

Utvikle determinanten vi har:

A (-1-1) + 1 (-1 -7) -1 (1 -7) = -2a -8 + 6 = -2a -2 = 0

Den forrige ligningen indikerer at A = -1 For å oppfylle likhet. Med andre ord, den eneste måten som punkt D (til, 0.1) være koplanar med punktene A, B og C er at til Valga -1. Ellers vil det ikke være koplanar.

Løste øvelser

- Oppgave 1

Et plan skjærer de kartesiske aksene x, y, z i henholdsvis 1, 2 og 3. Skjæringspunktet mellom nevnte plan med aksene bestemmer punkt A, B og C. Finn DZ -komponenten i et punkt D, hvis kartesiske komponenter er:

 D (-dz, dz+1, dz) 

Under forutsetning av at D er koplanar med punkt A, B og C. 

Løsning

Når avskjæringen av et plan med de kartesiske aksene er kjent, kan den segmentale formen for planet ligning brukes:

x/1 + y/2 + z/3 = 1

Ettersom punkt D må tilhøre det forrige flyet, må du:

-DZ/1 + (DZ + 1)/2 + DZ/3 = 1

Det er å si:

-DZ + DZ/2 + ½ + DZ/3 = 1

DZ (-1 + ½ + ⅓) = ½ 

DZ (-1/6⅙) = ½ 

DZ = -3 

Fra det ovennevnte følger det at punkt D (3, -2, -3) er å koble med punktene A (1, 0, 0); B (0, 2, 0) og C (0, 0, 3).

Det kan tjene deg: Triangulous likhetskriterier

- Oppgave 2

Bestem om poeng A (0, 5, 3); B (0, 6, 4); C (2, 4, 2) og D (2, 3, 1) er Coplanares.

Løsning

Vi danner matrisen hvis rekker er koordinatene til D-A, B-A og C-A. Da beregnes determinanten og det blir bekreftet om null eller ikke.

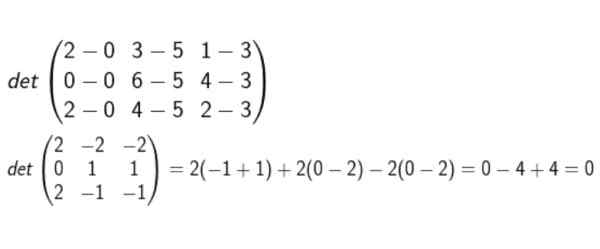
Etter å ha utført alle beregningene, er det konkludert med at de er Coplanares.

- Øvelse 3

To linjer er gitt i verdensrommet. En av dem er linjen (r) hvis parametriske ligning er:

(R): x = 1 + 2 λ; y = 1 - λ; Z = 1

Og den andre er linjen (e) hvis ligning er:

(S): x + 2 y = 1; Z = -1

Demonstrere at (r) og (e) de er koplanarium rette, det vil si at de er i samme plan.

Løsning

La oss starte vilkårlig to punkter på linjen (R) og to på linjen (e):

Rett (r): λ = 0; A (1, 1, 1) og λ = 1; B (3, 0, 1)

La oss gjøre x = 0 på linjen (e)=> y = ½; C (0, ½, -1). Og på den annen side, hvis vi gjør det y = 0 => x = 1; D (1, 0, -1).

Det vil si at vi har tatt punkt A og B som tilhører linjen (R) og punktene C og D som tilhører linjen (er). Hvis disse punktene er Coplanares, vil de to linjene også være.

Nå velger vi å peke a hvordan pivoten og så finner vi koordinatene til vektorene AB, Ac og Annonse. På denne måten får du:

B - A: (3-1, 0 -1, 1 - 1) => AB= (2, -1, 0)

C -a: (0-1, 1/2 -1, -1 -1) => Ac= (-1, -1/2, -2)

D -a: (1-1, 0 -1, -1 -1) => Annonse= (0, -1, -2)

Neste trinn er å bygge og beregne determinanten hvis første rad er vektorkoeffisientene AB, Den andre raden er den av Ac og den tredje raden av vektoren Annonse:

Kan tjene deg: Miletus slikt teorem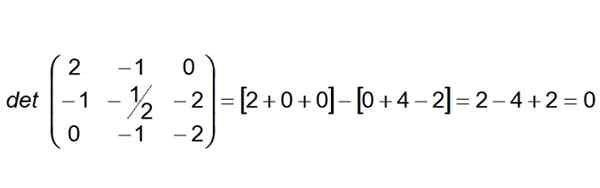

Som determinanten viser seg å være null, kan vi konkludere med at de fire punktene er Coplanarios. I tillegg kan det sies at linjer (r) og (er) også er koplaner.

- Oppgave 4

Linjene (r) og (e) er koplaner, som demonstrert i oppgave 3. Finn ligningen på flyet som inneholder dem.

Løsning

Punkter A, B, C definerer fullstendig det planet, men vi vil pålegge et hvilket som helst punkt X med koordinater (x, y, z) tilhører det samme.

X - a: (x -1, y -1, z - 1) => Øks= (X -1, y -1, z -1)

B - A: (3-1, 0 -1, 1 - 1) => AB= (2, -1, 0)

C -a: (0-1, 1/2 -1, -1 -1) => Ac= (-1, -1/2, -2)

Slik at x tilhører planet definert av a, b, c og der linjene (r) og (er) er inneholdt, er det nødvendig at determinanten dannes i sin første rad blir annullert av komponentene i Øks, i det andre av de av AB Og i det tredje av de av Ac:

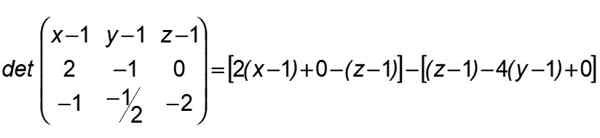
Etter dette resultatet grupperer vi på denne måten:

2 (X-1) + 4 (Y-1) -2 (z-1) = 0

Og umiddelbart ser man at det kan skrives om slik:

x - 1 + 2y - 2 - z + 1 = 0

Derfor er x + 2y - z = 2 ligningen på planet som inneholder linjene (r) og (s).

Referanser

1. Fleming, w. 1989. Prealculus matematikk. Prentice Hall Ptr.
2. KOLMAN, f. 2006. Lineær algebra. Pearson Education.
3. Lojal, j. M. 2005. Flat analytisk geometri. Mérida - Venezuela: Venezuelansk redaksjon C. TIL.
4. Navarro, Rocio. Vektorene. Gjenopprettet fra: Bøker.Google.co.gå.
5. Pérez, ca. D. 2006. Forkalkning. Pearson Education.
6. Prenowitz, w. 2012. Grunnleggende konsepter av geometri. Rowman & Littlefield.
7. Sullivan, m. 1997. Forkalkning. Pearson Education.