Vinkler i omkretstyper, egenskaper, øvelser løst

Kalt Omkretsvinkler til de der noen av dens elementer er eller krysser en gitt omkrets. Blant dem er følgende:

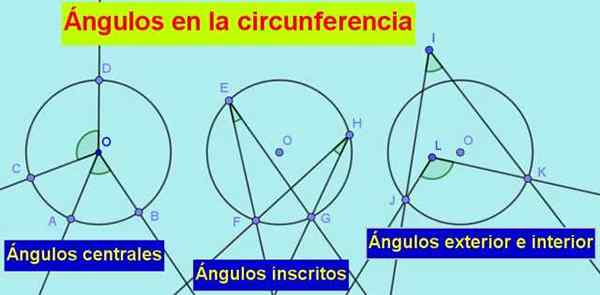
1.- Han Sentral vinkel, hvis toppunkt er i midten av omkretsen og sidene tørker til den, som vi ser i følgende bilde:

Figur 1. Typene av vinkler i omkretsen er: det sentrale, det innskrevne, det ytre og interiøret. Kilde: f. Zapata.

2.- Han Registrert vinkel, hvis toppunkt er på omkretsen og sidene er tørre eller tangente til omkretsen.

3.- Ytre vinkel, hvis toppunkt er utenfor omkretsen, men sidene er tørre eller tangente til omkretsen.

4.- Han Indre vinkel, med toppunktet inne i omkretsen og dens tørre sider til det samme.

Alle disse vinklene holder visse forhold til hverandre, og dette fører oss til viktige egenskaper mellom vinklene som tilhører en gitt omkrets.

[TOC]

Egenskaper

- Sentral vinkel

Den sentrale vinkelen er definert som den hvis toppunkt er i midten av omkretsen og sidene kuttet i omkretsen.

Radianene mål på en sentral vinkel er kvotienten mellom buen som undergir, det vil si omkretsbuen mellom sidene av vinkelen og omkretsens radius. 

Hvis omkretsen er enhetlig, det vil si radius 1, er målet på den sentrale vinkelen lengden på buen, som tilsvarer antall radianer.

Hvis du vil ha målet på den sentrale vinkelen i grader, multipliseres tiltaket i radianer etter faktor 180º/π.

Vinklene måleinstrumenter, for eksempel transportøren og goniometeret, bruker alltid en sentral vinkel og lengden på den subtitterte buen.

Kan tjene deg: Delvis derivater: egenskaper, beregning, øvelser

De er kalibrert i sexagesimale grader, noe som betyr at når en vinkel måles med dem, er det i ryggen det som måles, lengden på buen underlagt den sentrale vinkelen.

Eiendom

Målet på en sentral vinkel i radianer er lik lengden på buen som underlag eller avskjæringer delt på radiuslengden.

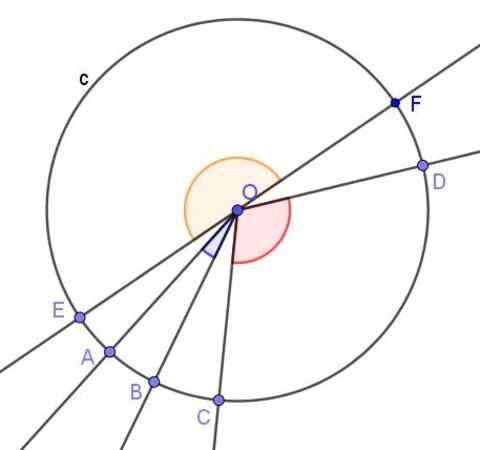Figur 2. Tre sentrale vinkler vises. Den ene akutt, den andre stump og den ene leiligheten. Kilde: f. Zapata.

- Registrert vinkel

Den registrerte vinkelen på en omkrets er en som har sin toppunkt på omkretsen og dens halvtett er tørr eller tangent til samme. 

Egenskapene er:

Egenskaper

-Den registrerte vinkelen er konveks eller flat.

-Når en innskrevet vinkel avskjærer samme bue som den sentrale vinkelen, vil målet for den første være halvparten av den andre.

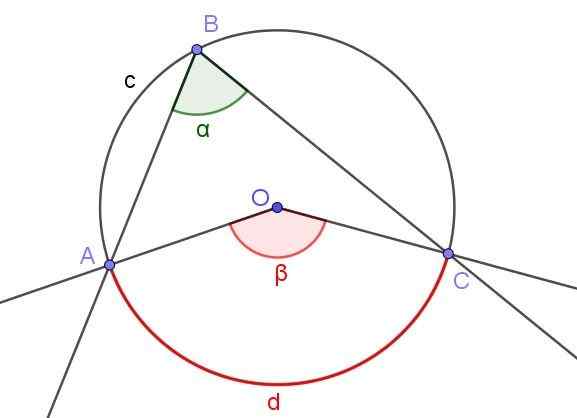Figur 3. Registrert vinkel ∠ABC og Central Angle ∠AOC som subtitter den samme buen A⌒C. Kilde: f. Zapata.

Figur 3 viser to vinkler ∠ABC og ∠AOC som avskjærer den samme omkretsbuen A⌒C.

Hvis målet på den registrerte vinkelen er α, er β -målet på den sentrale vinkelen dobbelt sånt målet på den registrerte vinkelen (β = 2 α) fordi begge trekker den samme målte bue d.

- Ytre vinkel

Det er vinkelen hvis toppunkt er utenfor omkretsen og hver av sidene kutter til omkretsen i ett eller flere punkter.

Eiendom

-Målet er lik semi -express (eller forskjell delt med 2) av de sentrale vinklene som avskjærer buene selv.

For å sikre at tiltaket er positivt, bør semi -express alltid være den sentrale vinkelen til det største målet mindre målet på den nedre sentrale vinkelen, som illustrert i følgende figur.

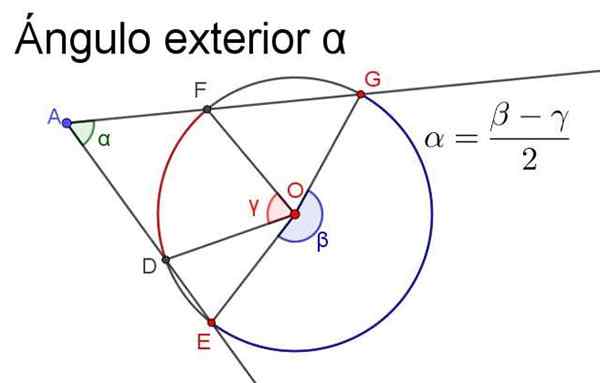Figur 4. Den ytre vinkelen α er lik halvreferansen til sentralene som underkaster de samme buene. Kilde: f. Zapata.

- Indre vinkel

Den indre vinkelen er den hvis toppunkt er inne i omkretsen og sidene kuttet til omkretsen.

Kan tjene deg: Bestemmelseskoeffisient: Formler, beregning, tolkning, eksempler

Eiendom 

Målet er lik semi -suppen i den sentrale vinkelen som sender den samme buen, pluss den sentrale vinkelen som sender den samme lysbuen som dens forlengelsesvinkel (dette er den indre vinkelen dannet av semi -straks komplementær til de av originalen indre vinkel).

Følgende figur illustrerer og tydeliggjør egenskapen til den indre vinkelen.

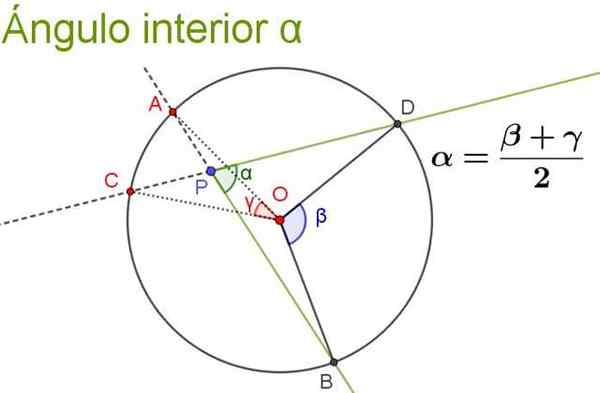Figur 5. Den indre vinkelen er lik semi -seismum i de sentrale vinklene som underkaster de samme buene som han selv. Kilde: f. Zapata.

Løste øvelser

- Oppgave 1

Anta at en innskrevet vinkel der en av sidene går gjennom midten av omkretsen, som vist i figur 6. Omkretsens radius er OA = 3 cm og buen D har en lengde på π/2 cm. Bestem verdien av α- og ß -vinkler.

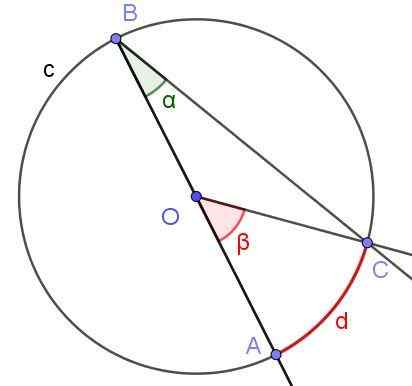Figur 6. Registrert vinkel ∠ABC med siden [BA) gjennom O og Central Angle ∠AOC.Kilde: f. Zapata.

Løsning

I dette tilfellet dannes Cob Isosceles -trianten, siden [OC] = [OB]. I en isosceles -trekant er vinklene ved siden av basen de samme, derfor må de ∠BCO = ∠ABC = α. På den annen side ∠COB = 180º - β. Tatt i betraktning summen av de interne vinklene til COB -trekanten du har:

α + α + (180º - β) = 180º

Fra hvor det følger at 2 α = β, eller hva som er ekvivalent α = β/2, som bekrefter egenskapen (3) i forrige seksjon, at målet for den registrerte vinkelen er halvparten av den sentrale vinkelen, når begge vinkler trekker fra det samme tauet [AC].

Nå fortsetter vi med å bestemme de numeriske verdiene: ß -vinkelen er sentral og dens mål i radianer er forholdet mellom buen D og radius r = OA, så dens mål er:

β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.

Kan tjene deg: firkantet: elementer, egenskaper, klassifisering, eksempler

På den annen side hadde det allerede blitt bekreftet at α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º. 

- Oppgave 2

I figur 7 vinklene α₁ og β₂ har samme mål. I tillegg vinkelen β₁ Den måler 60º. Bestemme vinklene β og α.

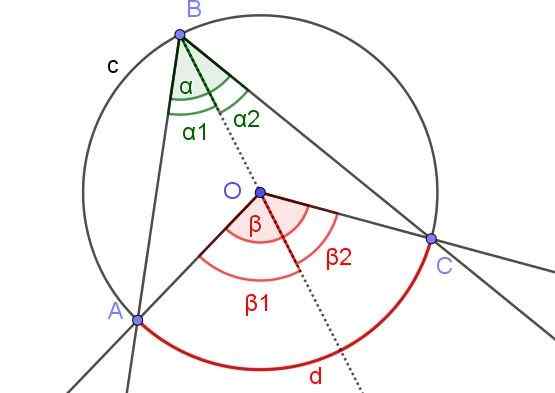Figur 7. I figur α₁ = β₂ og β₁ = 60º. Bestem verdiene til β og α. Kilde: f. Zapata.

Løsning

I dette tilfellet er det en innskrevet vinkel ∠ABC der sentrum eller omkretsen er inne i vinkelen.

På grunn av eiendom (3) har du α₂ = β₂ /2 og α₁ = β₁ /2. Som:

α = α₁ + α₂ og β = β₁ + β₂

Du har derfor:

α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Det vil si i henhold til egenskapene:

α = β / 2

Som vi blir fortalt at β₁ = 60º da:

α₁ = β₁ / 2 = 60º / 2 = 30º.

De forteller oss også at α₁ = β₂ Så det følger det:

β₂ = 30º.

Vinkelen β er:

β₁ + β₂ = 60º + 30º = 90º.

Og som α = β / 2, da:

α = 90º / 2 = 45º. 

For å konkludere:

β = 90º og α = 45º.

Referanser

1. Baldor, a. 1973. Geometri og trigonometri. Sentralamerikansk kulturell redaksjon.
2. OG. TIL. 2003. Geometrielementer: med øvelser og kompassgeometri. University of Medellin.
3. Geometri 1st. Vinkler i omkretsen. Gjenopprettet fra: Edu.Xunta.er.
4. All vitenskap. Løste øvelser med vinkler i omkretsen. Gjenopprettet fra: Francesphysics.Blogspot.com
5. Wikipedia. Registrert vinkel. Gjenopprettet fra: er.Wikipedia.com