Forklaring av andre balanser, eksempler, øvelser

De Andre likevektstilstand Den slår fast at summen av dreiemomentene eller øyeblikkene produsert av alle kreftene som virker på et organ, uavhengig av hvilket punkt som beregnes, må annulleres slik at den nevnte kroppen er i statisk eller dynamisk likevekt.

Betegner dreiemomentet eller maktmomentet gjennom det greske bokstaven τ, Matematisk uttrykkes det som følger:

∑ τ = 0

Figur 1. For å balansere rockeren er det nødvendig å bruke den andre likevektstilstanden. Kilde: Pxhere.

Den dristige bokstaven indikerer øyeblikkets vektorens natur, som må annulleres med hensyn til et hvilket som helst punkt som er valgt som et spinnsenter. På denne måten, kansellering av netto dreiemomentet, er det garantert at objektet ikke begynner å snu eller snu.

Imidlertid, hvis objektet allerede roterte tidligere, og nettomomentet forsvinner plutselig, vil rotasjonen fortsette, men med konstant vinkelhastighet.

Den andre likevektstilstanden brukes i forbindelse med den første tilstanden, som sier at summen av kreftene på et legeme må være ugyldig, slik at den ikke beveger seg, eller at hvis den gjør det, er den med ensartet rettlinjet bevegelse:

∑ F = 0

Begge forholdene gjelder for utvidede organer, de hvis dimensjoner er målbare. Når et objekt skal være en partikkel, gir det ingen mening å snakke om rotasjoner, og den første tilstanden som garanterer at balanse er nok.

Eksempler

Den andre likevektstilstanden blir avslørt i utallige situasjoner:

Når du klatrer opp trappene

Når vi støtter en trapp på gulvet og veggen, trenger vi nok til å gni, spesielt på gulvet, for å sikre at trappen ikke glir. Hvis vi prøver å klatre på en stige som støttes på et fet, vått eller glatt gulv, er det ikke vanskelig å forutse at vi vil falle.

For å kunne bruke trappen selvsikker, er det nødvendig at den er i statisk likevekt mens du klatrer og når det er i trinnet som er nødvendig.

Det kan tjene deg: Pluto (dvergplaneten)

Flytte et skap

Når du vil flytte et høye møbler som et skap, eller ethvert stykke hvis høy av å snu og legge seg ned.

Under slike omstendigheter er møblene ikke nødvendigvis i likevekt, da det kan flyttes raskt, men i det minste ville det ikke snu.

Balkonger

Balkongene som utmerker bygningene må bygges garanterer at selv om det er mange mennesker på toppen, snur det ikke og kollapser.

Dielektrisk i eksterne elektriske felt

Når du plasserer et dielektrisk materiale i et eksternt elektrisk felt, beveger molekylene seg og roterer for å innta en likevektsposisjon, og skaper et elektrisk felt inne i materialet.

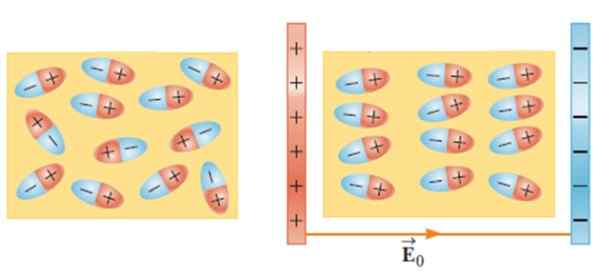Figur 2.- Uten eksternt elektrisk felt er dipolene randomisert (til venstre). Det ytre feltet bruker et dreiemoment på dielektriske molekyler, og disse blir omorganisert. Kilde: Serway, R. Fysikk for vitenskap og ingeniørfag.

Denne effekten gjør kapasiteten til en kondensator øker når et materiale som glass, gummi, papir eller olje introduseres mellom rustningen.

Skilt og lamper

Det er vanlig at mange lokaler henger varsler på bygningsveggen, slik at de er synlige for forbipasserende.

Plakaten er festet med en stang og en kabel, begge festet på veggen ved hjelp av støtter. De forskjellige kreftene som handler må sørge for at plakaten ikke faller, som de to likevektsforholdene kommer i handling.

En reflektor i en park kan også plasseres på denne måten, som i følgende figur:

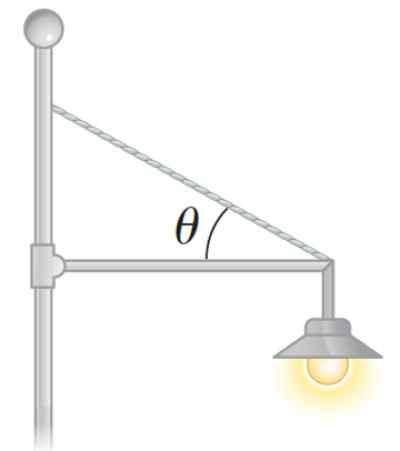Figur 3. En statisk balanselampe. Kilde: Serway. Fysikk for vitenskap og ingeniørfag.

Hvordan beregne netto dreiemomentet eller netto moment av en styrke?

Dreiemomentet eller maktmomentet, betegnet av τ enten M I noen tekster beregnes det alltid med hensyn til et punkt der rotasjonsaksen passerer.

Det er definert som vektorproduktet mellom posisjonsvektoren r, som er rettet fra nevnte akse til påføring av makt og styrke F:

Kan tjene deg: Termodynamisk balanse: Klasser og applikasjoner

τ = r × F

Å være en vektor, er det nødvendig å uttrykke dreiemomentet og gi sin størrelse, retning og mening. Størrelsen er gitt av:

τ = RF.sin θ

Riktig regel for vektorproduktet

Når problemet er i fly r, Langfingeren mot F og tommelen signaliserer inn eller ut av papiret.

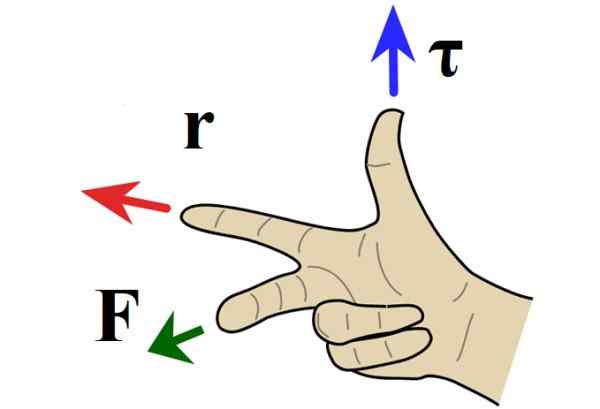Figur 4. Høyre håndregel for vektorprodukt. Kilde: Wikimedia Commons.

Når dreiemomentet peker ut av papiret, er rotasjonen i motsatt retning av klokken nåler og tildeles et positivt tegn ved konvensjon. Hvis dreiemomentet i stedet er rettet i arket, er rotasjonen i retning av hendene og negativt tegn.

For å finne nettomomentet, er det valgt et praktisk punkt for beregningen, som kan være den der den største mengden krefter fungerer. I dette tilfellet er øyeblikket til disse kreftene ugyldig, for å ha en posisjonsvektor r av størrelsesorden 0.

Du kan velge et hvilket som helst punkt som tilbyr nok informasjon til å fjerne det ukjente som ber om at problemet skal løses. La oss se det mer detaljert da.

Trening løst

Reflektoren til følgende figur har 20 kg masse og støttes av en horisontal tynnstang, med foraktelig masse og lengde L, som er artikulert til et innlegg. Kabelen, også lys, som hjelper med å opprettholde reflektoren danner en vinkel θ = 30 º med stangen. Regne ut:

a) Spenningen i kabelen

b) Størrelsen på kraften f som innlegget utøver på baren gjennom hengslet.

Løsning

Vi vil bruke den første likevektstilstanden ∑ F = 0 Til kreftene vist i diagrammet:

Kan tjene deg: Absorbert varme: Formler, hvordan du beregner det og løste øvelser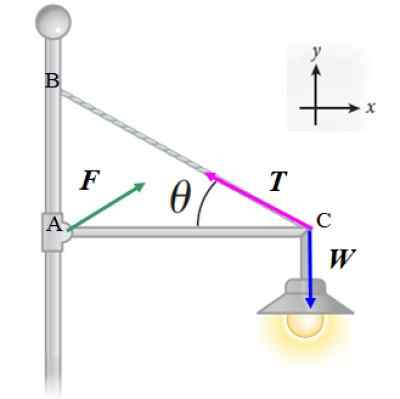

F + T + W = 0

Merk at størrelsen og retningen på F De er ennå ikke bestemt, men vi antar at det har to komponenter: f_x og f_og. På denne måten får vi to ligninger:

F_x -T. cos θ = 0

F_og - W + t⋅ sin θ = 0

La oss nå bruke den andre likevektstilstanden, velge punkt A, siden vi ikke vet størrelsen på F heller ikke det av T. Når du velger dette punktet, vektoren r_TIL er ugyldig, derfor øyeblikket av F er ugyldig og størrelsen på F Det vil ikke vises i ligningen:

-W⋅l + t⋅sen θ⋅L = 0

Derfor:

T.sin θ.L = w.L

T = w/sen θ = (20 kg x 9.8 m/s²) / Sin 30 º = 392 n

Når vi kjenner størrelsen på t, kan vi fjerne komponenten f_x:

F_x = T⋅ cos θ = 392 cos 30º n = 339. 5 n

Og deretter komponent f_og:

F_og = W - T⋅ sin θ = (20 kg x 9.8 m/s²) - 392⋅sen 30 º = 0

Da kan vi uttrykke F Så:

F = 339.5 n x

Det er derfor en horisontal kraft. Dette er fordi vi vurderer at baren hadde foraktelig vekt.

Hvis punkt C ble valgt for å beregne det resulterende øyeblikket, vektorene r_T og r_W De er null, derfor:

M = f_Y⋅L = 0

Det konkluderes med at f_og = 0. Dermed:

- W + t⋅ sin θ = 0

T = w/ sin θ

Som er det samme resultatet som opprinnelig ble oppnådd ved å velge punkt A som stedet der rotasjonsaksen passerer.

Temaer av interesse

Likevektsforhold.

Første balansetilstand.

Referanser

1. Bedford, 2000. TIL. Mekanikk for ingeniørfag: statisk. Addison Wesley.
2. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 4. Partikkelsystemer. Redigert av Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1.
5. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.