Kvantetall for hva som er bruk og hva som er

De nKvantummetre De brukes til å beskrive kvantetilstanden til elektronene i atomet og stammer fra løsningen av Schrödinger -ligningen for den enkleste av alle: hydrogenet.

Schrödingers ligning er en differensialligning, hvis løsninger er Bølgefunksjoner og de er betegnet med den greske bokstaven ψ. Uendelige løsninger kan heves, og kvadratet tilsvarer sannsynligheten for å finne elektronet i et lite romområde, kalt orbital.

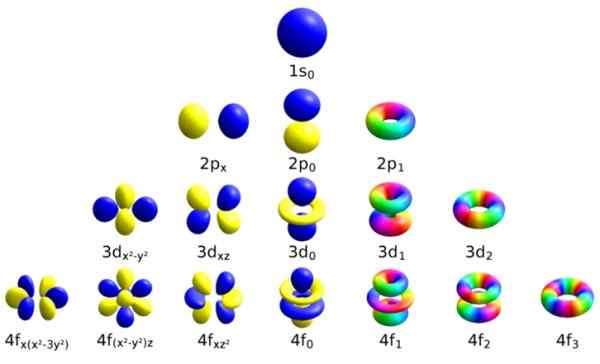
Hvert av disse atomiske orbitalene skilles ut med et visst sett med kvantetall. Kilde: Wikimedia Commons.

Hver orbital har definerte egenskaper som skiller den fra andre, for eksempel energi, vinkelmomentum og spinn, en helt kvanteegenskap til elektronet og som blant annet er ansvarlig for magnetiske effekter.

Måten å identifisere hver bane er å skille den gjennom et sett med tall som beskriver det, og dette er nettopp kvantetallene:

-N: er det viktigste kvantetallet.

-ℓ: Det azimutale kvantetallet.

-m_ℓ, Det er magnetnummeret.

-m_s, Spinnnummeret.

[TOC]

Hva er kvantetall for?

Kvantetall tjener til å beskrive tilstanden til elektroner inne i atomet. Den atommodellen der elektronet snur seg rundt kjernen er unøyaktig, fordi den ikke er i samsvar med atomstabilitet eller med et stort antall fysiske fenomener observert.

Det er grunnen til.

Senere, i 1925, reiste den østerrikske fysiske Erwin Schrödinger (1887-1961) en differensialligning i delvis derivater, hvis løsninger beskriver hydrogenatom. Er bølgefunksjonene ψ nevnt i begynnelsen.

Denne differensialligningen inkluderer de tre romlige koordinatene pluss tid, men når den ikke er inkludert, er løsningen av Schrödinger -ligningen analog med den for en stasjonær bølge (en bølge som sprer seg mellom visse grenser).

Bølgefunksjoner

Schrödingers uavhengige tidsligning er løst i sfæriske koordinater, og løsningen er skrevet som et produkt av tre funksjoner, en for hver romlig variabel. I dette koordinatsystemet, i stedet for å bruke koordinatene til de kartesiske aksene x, og og z koordinater brukes r, θ og φ. Denne måten:

Kan tjene deg: parallellkrets

ψ (r, θ, φ) = r (r) ⋅f (θ) ⋅g (φ)

Bølgefunksjonen er immateriell, til tross for kvantemekanikk forteller den oss at firkantet amplitude:

| ψ (r, θ, φ) |²

Det vil si at modulen eller den absolutte verdien av bølgefunksjonen, kvadrat, er et reelt tall som representerer sannsynligheten for å finne elektronet, i et bestemt område rundt punktet hvis koordinater er r, θ og φ.

Og dette faktum er noe mer konkret og håndgripelig.

For å finne bølgefunksjonen, må du løse tre vanlige differensialligninger, en for hver variabel r, θ og φ.

Løsningene av hver ligning, som vil være funksjonene r (r), f (θ) og g (φ), inneholder de tre første kvantetallene nevnt.

Hva er kvantetallene?

Nedenfor beskriver vi kort arten av hvert kvantetall. De tre første, som nevnt ovenfor, oppstår fra løsningene til Schrödinger -ligningen.

Det fjerde tallet ble lagt til av Paul Dirac (1902 - 1984) i 1928.

Hovedkvantumnummer

Det er betegnet av n og indikerer størrelsen på den tillatte orbitalen, så vel som elektronens energi. Jo høyere verdi, jo mer er elektronet til kjernen og energien vil også være, men til gjengjeld reduserer den stabiliteten.

Dette tallet oppstår fra r (r) funksjon, som er sannsynligheten for å finne elektronet på en viss avstand r av kjernen, som bestemmes av:

 Hvor følgende konstanter deltar:

-Planck Constant: H = 6,626 × 10 ^{-3. 4} J.s
-Elektronmasse m_og = 9.1 × 10^-31 kg
-Elektronbelastning: E ​​= 1.6 × 10^-19 C.
-Elektrostatisk konstant: K = 9 × 10 ⁹ N.m²/C²

Når n = 1 tilsvarer Bohr -radius som er verdt omtrent 5.3 × 10⁻¹¹ m.

Bortsett fra det første laget, er de andre inndelt i underkapsler eller underutstyr. Hvert lag har en energi i volt elektron gitt av:

Kan tjene deg: Mekaniske bølger: Kjennetegn, egenskaper, formler, typer

Begrepet EV "Electron Volt" betyr, energienheten som brukes ofte i området kvantefysikk. Hvor n = 1, 2, 3, 4 .. . og hver n -verdi tilsvarer en lag, som er merket med store bokstaver:

• K (n = 1)
• L (n = 2)
• M (n = 3)
• N (n = 4)
• Eller (n = 5)
• P (n = 6)
• Q (n = 7).

I teorien er det ingen øvre grense for n, men i praksis observeres det at den bare når n = 8. Minst mulig energi tilsvarer n = 1 og er den til Grunnleggende stat.

Azimutalt kvantetall eller vinkelmomentum

Betegnet med kursiv brev, bestemmer dette tallet formen på orbitalene, når du kvantifiserer størrelsen på orbital kantete momentum til elektronet.

Du kan ta hele og positive verdier mellom 0 og n-1, for eksempel:

-Når n = 1, så ℓ = 0 og det er et enkelt underutvalg.

-Hvis n = 2, kan ℓ være verdt 0 eller 1, så du har to underutstyr.

-Og hvis n = 3, antar ℓ verdier 0, 1 og 2 og det er 3 underutstyr.

Det kan følges på ubestemt tid, selv om det som nevnt før, i praksis N når opp til 8. Sub -nivåer er betegnet gjennom bokstaver: s, p, d, F og g Og de øker i energi.

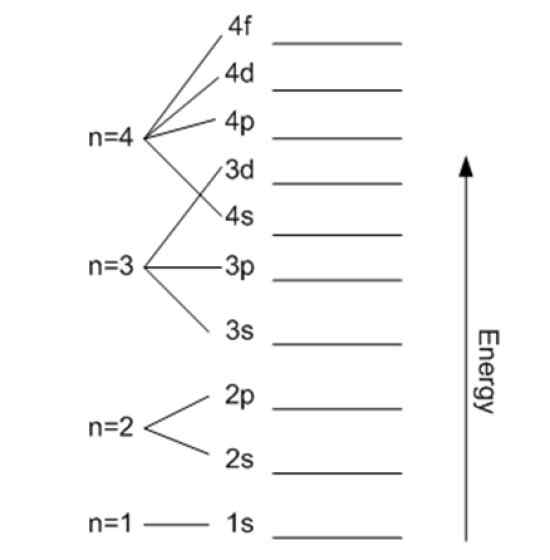Energi er relatert til det viktigste kvantetallet. Kilde: Wikimedia Commons.

Magnetisk kvantetall m_ℓ

Dette tallet bestemmer orienteringen til orbitalen i verdensrommet, avhenger av ℓ.

For en gitt ℓ er det (2ℓ+1) hele verdier av m _ℓ, Tilsvarende de respektive orbitaler. Disse er:

-ℓ, ( - ℓ+1), ... 0, ... (+ℓ -1),+ℓ.

Eksempel

Hvis n = 2, vet vi at ℓ = 0 og ℓ = 1, så m _ℓ Ta følgende verdier:

-For ℓ = 0: m _ℓ = 0.
-For ℓ = 1: m _ℓ = -1, m _ℓ = 0, m _ℓ = +1

Orbital n = 2 har to undernivåer, den første med n = 2, ℓ = 0 og m _ℓ = 0. Så har vi det andre undernivået: n = 2, ℓ = 1, med 3 orbitaler:

• N = 2, ℓ = 1, m _ℓ = -1
• N = 2, ℓ = 1, m _ℓ = 0
• N = 2, ℓ = 1, m _ℓ = +1

De tre orbitalene har samme energi, men ulik romlig orientering.

Kvantum antall spinn m_s

Når du løser Schrödinger -ligningen i tre dimensjoner, oppstår tallene som allerede er beskrevet. I hydrogen observeres imidlertid en enda ytterligere struktur enn at disse tallene ikke er nok til å forklare.

Det kan tjene deg: Gasekonstant: Hva er, beregning og eksempler

Derfor, i 1921, foreslo en annen kroppsbygning, Wolfgang Pauli, eksistensen av et fjerde nummer: spinnnummeret m_s, som tar verdier på +½ eller -½.

Med dette tallet er en veldig viktig egenskap av elektronet beskrevet, som er snurre rundt, ord som kommer fra engelsk snurre rundt (snu deg selv). Og spinnet på sin side er relatert til atomets magnetiske egenskaper.

En måte å forstå spinnet er å forestille seg at elektronet oppfører seg som en liten magnetisk dipol (en magnet med nord- og sørpoller), takket være en rotasjon rundt sin egen akse. Svingen kan være i samme retning som klokken nåler, eller i motsatt retning.

Selv om Pauli foreslo eksistensen av dette tallet, hadde resultatene av et eksperiment utført av Otto Stern og Walter Gerlach i 1922 allerede forventet det.

Disse forskerne klarte å dele en bjelke med sølvatomer ved anvendelse av et ikke -ulik magnetfelt.

Verdien av m_s Det avhenger ikke av n, ℓ og m _ℓ. Grafisk er den representert med en pil: en pil oppover indikerer timeplanen og en nedover antihoran.

Pauli -eksklusjonsprinsipp

Oppførselen til elektroner i atomet er oppsummert i prinsippet om utelukkelse av Pauli, som sier at to elektroner av et atom ikke kan eksistere i samme kvantetilstand.

Derfor må hvert elektron ha et annet sett med kvantetall n, ℓ, m _ℓ og M_s.

Betydningen av kvantetall og dette prinsippet ligger i forståelsen av egenskapene til elementene i den periodiske tabellen: elektronene er organisert i lag i henhold til N, og deretter i underkapsler i henhold til ℓ og resten av tallene.

Referanser

1. Alonso, m. 1971. Kvante- og statistiske fundamenter. Inter -amerikansk utdanningsfond.
2. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
3. Chang, R. 2013. Kjemi. 11va. Utgave. Mc Graw Hill Education.
4. Eisberg-Resnick. 1989. Kvantefysikk. Limusa - Wiley.
5. Giambattista, a. 2010. Fysikk. 2. Ed. McGraw Hill.
6. Rex, a. 2011. Fundamentals of Physics. Pearson.
7. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. McGraw Hill.