Irrasjonelle tallhistorie, egenskaper, klassifisering, eksempler

De irrasjonelle tall De er de hvis desimaluttrykk har uendelige figurer uten et repeterende mønster, derfor kan de ikke oppnås ved å gjøre kvotienten mellom to heltall.

Blant de mest kjente irrasjonelle tallene er:

Figur 1. Fra topp til bunn følgende irrasjonelle tall: PI, antall Euler, Aúrea og to firkantede røtter. Kilde: Pixabay.

Blant dem er uten tvil π (pi) den mest kjente, men det er mange flere. Alle av dem tilhører settet med reelle tall, som er det numeriske settet som samler rasjonelle og irrasjonelle tall.

Suspensive punktene i figur 1 indikerer at desimalene følger på ubestemt tid, det som skjer er at rommet til de nåværende kalkulatorene bare tillater å vise noen få.

Hvis vi ser nøye, forutsatt at vi tar kvotienten mellom to heltall, oppnås en desimal med begrensede figurer eller hvis ikke, med uendelige figurer der en eller flere blir gjentatt. Vel, dette skjer ikke med irrasjonelle tall.

[TOC]

Historie med irrasjonelle tall

Den store matematikeren til antikken Pythagoras, født i 582 til.C i Samos, Hellas, grunnla Pythagorean School of Thought og oppdaget det berømte teoremet som bærer navnet hans. Vi har det til venstre (babylonerne kunne allerede kjenne ham lenge før).

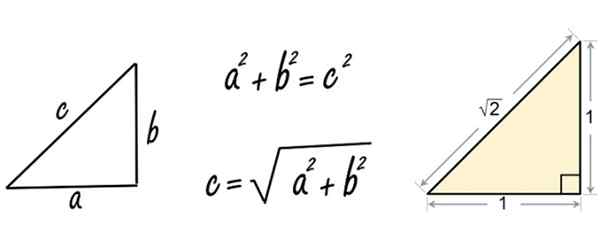Figur 2. Pythagoras teorem gjaldt en trekant av sider lik 1. Kilde: Pixabay/Wikimedia Commons.

Vel, når Pythagoras (eller sannsynligvis en disippel av ham) brukte teoremet på en høyre trekant på sider lik 1, fant det irrasjonelle tallet √2.

Det kan tjene deg: Tørkelinjer

Han gjorde det på denne måten:

C = √1² + 1² = √1+1 = √2

Og han innså umiddelbart at dette nye tallet ikke kom fra kvotienten mellom to andre naturlige tall, som var de som var kjent på den tiden.

Derfor kalte han ham irrasjonell, Og oppdagelsen forårsaket stor angst og forvirring blant pytagoreerne.

Egenskapene til irrasjonelle tall

-Settet med alle irrasjonelle tall er betegnet med bokstaven I og noen ganger som Q* eller Q^C. Forbundet mellom irrasjonelle tall I eller Q* og rasjonelle tall q, gir opphav til settet med reelle n -tall.

-Med irrasjonelle tall kan kjente aritmetiske operasjoner utføres: sum, subtraksjon, multiplikasjon, divisjon, potensering og mer.

-Inndelingen mellom 0 er ikke definert mellom irrasjonelle tall.

-Summen og produktet mellom irrasjonelle tall er ikke nødvendigvis et annet irrasjonelt tall. For eksempel:

√2 x √8 = √16 = 4

Og 4 er ikke et irrasjonelt tall.

-Summen av et rasjonelt antall pluss et irrasjonelt resulterer imidlertid i en irrasjonell. Denne måten:

1 + √2 = 2.41421356237 ..

-Produktet av et annet rasjonelt tall fra 0 med et irrasjonelt tall er også irrasjonelt. La oss se på dette eksemplet:

2 x √2 = 2.828427125 ..

-Det inverse av et irrasjonelt resulterer i et annet irrasjonelt antall. La oss prøve noen:

1 / √2 = 0.707106781 ..

1 / √3 = 0.577350269 ..

Disse tallene er interessante fordi de også er verdiene til noen trigonometriske årsaker til kjente vinkler. Mye av de trigonometriske årsakene er irrasjonelle tall, men det er unntak, for eksempel Sen 30º = 0.5 = ½, som er rasjonell.

-I summen blir de kommutative og assosiative egenskapene oppfylt. Hvis A og B er to irrasjonelle tall, betyr dette at:

Kan tjene deg: Overjektive funksjon: Definisjon, egenskaper, eksempler

A + b = b + a.

Og hvis C er et annet irrasjonelt tall, så:

(A + b) + c = a + (b + c).

-Distributive egenskapen til multiplikasjon med hensyn til summen er en annen kjent egenskap som også er oppfylt for irrasjonelle tall. I dette tilfellet:

til.(b+c) = a.b + a.c.

-En irrasjonell å ha det motsatte: -a. Når resultatet legges til, er det 0:

A+(-a) = 0

-Mellom to forskjellige rasjonelle er det minst ett irrasjonelt tall.

Plassering av et irrasjonelt tall på den virkelige linjen

Den virkelige linjen er en horisontal linje der de virkelige tallene er lokalisert, hvorav det irrasjonelle er en viktig del.

For å finne et irrasjonelt nummer på den virkelige linjen, i en geometrisk form, kan vi være verdt Pythagoras -teoremet, en regel og et kompass.

Som et eksempel skal vi lokalisere √5 på den virkelige linjen, som vi tegner et rektangelets trekant av sider x = 2 og y = 1, Som bildet viser:

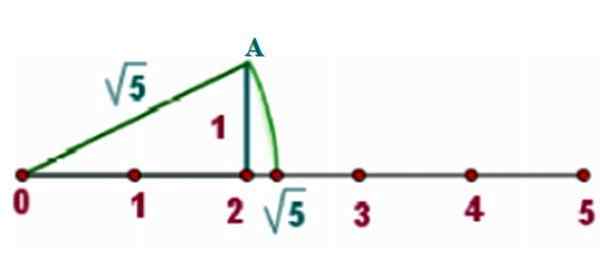Figur 3. Metode for å finne et irrasjonelt tall på den virkelige linjen. Kilde: f. Zapata.

For Pythagoras -teoremet er hypotenusen til en slik trekant:

C = √2² + 1² = √4+1 = √5

Nå er takten med spissen plassert i 0, der det også er en av toppunktene til høyre trekant. Spissen av kompass -blyanten må være i toppunktet til.

Det er tegnet en omkretsbue som kutter den virkelige linjen. Ettersom avstanden mellom omkretsen og et hvilket som helst punkt med det samme er radius, som er verdt √5, er skjæringspunktet også √5 fra sentrum.

Av grafen ser man at √5 er mellom 2 og 2.5. En kalkulator tilbyr oss den omtrentlige verdien av:

Kan tjene deg: Bestemmelseskoeffisient: Formler, beregning, tolkning, eksempler

√5 = 2.236068

Og så, å bygge en trekant med passende sider, kan andre irrasjonelle plasseres, for eksempel √7 og andre.

Klassifisering av irrasjonelle tall

Irrasjonelle tall er klassifisert i to grupper:

-Algebraisk

-Transcendent eller transcendental

Algebraiske tall

Algebraiske tall, som kan være irrasjonelle eller ikke, er løsninger av polynomligninger hvis generelle form er:

til_n xⁿ + til_N-1x^N-1 + til_N-2x^N-2 +.. . +til₁x + a_enten = 0

Et eksempel på polynomligning er en andre grads ligning som denne:

x³ - 2x = 0

Det er lett å demonstrere at det irrasjonelle tallet √2 er en av løsningene i denne ligningen.

Transcendente tall

I stedet oppstår transcendente tall, selv om det er irrasjonelt, aldri oppstår som en løsning av en polynomlig ligning.

De transcendente tallene som ofte finnes i den anvendte matematikken er π, for deres forhold til omkretsen og nummer E, eller Euler -nummeret, som er grunnlaget for de neperiske logaritmene.

Trening

På en svart firkant er en grå plassert i den posisjonen som er angitt på figuren. Det er kjent at overflaten på den svarte firkanten er 64 cm². Hvor mye er lengden på begge rutene?

Figur 4. To firkanter, hvorav lengden på sidene er å finne. Kilde: f. Zapata.

Svar

Overflaten på en kvadrat med side L er:

A = l²

Ettersom det svarte firkanten er 64 cm² av området, dens side må være 8 cm.

Dette tiltaket er det samme som Diagonalen av det grå torget. Bruke Pythagoras -teoremet på dette diagonalen, og husker at sidene av et kvadratmål måler det samme, vil vi ha:

8² = L_g² + L_g²

Hvor l_g Det er siden av det grå torget.

Derfor: 2L_g² = 8²

Påføring av kvadratrot på begge sider av likhet:

L_g = (8/√2) cm

Referanser

1. Carena, m. 2019. Preuniversity Mathematics Manual. National University of the Coast.
2. Figuera, J. 2000. Matematikk 9. plass. Grad. Co-bo-utgaver.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Utdanningsportal. Irrasjonelle tall og deres egenskaper. Hentet fra: Portaleducative.nett.
5. Wikipedia. Irrasjonelle tall. Gjenopprettet fra: er.Wikipedia.org.