Desimalnotasjon

3/2 brøkdel skrevet i desimalnotasjon

Hva er desimalnotasjon?

De desimalnotasjon Det består av å skrive et reelt tall gjennom en hel del og en desimal del, begge atskilt med et punkt eller et komma. Hele delen er igjen og desimaldelen til høyre for det punktet.

0 kan vises både i hele delen og i desimalen. Følgende tall er for eksempel desimaltall:

• 0.25
• 1.5903
• 4.19367

Merk at desimaldelen av disse tallene er endelig, men det er også tall med en uendelig desimal del, for eksempel 0.33333 ..., der suspensjonspunkter er plassert som en måte å indikere at antall desimaler fortsetter på ubestemt tid.

Generelt kan et endelig desimaltall skrives som:

N.til₁til₂til₃… til_n

Å være et heltall og n mengden desimaler, mens en uendelig desimal vedtar skjemaet:

N.til₁til₂til₃..

I desimal 0.25 er identifisert:

• N = 0
• til₁ = 2
• til₂ = 5

Desimaler oppstår som en annen måte å uttrykke rasjonelle tall på, som er de formede eller ødelagte. Faktisk kan enhver brøkdel skrives i desimalnotasjon, som det vil bli sett umiddelbart.

De tjener også til å representere tall som ikke stammer fra en brøkdel, den så -kalt irrasjonelle tall, for eksempel: π, √2, √3, √5, antallet "e" og mange andre.

Eksempler på desimaltall

Et desimaltall kan fås fra en brøkdel på en veldig enkel måte: beregning av kvotienten til telleren mellom nevneren. Hvis nevneren er enheten etterfulgt av nuller, er dette veldig enkelt:

• 8/10 = 0.8
• - (5/100) = −0.05

I det første tilfellet, ettersom nevneren er 10, plasseres desimalpunktet umiddelbart til venstre for 8 og desimal 0.8 leser "8 tideler" eller "null punkt åtte".

I det andre tilfellet, siden nevneren er 100, må du sette desimalpunktet to plasser til venstre for 5, og siden tallet er negativt, lyder det "mindre 5 hundrelapper" eller "mindre null null punkt fem".

Når nevneren ikke er enheten etterfulgt av 0, brukes den lange divisjonen:

Legg merke til at for å utføre denne divisjonen, ettersom telleren er mindre enn nevneren, ble den multiplisert først med 10 og ved å gjøre det, en 0 etterfulgt av desimalpunktet i kvotienten, for ikke å endre operasjonen, for ikke å ikke For å endre operasjonen. Fortsett deretter normalt for å dele 10 med 2 som er lik 5 og divisjonsresten er 0.

Kan tjene deg: vektorbeløp

Desimalformen av brøkdel ½ er 0.5, at "null punkt fem" leses:

Fraksjon 7/8 er et annet eksempel. Ettersom 7 er mindre enn 8, multipliserer den 7 × 10 = 70, en 0 er plassert i kvotienten etterfulgt av desimalpunktet og er normalt delt:

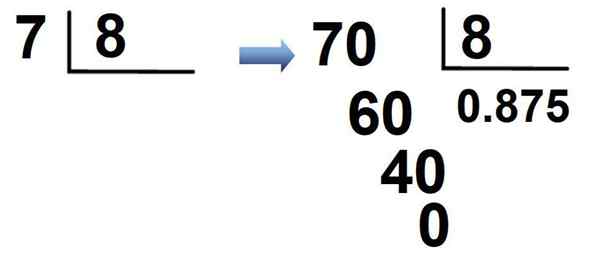
Resultatet er at brøkdelen er skrevet i desimalnotasjon som:

7/8 = 0.875

Dette tallet, som det forrige resultatet, er en begrenset desimal og en måte å lese det på er: "Zero Point Eight Hundred and Seventy -Five". Gjennom denne prosedyren er følgende brøk også skrevet i desimalnotasjon:

8/10 = 0.8

5/7 = 0.714285714 ..

9/20 = 0.Fire fem

3/8 = 0.375

Merk at som i alle disse brøkene telleren er mindre enn nevneren, er hele delen av de resulterende desimalene 0. Imidlertid et blandet tall eller en Uekte brøk (Den hvis teller er større enn denominatoren) har også desimalrepresentasjon.

I dette tilfellet er hele delen større enn eller lik 1 hvis brøkdelen er positiv, og mindre enn -1 hvis den er negativ:

9/4 = 2.25

10/3 = 3.333333 ..

−12/5 = −2.4

1 ½ = 1.5

2 ¾ = 2.75

Hele delen og brøkdelen av de negative desimalene

I de foregående eksemplene ble det observert at for å finne desimaluttrykket av en brøkdel, er en teller og nevner ganske enkelt delt. Selv om brøkdelen er negativ, blir minustegnet ganske enkelt satt til det tilsvarende desimientuttrykket.

Imidlertid er hele delen og den brøkdelte delen av en desimal forskjellig i henhold til skiltet du bærer.

Når en desimal er positiv, som 2.25, hele delen er 2 og desimaldelen er 0.25 og antallet kan skrives som summen av hele delen og desimaldelen, slik:

2.25 = 2 + 0.25

Hele delen er definert som heltallet umiddelbart lavere enn desimalet, og desimaldelen er alltid positiv. For 2.25, er det umiddelbart nedre heltallet 2.

Men i tilfelle av brøkdel −12/5, tilsvarer desimal −2.4 Ovennevnte fungerer ikke.

Kan tjene deg: Hva er delene av det kartesiske flyet?

 Hvis −2 var det hele delen, og 0.4 Desimaldelen, ved å legge til, ville bli oppnådd:

−2 + 0.4 = −1.6 ≠ −2.4

Derfor hele delen av −2.4 kan ikke være −2, men det umiddelbart nedre heltallet: −3. Men i så fall ville ikke brøkdelen være 0.4, siden ved å legge til:

−3 + 0.4 = −2.6 ≠ −2.4

Så hva er desimaldelen av det negative tallet −2.4? Det trekker desimaltallet fra hele sin del, og resultatet vil alltid være positivt:

−2.4 - ( - 3) = 0.6

Til slutt er det bevist at ved å legge til hele delen og den brøkdelte delen, oppnås den etterspurte desimalen:

−3 + 0.6 = −2.4

Prosedyren for å finne en hel del og desimal del av et hvilket som helst tall, uavhengig av tegnet, blir oppsummert på denne måten:

• Hele delen er heltallet som er lavere enn desimaltallet.
• Desimaldelen beregnes ved å trekke desimalet fra hele sin del.

Imidlertid, for praktiske beregningsformål, desimaltallet −2.4 kan brytes ned som - (2 + 0.4) = - 24/10 eller:

Som det kan sees, er ikke desimalnotasjonsrepresentasjonen av et tall unik.

Typer desimaler

Det er desimaltall hvis desimaldel er begrenset eller uendelig, som brukes som klassifiseringskriterier:

Endelige eller eksakte desimaler

Når desimalene er endelige, for eksempel 0.125, sies det også at de er Eksakte desimaler.

Uendelige desimaler

En uendelig desimal oppnås når resten av divisjonen mellom teller og nevner blir aldri laget 0.

Forutsatt at desimal kommer fra kvotienten mellom to heltall, er denne desimaldelen periodisk, det vil si at den er sammensatt av en eller flere figurer som gjentas på ubestemt tid, kalt periode.

For eksempel nummer 3.333333… Opprinnelig av den feilaktige brøkdelen 10/3, er det en periodisk desimal: hele delen er 3, og etter desimalpunktet gjentas tallet 3 på ubestemt tid på ubestemt tid. Dette kan symboliseres ved å plassere en kurve eller hatt på antallet som gjentas:

Perioden kan være et større figur, som i brøkdel 5/7, hvis representasjon i desimalnotasjon er 0.71428571428571428 ... og det er skrevet som:

Kan tjene deg: proporsjonal variasjon

Disse desimalene der perioden vises umiddelbart etter desimalpunktet kalles Rene periodiske desimaler. Imidlertid i denne andre:

Perioden, som er 45, er gitt av to sifre som ikke gjentas lenger i desimaldelen: 23. Dette tallet kalles anteperiode, Siden det går foran perioden. I dette tilfellet er det en Blandet avis desimal.

Endelig er det uendelige desimaler som ikke er aviser, som ikke stammer fra kvotienten mellom to hele tall. Som nevnt i begynnelsen, tilhører disse desimalene hele irrasjonelle tall, Som PI -nummeret, for eksempel.

Løste øvelser

Oppgave 1

Skriv numerisk følgende desimalnumre:

a) nullpunkt fire hundre førti -syv
b) Fem tusendeler
c) To enheter og fem hundrelapper
d) tre poeng tjue -syv negativt
e) ett poeng åtte hundre tjue tusen fem hundre seksti -tre

• Løsning

a) 0.447

b) 0.005

c) 2.05

d) −3.27

e) 1.824563

Oppgave 2

Klassifiser følgende desimaltall i eksakte desimaler, rene aviser, blandede aviser eller irrasjonelle tall. I alle tilfeller, angi verdien av hele delen, og hvis de er aviser eller blandede aviser, indikerer du også verdien av perioden og fremre, etter behov:

a) 0.35627

b) 1.21212121 ..

c) −1.32

d) 1.414213562 ... = √2

• Løsning

a) 35627 er en eksakt desimal. Hele delen er 0 og dens desimaldel er 0.35627.

b) 1.21212121 ... er en uendelig desimal og ren avis, hele delen er 1 og perioden er 21.

c) −1.32 er en nøyaktig og negativ desimal, hvis hele delen er −2. Desimaldelen beregnes ved å trekke desimaltallet fra hele delen:

−1.32 - (−2) = 0.68

d) Desimalt uttrykk for √2 er uendelig og ikke periodisk, siden det er et irrasjonelt tall.

Det er en blandet avis, hele delen er 3, den fremre er 1 og perioden er 89.

Referanser

1. Pedagogiske bidrag og didaktisk materiale. Desimalnotasjon. Gjenopprettet fra: TecDigital.Tec.Ac.Cr.
2. Baldor, a. 2007. Praktisk teoretisk aritmetikk. Redaksjonell gruppe Patria s.TIL. Av c.V.
3. Matematikk for handler. Forstå desimalnotasjon. Hentet fra: OpenTextBc.Ac.
4. Unam. Rasjonelle tall: betydninger og representasjoner. Gjenopprettet fra: Redi.Kode.Unam.MX.