Notasjon utviklet det som er, eksempler og øvelser
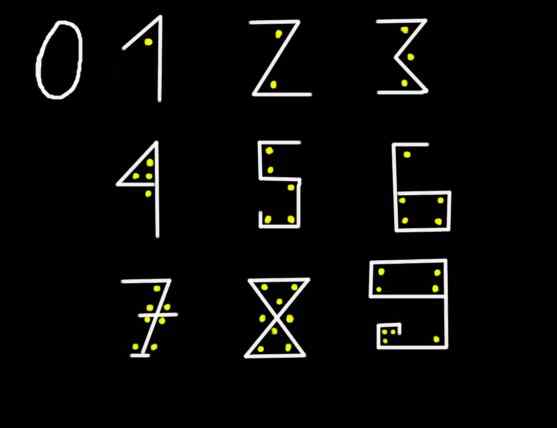
- 1803
- 318
- Prof. Oskar Aas
De utviklet notasjon Det er en der en numerisk figur uttrykkes som en sum der posisjonsverdien til hvert siffer som danner antallet er tatt i betraktning.
For eksempel når du skriver en figur som 2345, har hvert siffer av det et posisjonshierarki. Lesing av høyre ekstrem siffer til venstre, hierarkiet eller verdien vokser.
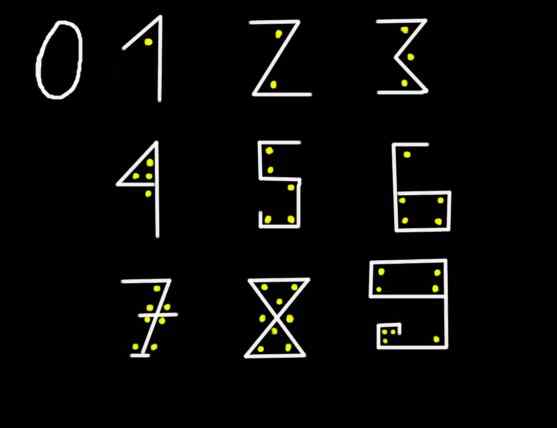 Figur 1. Med ni grafemer er det mulig å representere ethvert figur.
Figur 1. Med ni grafemer er det mulig å representere ethvert figur. I figur 2345 representerer siffer 5 fem enheter, Digit 4 representerer fire titall. Det vil si at i utviklet eller utvidet notasjon er figuren 2345 skrevet slik:
2345 = 2 tusen + 3 hundre + 4 tens + 5 enheter
Men det kan også uttrykkes som følger:
2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.
Figur 2345 kan også skrives som summen av krefter på 10:
2345 = 2 x 10^3 + 3 x 10^2 + 4 x 10^1 + 5 x 10^0
Der circumflejo ^ betyr å heve den angitte eksponenten. For eksempel 10^3 = 10 x 10 x 10 = 1000. En annen måte å skrive eksponentene på er gjennom et tilsyn:
2345 = 2 x 103 + 3 x 102 + 4 x 101 + 5 x 100
[TOC]
Posisjonell nummereringssystem
Det arabiske tallsystemet er tallene som brukes daglig i de aller fleste kontinenter og land i verden. Arabiske tall er et basesystem 10 fordi ti symboler eller grafemer brukes til å skrive et hvilket som helst tall. Disse ti symbolene er:
0 1 2 3 4 5 6 7 8 9
Med bare ett av disse symbolene kan tall mellom null til ni uttrykkes. Å uttrykke tall større enn ni, posisjonssystemet basert på ti. Figur 10 er et dusin og null enheter. Figur 11 er et dusin og en enhet. Figur 123 (hundre tjue -tre) er hundre, to titalls og tre enheter. Skrevet i form av krefter på ti nummer 123 vil være:
Kan tjene deg: 60 deling1 × 10^2 + 2 × 10^1 + 3 × 10^0
Hvor:
10^2 = 10 x 10 = 100
10^1 = 10
10^0 = 1.
Med dette eksemplet er det klart at plasseringen av sifferet til slutt er posisjon 0 og representerer antall enheter, den for det andre sifferet fra høyre til venstre er posisjon 1 og representerer antall titalls, tredje siffer (høyre til Venstre) har posisjon 2 og representerer hundrevis.
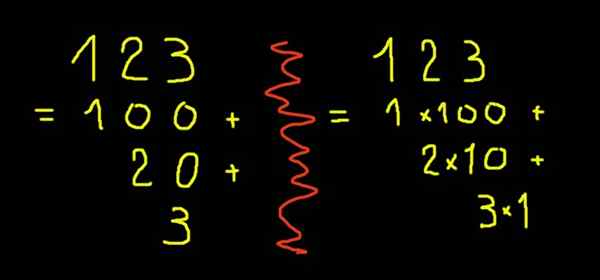 Figur 2. Utviklet notasjon av figur 123.
Figur 2. Utviklet notasjon av figur 123. Brøk- eller desimaltall
Med desimal posisjonssystem er det også mulig.
For å representere brøkdelen ½ i det arabiske desimalsystemet, det vil si at halvparten av enheten er skrevet:
½ = 0,5
For å nå dette uttrykket i systemet vårt basert på 10, er følgende operasjoner blitt utført:
1- Multipliser teller og nevner for 5 for å ha den ekvivalente fraksjonen 5/10 = 1/2.
2- Del med 10 tilsvarer å multiplisere med kraften basert på ti med eksponenten mindre (10^-1), det vil si 5/10 = 5 × 10^-1.
3- Den negative eksponenten indikerer hvor mange ganger sifferet som er angitt fra enheten til enheten er kjørt eller plassert, i vårt tilfelle ville det være 0,5.
4- ½ = 0,5 I utvidet notasjon er det skrevet slik:
0,5 = 0x10^0 + 5 × 10^-1
Der 10^-1 = 0,1 er en tidel (brøkdelen som tilsvarer enheten delt inn i 10 like deler).
På denne måten tilsvarer tallet 0,5 fem tideler, men tallet 0,05 tilsvarer 5 hundrelapper og 0,005 til 5 tusendeler.
Kan tjene deg: Hvorfor er algebra viktig i visse hverdagslivssituasjoner?Utviklede notasjonseksempler
Eksempel 1
Gitt 40201 -tallet i standardnotasjon, konverter den til den utviklede notasjonen.
Løsning:
4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 = 40201
Eksempel 2
Skriv brøkdelen ¾ i utvidet notasjon.
Løsning:
I dette tilfellet er det tre fjerdedeler av enheten.
3/4 = 15/20 = 75/100 = 0,75 = 7/10 + 5/100 =
7 × 10^-1 + 5 × 10^-2.
Sa med ord ville være slik:
Brøkdelen ¾ tilsvarer syv tideler pluss fem hundrelapper.
Utviklede notasjonsøvelser
Oppgave 1
Si med ord uttrykket utviklet av 40201 -figuren i eksempel 1.
Løsning:
Den utviklede notasjonen er slik:
40201 = 4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1
At det på ordspråk blir sagt:
Fire titusenvis, pluss tusenvis av tusenvis, pluss to hundre, flere null titalls, pluss en enhet.
Oppgave 2
Uttrykke i ordene den forrige figuren og bryte ned den tilsvarende frasen utviklet.
Løsning:
40201 -figuren i ord er uttrykt som følger:
Førti tusen to hundre en
Den forrige setningen kan utvikle seg som:
40 × 1000 + 2 × 100 + 1
Det kan sies at måten å uttale figurene er en halvutviklet måte å uttrykke det på.
Øvelse 3
Skriv nummer 7/3 utviklet måte.
Løsning:
Det er en figur uttrykt som en feil brøkdel, siden telleren er større enn nevneren, er figuren større enn enheten.
Denne upassende brøkdelen kan brytes ned som summen av brøk 6/3 + 1/3. Den første av brøkene resulterer i et helt nummer 2, mens 1/3 = 0,333333, der siffer 3 gjentas på ubestemt tid. Slik at desimaluttrykket utviklet av 7/3 -figuren alltid vil være et omtrentlig uttrykk:
Kan tjene deg: firkantet: elementer, egenskaper, klassifisering, eksempler7/3 = 2 + 1/3 ≃ 2 + 0,333 = 2 + 3 × 10^-1 + 3 × 10^-2 + 3 × 10^-3.
Oppgave 6
Skriv i standardnotasjon og utviklet deretter nummeret: Tjue -tre milliarder to hundre og femti millioner fem hundre tjue -seks tusen tre hundre tjue -fem med tre tjue -tre -tusendeler.
Løsning:
Det må huskes at en Millardo tilsvarer en milliard. Ordet Millardo Det ble akseptert av Royal Spanish Academy i 1995 etter anmodning fra avdøde Venezuelas president Rafael Caldera, medlem av det venezuelanske språkhåndverket. I så fall er figuren av standardnotasjonen skrevet som følger:
23.2501526.325.023
23 milliarder + 250 millioner + 526 tusen + 325 enheter + 23 tusendeler.
23 × 10^9 + 250 × 10^6 + 526 × 10^3 + 325 × 10^0 + 23 × 10^-3
Endelig er figuren i utviklet notasjon skrevet:
2 × 10^10 + 3 × 10^9 + 2 × 10^8 + 5 × 10^7 + 0x10^6 + 5 × 10^5 + 2 × 10^4 + 6 × 10^3 + 3 × 10^ 2 + 2 × 10^1 + 5 × 10^0 + 0x10^-1 + 2 × 10^-2 + 3 × 10^-3.
Referanser
- Khan Academy. Posisjonsverditabeller. Gjenopprettet fra: er.Khanacademy.org
- Khan Academy. Skriv et utviklet nummer (video). Gjenopprettet fra: er.Khanacademy.org
- Ifrah, Geoges (1998): Universal History of Figures. Espasa Calpe s.TIL.
- Wikipedia. Posisjonell notasjon. Gjenopprettet fra: er.Wikipedia.com
- Wikipedia. Millardo. Gjenopprettet fra: er.Wikipedia.com
- « Fosforoksyd (V) Struktur, egenskaper, innhenting, bruk, risiko
- Aluminiumfosfat (ALPO4) struktur, egenskaper, innhenting, bruk »

