Unidimensjonale bølger Matematisk uttrykk og eksempler

De Unidimensjonale bølger Det er de som forplanter seg i en retning uavhengig av om vibrasjoner oppstår eller ikke i samme utbredelsesretning. Et godt eksempel på dem er bølgen som beveger seg langs et spent tau som en gitar.

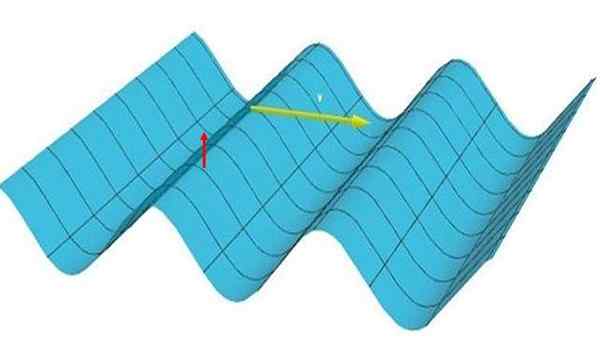
I en flat bølge kryss, Partiklene vibrerer vertikalt (de klatrer og går ned, ser den røde pilen i figur 1), men den er en -dimensjonal fordi forstyrrelsen beveger seg i en retning, etter den gule pilen.

Figur 1: Bildet representerer en endimensjonal bølge. Merk at rygger og daler danner parallelle linjer med hverandre og vinkelrett på forplantningsretningen. Kilde: Selvlaget.

Unidimensjonale bølger vises ganske ofte i hverdagen. Følgende avsnitt beskriver noen eksempler på dem og også bølger som ikke er unidimensjonale, for å tydelig etablere forskjellene.

[TOC]

Eksempler på unidimensjonale bølger og ikke -uidimensjonale bølger

Unidimensjonale bølger

Dette er noen eksempler på en -dimensjonale bølger som lett kan observeres:

- En lydpuls som reiser gjennom en rett bar, siden det er en forstyrrelse som sprer seg gjennom baren.

- En bølge som reiser gjennom en vannkanal, selv når forskyvningen av vannoverflaten ikke er parallell med kanalen.

- Bølger som sprer seg på en overflate eller gjennom det tre -dimensjonale rommet kan også være en -dimensjonal, forutsatt at bølgefrontene deres er plan parallelt med hverandre og reiser i en retning.

Ikke -dimensjonale bølger

Et eksempel på en ikke -dimensjonal bølge finnes i bølgene som dannes på en overflate av stille vann når en stein slippes. Det er en to -dimensjonal bølgefront av sylindrisk bølge.

Kan tjene deg: spakarmFigur 2. Bildet representerer et eksempel på hva som ikke er en endimensjonal bølge. Merk at rygger og daler danner sirkler og formeringsretningen er radial utover, det er da en to -dimensjonal sirkulær bølge. Kilde: Pixabay.

Et annet eksempel på dimensjonsbølge som ikke er fagforeninger er lydbølgen som genererer en fyrverkeri av eksplosjon i en viss høyde. Dette er en tre -dimensjonal bølge med sfæriske bølgefronter.

Matematisk uttrykk for en endimensjonal bølge

Den mest generelle måten å uttrykke en endimensjonal bølge som sprer seg uten demping i den positive retningen av aksen x og med hastighet v Det er matematisk:

og (x, t) = f (x - v.t)

I dette uttrykket og representerer forstyrrelsen i stillingen x Øyeblikkelig t. Bølgeformen er gitt av funksjonen F. For eksempel er bølgefunksjonen vist i figur 1:  og (x, t) = cos (x - v t) og bildet av bølgen tilsvarer øyeblikket t = 0.

En bølge som denne, beskrevet av en kosinus eller sinusfunksjon, kalles harmonisk bølge. Selv om det ikke er den eneste bølgeformen som eksisterer, er det av største betydning, fordi enhver annen bølge kan representeres som en overlapp eller sum av harmoniske bølger. Det er bekjentskap Fourier teorem, så brukt til å beskrive signaler av alle slag.

Når bølgen reiser i negativ retning av x -aksen, endres den ganske enkelt v av -v I argumentasjon, å være:

og (x, t) = g (x + v t)

Figur 3 viser animasjonen av en bølge som reiser til venstre: det er en form som kalles funksjon Lorentziana og henne Matematisk uttrykk er:

Kan tjene deg: arbeid: formel, enheter, eksempler, øvelser

og (x, t) = 1 / (1 + (x + 1⋅t)²

I dette eksemplet er hastigheten på forplantning v = 1, -en plassenhet for hver tidsenhet-.

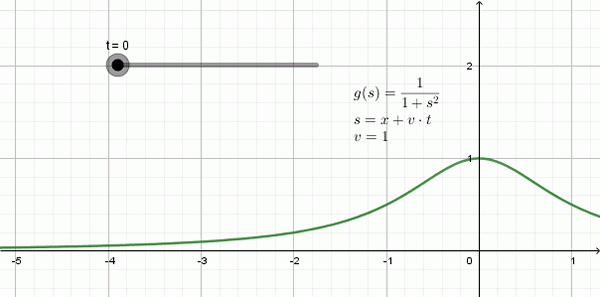Figur 3. Eksempel på en Lorentzian -bølge som reiser til venstre raskt v = 1. Kilde: Utarbeidet av F. Zapata med Geogebra.

Unidimensjonal bølge ligning

Wave -ligningen er en ligning i delvis derivater, hvis løsning selvfølgelig er en bølge. Den etablerer det matematiske forholdet mellom den romlige delen og dens tidsmessige del, og har formen:

Løsningen, som nettopp er funksjonen y (x, t), kan verifiseres ved erstatning og utvikling i denne ligningen. For eksempel funksjoner f (x - v t)  og  G (x + vt)  nevnt, de er bølge ligningsløsninger.

Løst eksempel

Så har du det generelle uttrykket y (x, t) for en harmonisk bølge:

og (x, t) = a⋅cos (k⋅x ± ω⋅t + θo)

a) Beskriv den fysiske betydningen av parametrene A, K, ω og θo.

b) Hvilken betydning har tegnene ± på argumentet fra Coseno?

c) Kontroller at det gitte uttrykket faktisk er løsningen av bølgelikningen i forrige seksjon og finn hastigheten v av forplantning.

Løsning på)

Funksjonene i bølgen er i følgende parametere:

-TIL representerer amplitude eller "bølgehøyde".

-k er i Bølgenummer Og det er relatert til bølgelengden λ gjennom K = 2π/ λ.

-Ω Det er fVinkelutvidelse Og det er relatert til periode T bølge svingning av

Ω = 2π/ t.

-θo Det er den innledende fase, som er relatert til utgangspunktet for bølgen.

Kan tjene deg: statisk friksjon: koeffisient, eksempel, trening

Løsning B)

Negativt tegn blir tatt hvis bølgen reiser i positiv retning av x -aksen og positivt tegn på annen måte.

Løsning C)

Kontroller at det gitte uttrykket er en løsning på bølge ligningen er enkel: det delvise derivatet av funksjonen tas og (x, t) Når det gjelder x to ganger, er den delvis avledet fra T to ganger, og deretter møtes begge resultatene for å oppnå likhet:

Andre avledet fra x: ∂²og/ ∂x²= -K². TIL⋅cos (k⋅x ± ω⋅t + θo)

Andre avledet fra t: ∂²og/ ∂t²= -Ω². TIL⋅cos (k⋅x ± ω⋅t + θo)

Disse resultatene erstattes i bølgeforlikningen:

 -k². TIL⋅cos (k⋅x ± ω⋅t + θo) = (1/v²) (-Ω². TIL⋅cos (k⋅x ± ω⋅t + θo))

Så mye TIL Ettersom kosinus er forenklet, siden de vises på begge sider av likhet og argumentet til kosinuset er det samme, reduseres uttrykket til:

-k² = (1/v²) (-Ω²)

Som gjør det mulig å få en ligning til v i form av Ω og k:

v² = Ω² / k²

v = ± Ω / k

Referanser

1. E-pedagogisk. Ligning av unidimensjonale harmoniske bølger. Gjenopprettet fra: e-dukativ.Katedu.er
2. Rincón of Physics. Bølgeklasser. Hentet fra: Fysikk.Blogspot.com.
3. Figueroa, d. 2006. Bølger og kvantefysikk. Serier: Fysikk for vitenskap og ingeniørfag. Redigert av Douglas Figueroa. Simon Bolivar University. Caracas Venezuela.
4. Fysikklaboratorium. Bølgebevegelse. Gjenopprettet fra: Fisicalab.com.
5. Peirce, a. Foredrag 21: The One Dimensional Wave Equation: D'Aremberts løsning. Hentet fra: UBC.Ac.
6. Bølge ligning. Hentet fra: i.Wikipedia.com