Kartesisk plan

Hva er det kartesiske flyet?

Han Kartesisk plan Den består av et par rette linjer vinkelrett på hverandre og som krysser hverandre på et tidspunkt. En av linjene er vertikal og den andre horisontale, og tar til skjæringspunktet som systemets opprinnelse.

Målet er å enkelt finne et hvilket som helst flatt punkt gjennom et par verdier: koordinering. For å gjøre dette, på hver av linjene en skala med hele tall er konstruert, er de positive skrevet i den ene retningen og negativene i den andre, som vist i følgende figur:

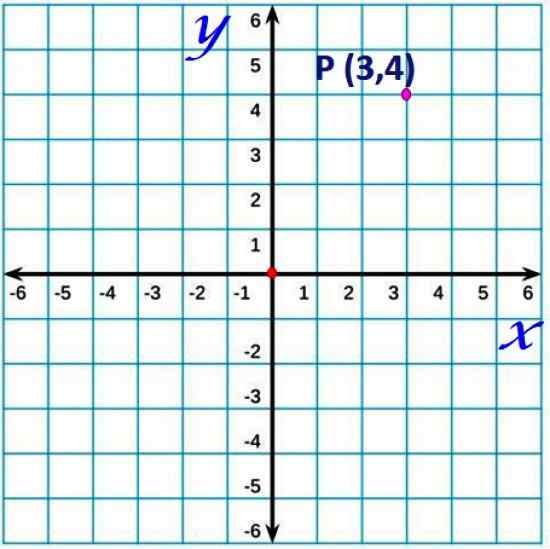
Figur 1. Et punkt i det kartesiske flyet. Kilde: f. Zapata.

Ved konvensjon kalles den horisontale aksen vanligvis x og vertikal akse som akse og.

Et hvilket som helst punkt i flyet vil ha koordinater spesifisert av et ordnet par (X, y). For eksempel punktet P for koordinat (3,4), som ligger 3 enheter til høyre for opprinnelsen og 4 enheter opp, i den øvre figuren. Det ligner på et kart, som indikerer breddegrad og lengde på et bestemt sted.

Ettersom to koordinater er nødvendige, sies det at flyet er to -dimensjonalt, men konseptet utvides lett til tre dimensjoner, og legger til en mer koordinatakse, som vanligvis betegnes som Z -akse. I dette tilfellet tar koordinater form (X og z).

Det kartesiske flyet mottar navnet sitt fra den franske forskeren René Descartes (1596-1650), som formaliserte det i sitt arbeid Metode tale av 1637, selv om det er en historie i verkene til Apollonius av Perga (262-190 AC), matematikeren som oppdaget de koniske kurvene: omkrets, ellipse, lignelse og hyperbola.

Kan tjene deg: Cubes Difference: Formler, ligninger, eksempler, øvelser

Kjennetegn på det kartesiske planet

- Som han X akse Som Axis y De strekker seg uendelig i begge ender, og krysser sammen vinkelrett (i en vinkel på 90 grader). Denne funksjonen kalles ortogonalitet.

- Punktet der begge aksene krysser hverandre er kjent som opprinnelse eller nullpunkt.

- Koordinatsystemet deler flyet inn i fire regioner kalt kvadranter.

- Steder i koordinatplanet er beskrevet som bestilte par.

- Hvert punkt på det kartesiske planet er assosiert med en unik x -koordinat og en koordinat og unik.

Elementer i det kartesiske flyet

Elementene i det kartesiske planet er følgende:

-De Numeriske linjer enten koordinere akser x og y, Hvis det er flyet. Aksen og motta aksenavnet på ordinene, mens aksen x Det er Abscissa -aksen. Når det gjelder verdensrommet, blir aksen lagt til z, i stand til å representere både høyde og dybde.

-Han opprinnelse, som er skjæringspunktet mellom aksene.

-De Kvadranter, som er regionene som koordinataksene bestemmer på flyet og telles i motsatt retning av klokkehendene, og starter med den første kvadranten. De er definert som følger:

• Første kvadrant: akser x og og positivt.
• Andre kvadrant: tilsvarer den negative x -aksen og og positiv akse.
• Tredje kvadrant: Den har begge negative akser.
• Fjerde kvadrant: med den positive x -aksen og og negativ aksen.

Generelt er kvadranter betegnet i romertall, som dette:

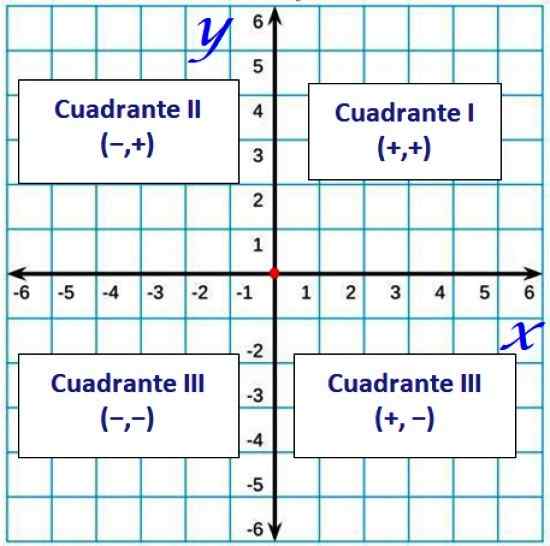Figur 2. Cuadrants i det kartesiske flyet. Kilde: f. Zapata.

Bestilte par og avstand mellom to punkter

De bestilte parene er koordinatene for hvert punkt, der X -koordinaten alltid er plassert først, som i eksemplet på figur 1. Koordinater (3,4) av punkt P indikerer at x = 3 og y = 4.

I denne andre figuren nedenfor tilhører punkt P IV -kvadranten og har koordinater (2; −1.5). Merk at ved å projisere linjer fra koordinataksene til punktet d danner et rektangel. Dette er grunnen til at kartesiske koordinater også blir kalt Rektangulære koordinater.

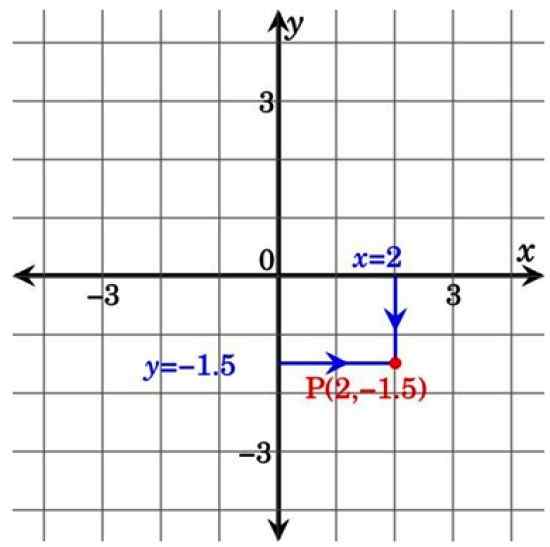Figur 3. Pek på det kartesiske flyet. Kilde: Wikimedia Commons.

Kartesiske planapplikasjoner

Det kartesiske flyet har mange applikasjoner på mange felt. Opprinnelig introduserte Descartes det for grafkurver av kurver i flyet, og det er derfor det regnes som faren til analytisk geometri.

Kan tjene deg: Cruz -produkt

Imidlertid strekker bruken seg til å tegne alle slags forhold og funksjoner, for eksempel:

-Følg banen til et legeme med parabolsk, sirkulær eller krumlinjet bevegelse generelt.

-Bestem grafisk måten to variabler er relatert gjennom en funksjon.

-Finn punkter på flatt land for å lette målinger på dem.

Referanser

1. Matematikk er morsomt. Kartesiske koordinater. Gjenopprettet fra: matematikk.com/data/cartesian-koordinater.
2. Det kartesiske flyet. Hentet fra: DL.UNCW.Edu.