Befolkning og prøve

De forskjeller mellom populasjon og prøve I statistikk stammer de fra det faktum at befolkningen er universet av elementer å studere, mens utvalget er en representativ del av befolkningen.

Analysere en prøve hentet fra settet, i stedet for hele. La oss se nedenfor mer detaljert hovedforskjellene mellom begge konseptene.

Det er nå klart at en populasjon kan bestå av et veldig stort sett med elementer: mennesker, dyr, mikroorganismer eller partikler. Å adressere studiet av hvert av disse elementene bruker separat mange ressurser, tid og krefter.

Men når du velger en nøye valgt prøve, strekker resultatene fra studien seg til befolkningen, uten vesentlige tap av informasjon.

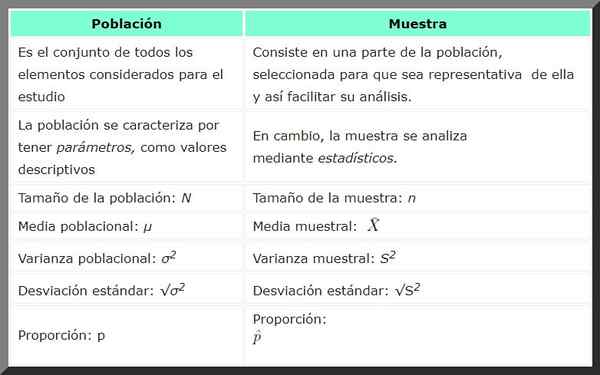
	Befolkning	Prøve
Definisjon	Settet med alle elementene som vurderes for en studie.	Det er en del av befolkningen, valgt til å være representativ og dermed lette analysen.
Symbol	Befolkningsstørrelse: n	Prøvestørrelse: n
Analyse	Har parametere, som beskrivende verdier.	Det analyseres ved statistikk.
Eksempler	Totalt antall fugler som bor i en skog.	For undersøkelse er 1000 fugler hentet fra en skog.

Hva er en befolkning?

Befolkningen er det totale antallet mennesker som bor i et sted, det være seg en by, en by, en stat eller et land. Utvalget er en del av den befolkningen

I statistikk har befolkningsbegrepet en bredere betydning enn det daglige. En befolkning er assosiert med antall innbyggere i et land eller en by, men en statistisk befolkning kan bestå av levende mennesker og vesener, men også store og små gjenstander, partikler, hendelser, hendelser og ideer.

Kan tjene deg: Fourier Transform: Egenskaper, applikasjoner, eksempler

Eksempler på populasjoner av mangfoldig natur er:

-Luftmolekyler inne i en forseglet beholder.

-Alle stjernene på Melkeveien.

-Fuglene som befolker en skog.

Et eksempel på en befolkning som studerer ornitologer: fuglene i en skog

-Det totale antallet trær av den samme eller annen skog.

-Abonnentsettet til et telefonselskap som har filialer i Amerika og Europa.

-Utgivelsene vi lager av en mynt.

-Antall bakterier i en avling.

-Månedlig skrueproduksjon på en fabrikk.

Befolkningskarakteristikker

Vi vet allerede hvor forskjellige befolkninger kan være. La oss nå se hvordan de kan klassifiseres i henhold til utvidelsen.

En begrenset mengde er en som kan uttrykkes av en figur, for eksempel mengden klinkekuler i en boks. På den annen side, av en uendelig mengde, kan vi ikke gi en presis verdi.

Denne forskjellen vil tillate oss å definere to typer populasjoner i henhold til utvidelsen.

Endelige befolkninger

Anta at det er 20 klinkekuler i en boks og prøver av 2 kuler blir trukket ut uten erstatning. Etter hvert vil kulene til boksen være utmattet, derfor er befolkningen begrenset.

Et tall kan være begrenset selv om det er veldig stort. En bakteriekultur består av et stort antall, men den er begrenset, og det samme er mengden stjerner i galaksen eller molekylene til en gassdel låst i en beholder.

Uendelige populasjoner

Hva skjer hvis vi hver gang vi henter ut en marmorprøve, returnerer vi dem til boksen etter å ha observert dem? I så fall kan vi få et uendelig antall prøver, og dermed vurdere at marmorpopulasjonen er uendelig.

Kan tjene deg: sekskantet prisme

Et annet eksempel på den uendelige befolkningen er ved lanseringen av mynter eller terninger, siden du i teorien kan ta alle de ønskede prøvene, uten noen grense.

Selv en endelig befolkning som er kjent inneholder mange elementer, kan den betraktes som uendelig i praksis, om nødvendig.

Det er grunnen til.

Andre viktige egenskaper

Det er også viktig å kjenne den kronologiske plasseringen av befolkningen. Det er ikke det samme å studere registreringer av innbyggerne i en stor by på begynnelsen av 1900 -tallet enn å gjøre det samme med innbyggerne i samme by på begynnelsen av det 21. århundre.

Analytikeren må også ta seg av å ta hensyn til befolkningenes beliggenhet, i tillegg til å finne ut deres homogenitet -eller mangel på den-.

Hva er et utvalg?

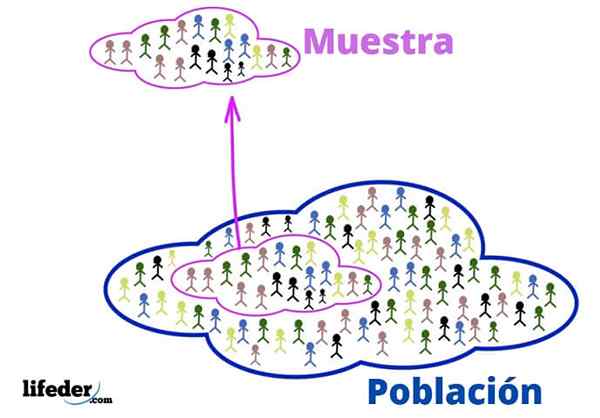Befolkning og prøve

Utvalget er settet med utvalgte elementer blant befolkningen for å representere det. Målet med å gjøre dette, som vi sa, er å lette arbeidet. Når du håndterer mindre data, blir mindre mengder ressurser reversert og raskere resultater oppnås.

For at dens funksjon skal oppfylle, må prøven imidlertid være tilstrekkelig. Utvelgelsesprosessen utføres gjennom prøvetakingsteknikker som bruker matematiske kriterier.

Den ekstraherte prøven trenger ikke å være unik. Faktisk kan en befolkning føre til forskjellige prøver.

Det kan tjene deg: trigonometriske grunner: eksempler, øvelser og applikasjoner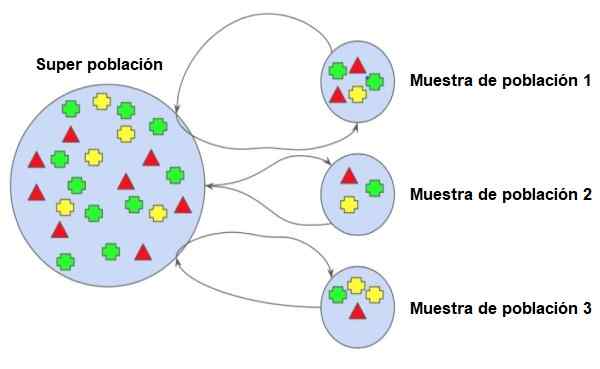 Ulike prøver hentet fra en befolkning. Kilde: Wikimedia Commons.

Anta for eksempel at befolkningen er settet med studenter i et videregående utdanningssenter som har flere seksjoner for hver karakter. Et representativt utvalg skal inneholde noen studenter fra hver av seksjonene i hver grad, for eksempel de hvis navn begynner med brev a.

På den annen side kan en ikke så representativ prøve være hvis alle studenter i samme grad ble valgt. La oss se på noen flere eksempler:

Eksempel 1

Eierne av varehusene ønsker å estimere det gjennomsnittlige beløpet som kundene bruker. For å gjøre dette samler de alle fakturaene fra en viss periode, sier ett år.

Mengden fakturaer fra det siste året er befolkningen å analysere.

Nå, hvis denne gruppen er trukket ut et helt tilfeldig utvalg på 150 fakturaer, ville det allerede være prøven.

Eksempel 2

Når valget nærmer seg, enten nasjonale eller lokale, ansetter politiske partier vanligvis spesialiserte selskaper for dataanalyse. På denne måten vet de intensjonen om innbyggernes avstemning og planlegger passende kampanjestrategier.

I dette tilfellet består befolkningen av hele universet av velgere som er registrert i det tilsvarende valgsystemet.

Siden det vil ta mye tid og krefter å lokalisere og avhøre hver velger, velger Pollsters et utvalg av velgere å kartlegge og derfra trekker ut prosentene og bestemmer trendene.

Utvalget av passende utvalg er bare begynnelsen, men det er et avgjørende trinn for å sikre suksessen til studien.

Referanser

1. Berenson, m. 1985. Statistikk for administrasjon og økonomi, konsepter og applikasjoner. Inter -amerikansk redaksjon.
2. Brase/Brase. 2009. Undervurderbar statistikk. 9. Utgave. Hougton Mifflin.
3. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørfag og vitenskap. 8. Utgave. Cengage Learning.
4. Galindo, e. 2011. Statistikk, metoder og applikasjoner. Redaktører Procriation.
5. Levin, r. 1981. Statistikk for administratorer. Prentice Hall.
6. Matemobile. Befolkning og prøve, eksempler og øvelser. Gjenopprettet fra: Matemovil.com.