Konveks polygondefinisjon, elementer, egenskaper, eksempler

EN Konveks polygon Det er en geometrisk figur inneholdt i et plan som er karakterisert fordi det har alle diagonalene inni og dets vinkler måler mindre enn 180º. Blant dens egenskaper er følgende:

1) Den består av n påfølgende segmenter der det siste av segmentene blir med den første. 2) Ingen av segmentene krysses på en slik måte som avgrenser flyet i et interiør og et annet ytre. 3) Hver eneste av vinklene i det indre området er strengt lavere enn en flat vinkel.

Figur 1. Polygoner 1, 2 og 6 er konvekse. (Utarbeidet av Ricardo Pérez).

En enkel måte å avgjøre om en polygon er konveks eller ikke skal vurdere linjen som går gjennom en av sidene, som bestemmer to semplaner. Hvis på hver linje som passerer på den ene siden, er de andre sidene av polygonen i samme semplan, er det da en konveks polygon.

[TOC]

Elementer av en polygon

Hver polygon består av følgende elementer:

- Sider

- Hjørner

Sidene er hvert av de påfølgende segmentene som utgjør polygonen. I en polygon kan ingen av segmentene som utgjør det ha en åpen ende, i så fall ville det være en polygonal linje, men ikke en polygon.

Hjørnene er unionspunktene til to påfølgende segmenter. I en polygon tilsvarer antall hjørner alltid antall sider.

Hvis to sider eller segmenter av et polygonkors, har du et krysspolygon. Kryssingspunktet regnes ikke som et toppunkt. A Cross Polygon er en ikke-konveks polygon. De krasjede polygonene er kryssede polygoner og er derfor ikke konvekse.

Det kan tjene deg: analytisk geometri

Når en polygon har alle sidene av samme lengde, er det da en vanlig polygon. Alle vanlige polygoner er konvekse. 

Konvekse og ikke-konvekse polygoner

Figur 1 viser flere polygoner, noen av dem er konvekse og andre er det ikke. La oss analysere dem:

Nummer 1 er en tre -sidig polygon (trekant) og alle indre vinkler er mindre enn 180º, derfor er det en konveks polygon. Alle trekanter er konvekse polygoner.

Tallet 2 er en firesidig polygon (firkantet) der ingen av sidene blir oppfanget og også hver eneste av de indre vinklene er mindre enn 180º. Det er da en fire -sidig konveks polygon (konveks kvadrilateral).

På den annen side er nummer 3 en firesidig polygon, men en av de indre vinklene er større enn 180º, så den oppfyller ikke konveksitetstilstanden. Det vil si at det er en ikke-konveks-sidig polygon som kalles en konkav firedoblet.

Tallet 4 er en firesegment (sider) polygon, hvorav to er avskjæret. De fire indre vinklene er mindre enn 180 º, men ettersom to sider krysser de er de et ikke-konveks kryss-polygon (Cross Quadrilateral).

En annen sak er nummer 5. Dette er en fem -sidig polygon, men ettersom en av de indre vinklene er større enn 180º, er det da en konkav polygon.

Til slutt har tallet 6, som også har fem sider, alle sine indre vinkler mindre enn 180 º, så det er en fem -sidig konveks polygon (konveks Pentagon).

Kan tjene deg: Prøvetakingsfeil: Formler og ligninger, beregning, eksempler

Konvekse polygonegenskaper

1- En ikke-knust polygon eller enkel polygon deler flyet som inneholder det i to regioner. Interiørregionen og det ytre regionen, og er polygon grensen mellom de to regionene.

Men hvis polygonen i tillegg er konveks, så er det en indre region som ganske enkelt er relatert, noe som betyr at det å ta to punkter i indre region, alltid kan forenes av et segment som hører i sin helhet til det indre regionen.

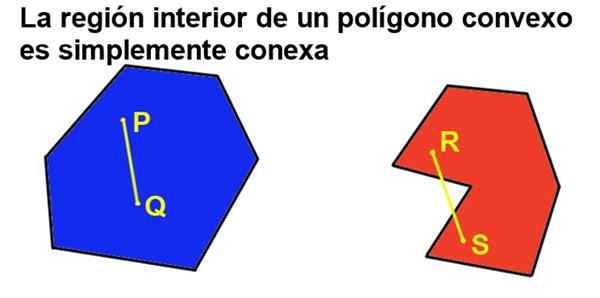Figur 2. En konveks polygon er ganske enkelt relatert, mens en konkav ikke er det. (Utarbeidet av Ricardo Pérez).

2- All indre vinkel på en konveks polygon er mindre enn en flat vinkel (180 º).

3- Alle interiørpunktene til en konveks polygon tilhører alltid en av de halvdefinerte av linjen som passerer gjennom to påfølgende vertikaler.

4- I en konveks polygon er alle diagonaler fullt inne i det indre polygonregionen.

5- Interiørpunktene til en konveks polygon hører i sin helhet til den konvekse vinkelsektoren definert av hver indre vinkel.

6- Hver polygon der alle sine hjørner er på en omkrets er en konveks polygon som kalles syklisk polygon.

7- Hver syklisk polygon er konveks, men ikke hver konveks polygon er syklisk.

8- Hvert ikke-knust polygon (enkel polygon) som har alle sidene av samme lengde er konveks og er kjent som vanlig polygon.

Diagonaler og vinkler i konvekse polygoner

9- Det totale antall diagonaler av en konveks polygon av N-sider er gitt av følgende formel:

Det kan tjene deg: polybal grafikk

N = ½ n (n - 3)

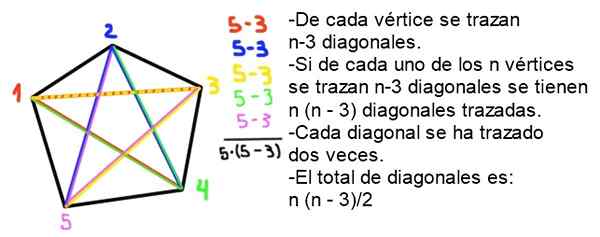
Demonstrasjon: I en konveks polygon av N -sider av hvert toppunkt trekkes n - 3 diagonaler, siden selve toppunktet og de to tilstøtende er ekskludert. Ettersom det er N -hjørner, trekkes de i total n - 2) diagonaler, men hver diagonal ble tegnet to ganger, så antall diagonaler (uten repetisjon) er n (n -2)/2.

10- Summen av de indre vinklene til en konveks polygon av N-sider er gitt av følgende forhold:

S = (n - 2) 180º

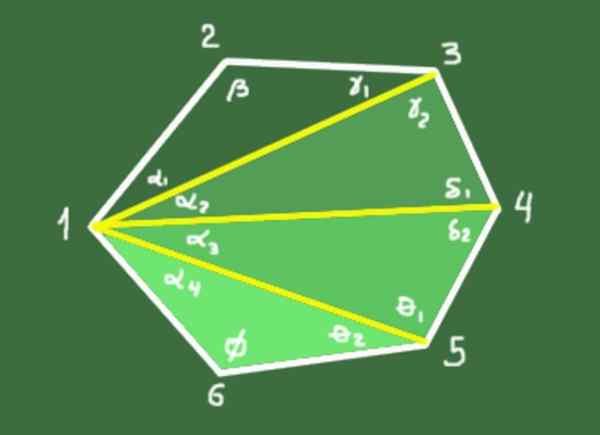
Demonstrasjon: N-3-diagonaler er trukket fra et toppunkt som definerer N-2-trekanter. Summen av de indre vinklene til hver trekant er 180º. Den totale summen av N-2-trekantenvinkene er (n-2)*180º, som sammenfaller med summen av de interne vinklene til polygon.

Eksempler

Eksempel 1

Syklisk sekskant, det er en seks -sidig polygon og seks hjørner, men alle hjørner er i samme omkrets. All syklisk polygon er konveks.

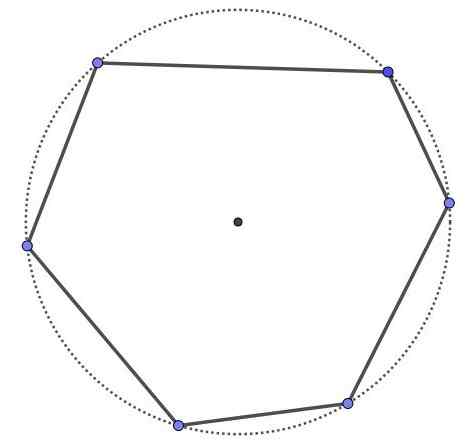Syklisk sekskant.

Eksempel 2

Bestem verdien av de indre vinklene til en vanlig enegon.

Løsning: Enegon er en 9 -sidig polygon, men den regulerer også alle sider og vinkler er de samme.

Summen av alle indre vinkler til en 9 -sidig polygon er:

S = (9 - 2) 180º = 7 * 180º = 1260º 

Men det er 9 interne vinkler med like mål α, så følgende likhet må oppfylles:

S = 9 α = 1260º

Fra hvor det følger at α -målet for hver indre vinkel på den vanlige enegon er:

α = 1260º/9 = 140º