Vanlige polygonsegenskaper, elementer, vinkler, eksempler

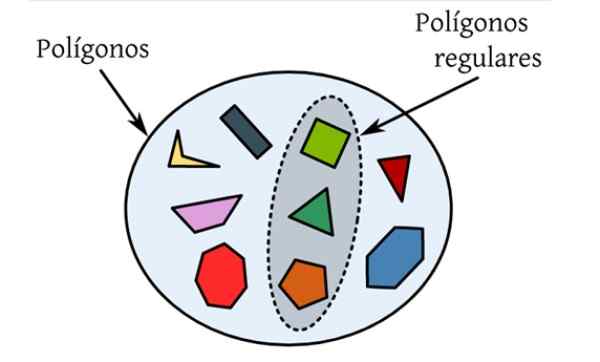
De Vanlige polygoner De er de som har alle sidene og deres like interne vinkler. I den følgende figuren er det et sett med forskjellige polygoner, som er flate figurer begrenset av en lukket kurve, og bare de som blir fremhevet oppfyller forholdene for å være vanlige.

For eksempel er den likeverdige trekanten en vanlig polygon, siden dens tre sider måler det samme, så vel som dens indre vinkler, som er verdt 60 º hver.

Figur 1. Vanlige polygoner er de hvis sider og indre vinkler er de samme, for eksempel den liksidige trekanten og firkanten. Kilde: Wikimedia Commons.

Torget er en firkantet med fire sider med like mål og hvis indre vinkler er 90º. Det blir fulgt av den vanlige Pentagon, med fem sider av like størrelse og fem indre vinkler på 108º hver.

Når en polygon er regelmessig, blir dette ordet lagt til sitt spesielle navn, og dermed har vi den vanlige sekskanten, den vanlige heptagon og så videre.

[TOC]

Egenskaper til vanlige polygoner

De viktigste egenskapene til vanlige polygoner kan oppsummeres som følger:

-Sidene måler det samme, derfor er de likeverdige.

-Er Equiagular, Vel, alle dens indre vinkler har like store mål.

-De kan alltid registrere seg i en omkrets, noe som betyr at de passer perfekt inn i en, som kalles Omskrevet omkrets.

-For en vanlig polygon av N -sider er målet på en indre vinkel α:

α = [180 (n-2)]/n

-N-3)/2 diagonaler kan trekkes fra toppunktene til en polygon, enten det er regelmessig eller ikke.

-Summen av utvendige vinkler Det er lik 360º.

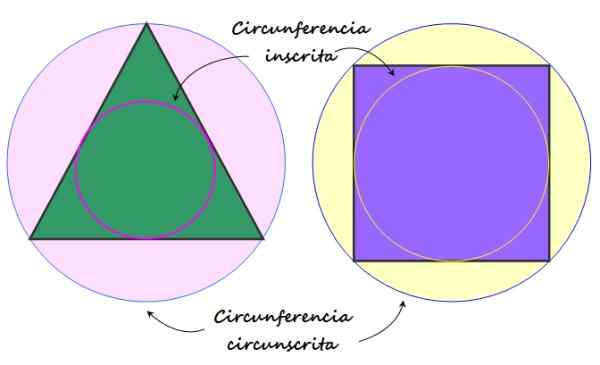Figur 2. Registrert omkrets og omkrets omskrevet til vanlig polygon. Kilde: f. Zapata.

Elementer av en vanlig polygon

Så presenterer vi hovedelementene i en vanlig polygon, visualisert i det nedre figuret.

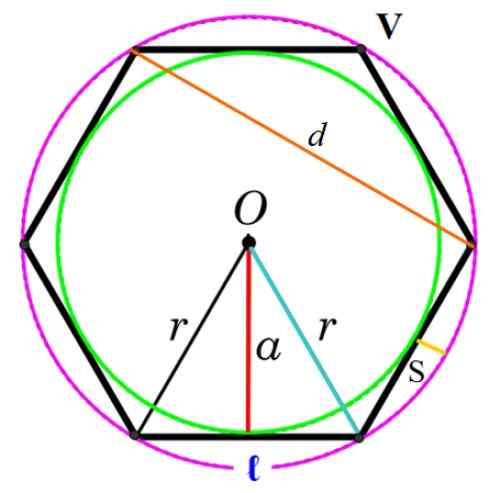Figur 3. Elementer i den vanlige polygonen. Kilde: f. Zapata.

Toppunkt

Felles punkt som har to påfølgende sider, betegnet som V i figuren.

Side

Det er segmentet som blir med to påfølgende vertikater av polygon og er betegnet som ℓ eller l.

Diagonal

Segment som blir sammen med to ikke -sammenhengende toppunkter av polygon, i figuren er det betegnet som d.

Senter

Det er det vanlige sentrum av den registrerte omkretsen og den omskrevne omkretsen, betegnet med brevet eller. Det kan også sees på som det eneste punktet som ekvidista av både toppunktene og midtpunktene på hver side.

Radio

Det er radioen r av den omskrevne omkretsen og sammenfaller med avstanden mellom O og et toppunkt.

Det kan tjene deg: aksiomer av sannsynlighet: typer, forklaring, eksempler, øvelser

Apothem

Det kalles Apothem til omkretsens radius innskrevet i polygonen, representert i figuren med en bokstav til. Apothemet er vinkelrett på siden og forener dette med sentrum O (rødt segment i figur 3).

Når du kjenner radius r og lengden på siden, beregnes apothemet av:

Siden Apothem faktisk er en av kategoriene i et rektangel -trekant (se figur 3), den andre katetoen er verdien av ℓ/2 (halvparten av den ene siden) og hypotenuse radioen r av polygonen.

Når Pythagoras -teoremet blir brukt til nevnte trekant, oppnås denne ligningen, som er gyldig ikke bare for sekskant, men for enhver vanlig polygon.

Sentral vinkel

Det er vinkelen hvis toppunkt sammenfaller med sentrum eller hvis sider er segmentene som forener sentrum med to påfølgende vertikaler. Dets mål i sexagesimale grader er 360º/n, hvor n Det er antall sider av polygonen.

Sagita

Det er forskjellen mellom polygonens radius og Apothem (se figur 3). Betegner Sagita som s:

S = r - a

Omkrets og område

Omkrets

Det beregnes enkelt ved å legge til lengdene på sidene. Ettersom hvilken som helst side er samme lengde l og det er n sider, uttrykkes omkretsen P som:

P = n.L

Område

I en vanlig polygon er området A gitt av produktet mellom semi-perimeteret (halvparten av omkretsen) og apotemelengden til.

A = s.A /2

Siden omkretsen avhenger av antall sider n, viser det seg at:

A = (nl).A /2

To vanlige polygoner kan ha samme omkrets selv om de ikke har samme antall sider, siden det da vil avhenge av lengden på sidene.

I bok V av din Samling, Matematikeren Pappus of Alexandria (290-350), den siste av de store greske matematikerne av antikken, viste at blant alle vanlige polygoner med samme omkrets, er den med det største området den med størst antall sider.

Vinkler

Figur 4 viser de relevante vinklene i en vanlig polygon, betegnet med de greske bokstavene α, β og y.

Sentral vinkel

Tidligere nevner vi den sentrale vinkelen, blant elementene i den vanlige polygon, er det vinkelen hvis toppunkt er i sentrum av polygonen og sidene er segmentene som forener sentrum med to påfølgende vertikaler.

For å beregne målet på den sentrale vinkelen α, 360º er delt med n, antall sider. Eller 2π radianer mellom n:

Kan tjene deg: Injeksjonsfunksjon: Hva den består av, hva er det for og eksempler

α = 360º/n

Tilsvarende i radianer til:

α = 2π /n

Indre vinkel eller indre vinkel

I figur 4 er den indre vinkelen β den hvis toppunkt sammenfaller med en av figuren og sidene er sider av figuren også. Det beregnes i sexagesimale grader av:

β = [180 (n-2)]/n

Eller i radianer som bruker:

β = [π (n-2)]/n

Eksterne vinkler

De er betegnet med den greske bokstaven y. I figuren observeres det at γ + β = 180º. Derfor:

γ = 180º - β

Summen av alle ytre vinkler til en vanlig polygon er 360º.

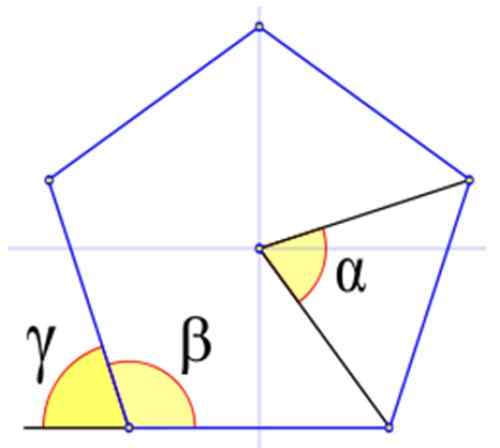Figur 4. Vinklene i en vanlig polygon, i dette eksemplet en vanlig Pentagon. Kilde: Wikimedia Commons.

Eksempler på vanlige polygoner

Nedenfor har vi de første 8 vanlige polygonene. Vi observerer at når antall sider øker, blir polygonen mer og mer til omkretsen de er registrert.

Vi kan forestille oss at å gjøre lengden på sidene stadig liten, og øke antallet av disse, vi får omkretsen.

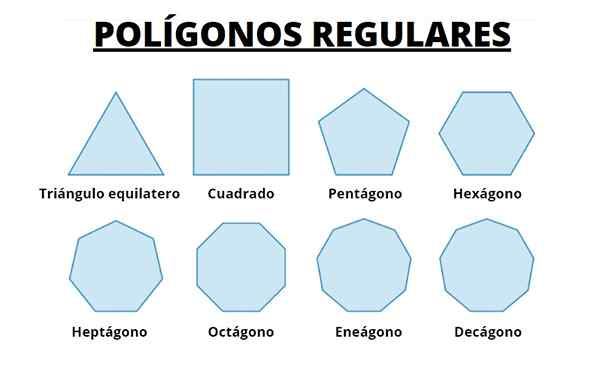Figur 5. De åtte første vanlige polygonene. Kilde: Wikimedia Commons.

- Vanlige polygoner i dagliglivet og naturen

Vanlige polygoner finnes overalt i dagliglivet og til og med i naturen. La oss se på noen eksempler:

Trafikklys

I skiltingen ser vi på motorveier og veier florerer vanlige polygoner som likeverdige, firkantede og rhomb -trekanter. I figur 6 ser vi et høyt formet signalsignal.

Figur 5.- Trafikksignal med åttekantet form. Kilde: Pixabay.

Møbler

Utallige møbelstykker er for eksempel firkantet, som en karakteristisk geometrisk figur, så vel som mange bord, stoler og banker er firkantede. En parallellpiped er vanligvis en boks med rektangel -formede sider (som ikke er en vanlig polygon), men de kan også lage firkant.

Arkitektur og konstruksjon

Flisene eller flisene på gulv og vegger, både i hjem og i gatene, har ofte form av vanlige polygoner.

Teselene er overflater dekket helt med fliser som har forskjellige geometriske figurer. Med trekanten kan kvadratet og sekskanten gjøres vanlige tesselver, de som bare bruker en enkelt type figur til å belegge perfekt, uten tomme mellomrom (se figur 6).

Også bygningene benytter seg av vanlige polygoner i elementer som vinduer og dekorasjon.

Figur 6. Firkantet fliser. Kilde: Pixabay.

- Vanlige sekskanter i naturen

Overraskende nok er vanlig sekskant en polygon som ofte vises i naturen.

Kan tjene deg: diskrete distribusjoner

Honningkaker laget av bier for å lagre honning har en veldig omtrentlig form til en vanlig sekskant. Som Pappus of Alexandria observerte, optimaliserer bier bier for å spare så mye honning som mulig som mulig.

Og det er også vanlige sekskanter i skallet av skilpadder og snøfnugg, som også tar i bruk forskjellige veldig vakre geometriske former.

Trening løst

En vanlig sekskant er en del av en halvsirkel på 6 cm radius, som vist på figuren. Hva er verdien av det skyggelagte området?

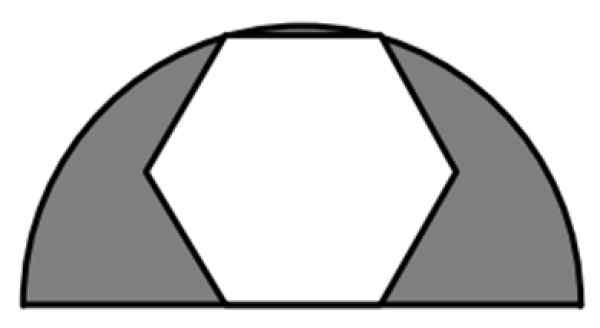Figur 7. En vanlig sekskant registrert i en halvsirkel. Kilde: f. Zapata.

Løsning

Det skyggelagte området er forskjellen mellom radius halvcirkelområdet r = 6 cm og hele sekskantområdet, en vanlig 6 -sidig polygon. Så vi trenger formler for området for hver av disse figurene.

Halvsirkelområde

TIL₁ = π r² /2 = π (6 cm)² /2 = 18π cm²

Vanlig sekskantområde

Formelen for beregning av området til en vanlig polygon er:

A = s.A /2

Hvor P Det er omkretsen og til Det er apothem. Siden omkretsen er summen av sidene, trenger vi verdien av disse. For vanlig sekskant:

P = 6ℓ

Derfor:

A = 6ℓa /2

For å finne verdien av siden ℓ er det nødvendig å bygge hjelpestall, som vi vil forklare nedenfor:

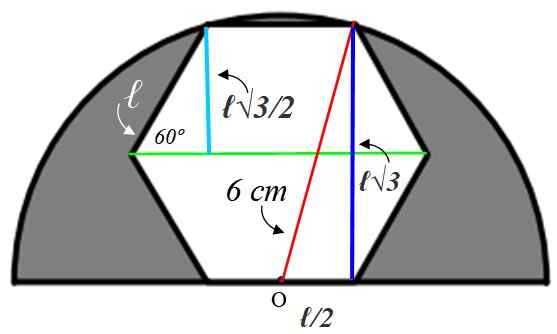
La oss starte med den lille rektangeletrekanten til venstre, hvis hypotenuse er ℓ. En intern vinkel på sekskanten er verdt:

α = [180 (n-2)]/n = α = [180 (6-2)]/6 = 120º

Radius som vi har trukket i bisekta grønn denne vinkelen, derfor er den akutte vinkelen på den lille trekanten 60º. Med informasjonen som er gitt, løses denne trekanten, og finner den lyseblå siden, som måler det samme som apothem:

Motsatt kateto = a = ℓ x sin 60º = ℓ √3 / 2 cm

Denne verdien er det dobbelte av den mørkeblå benet på den store trekanten til høyre, men fra den trekanten vet vi at hypotenusen måler 6 cm fordi det er radius i halvsirkelen. Den gjenværende kateto (nedenfor) er verdt ℓ/2 siden punktet eller er midt på siden.

Siden indre vinkler på denne trekanten ikke er kjent, kan vi heve Pythagoras -teoremet for ham:

36 = 3 ℓ² + ℓ² / 4

(13/4) ℓ² = 36 → ℓ = √ (4 x36) /13 cm = 12 /√13 cm

Med denne verdien beregnes apothemet:

a = ℓ ℓ3 /2 cm = (12 /√13) x (√3 /2) cm = 6√3 /√13 cm

La oss ringe a₂ Til det vanlige sekskantområdet:

= 28. 8 cm²

Skyggelagt figurområde

TIL₁ - TIL₂ = 18π cm²  - 28.8 cm² = 27.7 cm²

Referanser

1. Baldor, a. 1973. Geometri og trigonometri. Sentralamerikansk kulturell redaksjon.
2. Kos deg med matematikk. Tesels. Gjenopprettet fra: Nytmatimaticas.com.
3. OG. TIL. 2003. Geometrielementer: med øvelser og kompassgeometri. University of Medellin.
4. Heksagoner i naturen. Gjenopprettet fra: Malvargamath.WordPress.com.
5. Jiménez, r. 2010. Matematikk II. Geometri og trigonometri. Andre utgave. Prentice Hall.
6. Vanlige polygoner. Gjenopprettet fra: kompis.Ingeniørfag.USAC.Edu.Gt.
7. Wikipedia. Apothem. Gjenopprettet fra: er.Wikipedia.org.