Hydrostatisk trykkformel, beregning, eksempler, øvelser

De Hydrostatisk trykk Det er den som utøver en væske i statisk likevekt hvor som helst inne, enten et område nedsenket i den, veggene i beholderen eller en del av væsken som er en del av den totale massen.

Måten væsker utøver trykk fra faste stoffer. Disse utøver nedtrykk, men en væske eller en gass gjør det i alle retninger.

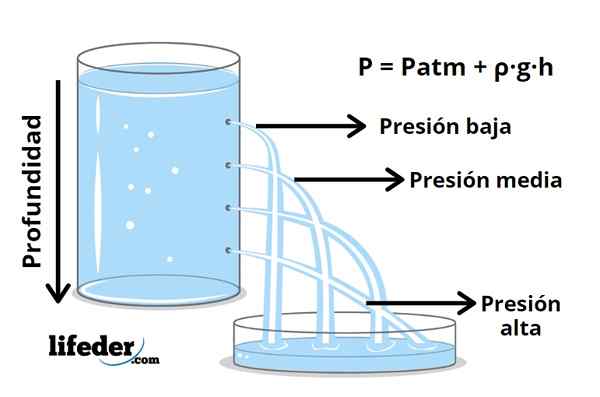
Figur 1- med større dybde større trykk

Når det gjelder en væske, øker trykket med dybden, som kjent av erfaring når du senker deg i vannet der økningen i trykket merkes i ørene. Dette trykket kommer fra væskens vekt og den ustanselige bevegelsen av partiklene som komponerer den, som kontinuerlig treffer overflaten av kroppen nedsenket i væsken.

Hvis vi antar en inkomprimerbar væske - som er sant i de aller fleste anvendelser, - dens tetthet forblir konstant og i så fall avhenger trykket lineært på dybden.

[TOC]

Formel

Hydrostatisk trykk beregnes ved følgende uttrykk:

P = p_ATM + ρ · g · h

Hvor:

-P trykket utøvd på et punkt

-P_ATM Det er trykket fra atmosfæren på den frie overflaten

-ρ er væsketetthet

-G er akselerasjonen av tyngdekraften

-H er dybden du vil beregne det hydrostatiske trykket 

Formelen inkluderer effekten av atmosfæren, men mange trykk eller manometre plasserer 0 i atmosfæretrykk, av denne grunn er det de måler differensialtrykk eller relativt trykk, også kalt kalt måle trykk:

P_m = ρ · g · h

Når det gjelder gasser, blir de komprimert eller utvidet veldig enkelt. Derfor er tettheten, som er årsaken mellom masse og volum, vanligvis en funksjon av andre parametere, for eksempel høyde og temperatur, i tilfelle av atmosfæriske gasser.

Det kan tjene deg: magnetisering: orbital og spinn magnetisk øyeblikk, eksempler

Trykket som gassene utøver kalles vanligvis Aerostatisk trykk, begrepet hydrostatisk trykk for at væsker blir reservert.

Hydrostatiske trykkeksempler

Hydrostatisk trykk avhenger bare av dybden, så formen eller arealet på basen til beholderen er ikke relevant.

Siden P -trykket er definert som den vinkelrett komponenten i kraften F per enhet av område A:

P = f/a

Da kan kraften utøvd av væsken i bunnen av en beholder være annerledes, men å bli distribuert over forskjellige utvidelser, er trykket, som er kraft/områdeforholdet, det samme for poeng til samme dybde.

Tenk på containerne på figuren. Trykket er det samme for alle de røde punktene som er på samme nivå, selv om det er en større mengde væske over det nivået i den sentrale beholderen -mer bredde -hvorav det er det sylindriske og tynne røret på det ekstreme venstre.

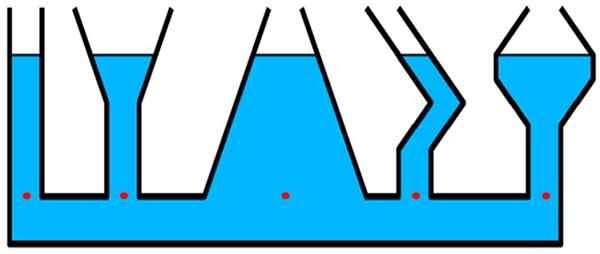Figur 2.- Trykket ved noen av de røde punktene er det samme, uavhengig av formen på beholderen. Kilde: Wikimedia Commons.

Strukturer der hydrostatisk trykk er relevant

-Veggene i en demning: Selv om kraften er den samme for alle punktene på den flate bunnen, på den vertikale veggen vokser den når dybden øker, så støttemurene er bredere i basen enn i den øvre delen.

-På veggene og bunnen av et basseng.

-I stjerner som vår sol, der hydrostatisk trykk balanserer tyngdekraften og holder stjernen i drift. Når nevnte balanse er ødelagt, kollapser stjernen og lider ekstreme endringer i strukturen.

Kan tjene deg: Hva er det magnetiske øyeblikket?

-Flytende lagringstanker, designet for å motstå hydrostatisk trykk. Ikke bare veggene, men portene som letter fylling og ekstraksjon. For utformingen blir det tatt i betraktning hvis væsken er etsende og også trykket og kraften den utøver i henhold til dens tetthet.

-Dekk og ballonger, som er infisert på en slik måte at de motstår væsketrykk (gass eller væske) uten å rive.

-Enhver nedsenket kropp, som opplever en vertikal skyvekraft, eller "lettelse" av vekten, takket være det hydrostatiske trykket som væsken utøver. Dette er kjent som Archimedes 'prinsipp.

Øvelser

Archimedes -prinsippet bekrefter at ved å senke et legeme, totalt eller delvis, vil det oppleve en vertikal kraft oppover, kjent som skyvekraft. Størrelsen på skyvekraften er numerisk lik vekten av volumet av vann som er fortrengt av objektet.

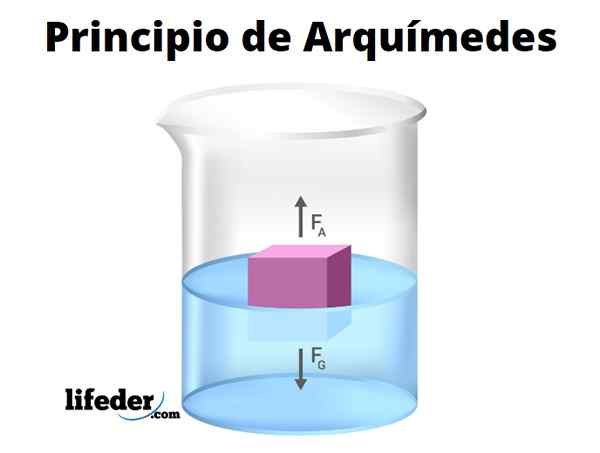
Være ρ_flytende Væsketettheten, V_s Det nedsenkede volumet, g akselerasjonen av tyngdekraften og b størrelsen på skyvekraften, som vi kan beregne med følgende uttrykk:

B = ρ_flytende .V_s .g

- Oppgave 1

En rektangulær blokk hvis dimensjoner er 2.0 cm x 2.0 cm x 6.0 cm flyter i ferskvann med sin lengste vertikale akse. Lengden på blokken som skiller seg ut over vannet er 2.0 cm. Beregn blokkeringstetthet.

Løsning

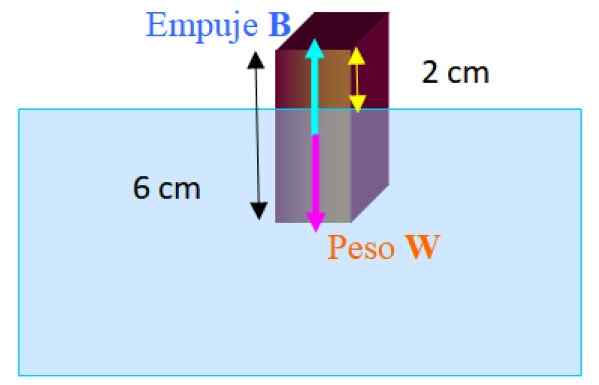Figur 3.- Gratis kroppsdiagram for blokken som flyter delvis nedsenket i vann. Kilde: f. Zapata.

Kreftene som virker på blokken er vekten W ned og skyv B oppover. Når blokken flyter i likevekt du har:

∑ f_og = B - W = 0

B = w

Vektets størrelse w er produktet av masse m av blokken på grunn av tyngdekraften akselerasjon. Vi vil bruke definisjonen av tetthet ρ_enten Som kvotienten mellom massen m og volumet V av blokken:

Kan tjene deg: Meshealanalyse: konsepter, metoder, eksempler

ρ_enten = m / v → m = ρ_enten . V

For sin del er skyvekraften:

B = ρ_flytende .V_s .g

Utjevningsstørrelse på skyvekraften og størrelsen på vekten:

ρ_flytende .V_s .G = ρ_enten . V.g

Tyngdekraften kanselleres for å være som en faktor på begge sider, og tettheten av blokken kan tømmes som:

ρ_enten = ρ_flytende . (V_s  / V)

Vanntetthet i internasjonale systemenheter er 1000 kg/m³. Totalt v -volum og nedsenket V_s, De beregnes med V = bredde x høy x dybde:

V = 2.0 cm x 2.0 cm x 6.0 cm = 24.0 cm³

V_s = 2.0 cm x 2.0 cm x 4.0 cm = 16.0 cm³

Erstatte verdier:

ρ_enten = ρ_flytende . (V_s  / V) = 1000 kg/ m³ . (16/24) = 667 kg/m³

- Oppgave 2

Beregn den nedsenkede volumprosenten av et isstykke som flyter i sjøvann til 0 ºC.

Løsning

Ice flyter i vann, siden dens tetthet er lavere: 916.8 kg/m³, Noe som betyr at det utvides når det avkjøles, i motsetning til de fleste stoffer, at når de varmer opp, øker de volumet.

Figur 4. Nesten hele et isfjells volum forblir nedsenket. Kilde: Pixabay.

Det er en veldig heldig omstendighet for livet, siden da fryser massene bare på overflaten, og forblir væske i dybden.

Tettheten av sjøvann er litt større enn for ferskvann: 1027 kg/m³. Vi beregner volumfraksjonen V_s  / V:

V_s  / V = ​​ρ_enten / ρ_flytende = 916.8 kg/m³  / 1027 kg/ m³ = 0.8927

Dette betyr at omtrent 89 % av isen forblir nedsenket under vann. Bare 11 % er synlig flytende på sjøen.

Referanser

1. Giambattista, a. 2010. Fysikk. 2. Ed. McGraw Hill.
2. Knight, r.  2017. Fysikk for forskere og ingeniørfag: En strategitilnærming. Pearson.
3. Cimbala, ca. 2006. Mekanikk av væsker, grunnleggende og applikasjoner. MC. Graw Hill.
4. Hibbeler, R. 2015. Væskemekanikk. 1. Ed. Pearson.
5. Mott, r.  2006. Væskemekanikk. 4. plass. Utgave. Pearson Education.
6. Streeter, v. 1999. Væskemekanikk. McGraw Hill.