Hva er delene av brøkdelen? (Eksempler)
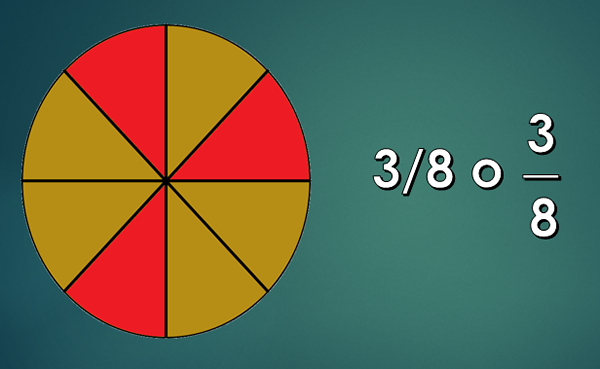
- 3671
- 940
- Jonathan Carlsen
De deler av brøkdelen De er delt inn i tre som er: deres teller, en horisontal eller diagonal bar og denominatoren. Derfor, hvis du vil betegne brøkdelen "et rom", er notasjonen 1/4, der tallet over linjen er telleren og den nedenfor er nevneren.
Når du snakker om brøk, snakker du virkelig om delene der helheten av noe må deles. Tallene som utgjør en brøkdel er hel.
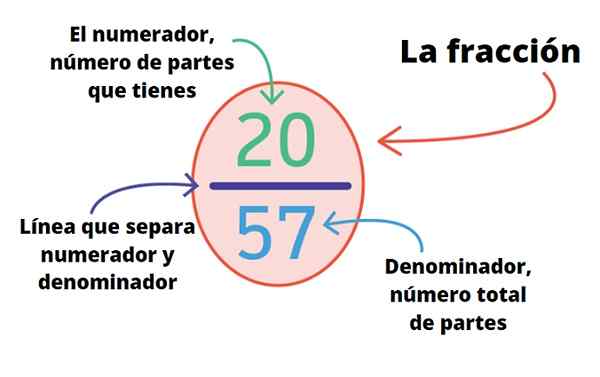
Derfor er delene av brøkdelen:
- Telleren (øvre del).
- Nevneren (nedre del).
Definisjon
Den formelle matematiske definisjonen av brøk er: settet som er dannet av alle elementene i P/Q -formen, der "P" og "Q" er heltall med "Q" forskjellige fra null.
Dette settet kalles settet med rasjonelle tall. Rasjonelle tall kalles også ødelagte tall.
Gitt et hvilket som helst rasjonelt antall i sitt desimale uttrykk, kan du alltid få brøkdelen som genererer den.
Eksempler på bruk av brøk
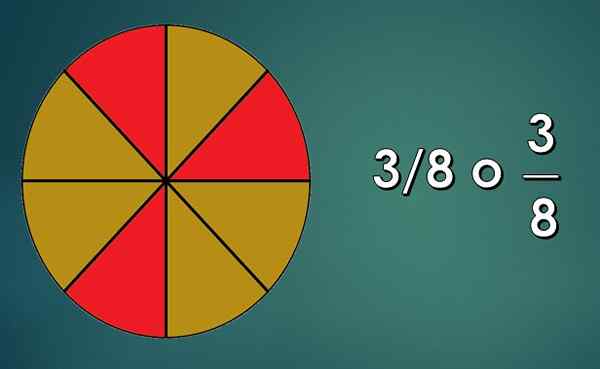 3 deler av 8
3 deler av 8 Den grunnleggende måten de lærer et barn begrepet en brøkdel er ved å distribuere delene av et objekt, eller et sett med objekter. For eksempel:
Bursdagskake
Hvis du vil dele en sirkulær bursdagskake mellom 8 barn slik at alle barn får samme mengde kake.
Kan tjene deg: Freedoms grader: Hvordan beregne dem, typer, eksemplerDet begynner med å dele denne kaken i 8 like deler som i figuren nedenfor. Deretter distribueres hvert barn et kake stykke.
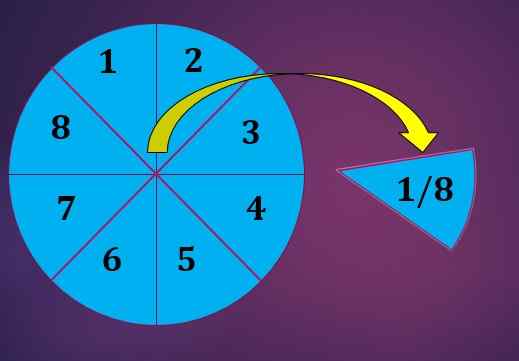
Måten å representere brøkdelen (delen) av kaken som berørte hvert barn er 1/8, der telleren er 1, siden hvert barn bare fikk ett kakestykke og nevneren er 8, siden kaken ble kuttet i 8 lik deler.
Godteri
Maria kjøpte 5 godteri til sine to barn. Han ga Juan 2 godteri og Rosa ga 3 godteri.
Det totale godteriet er 5 og må distribueres 5. I følge distribusjonen som María gjorde, berørte Juan 2 godteri på 5 totalt, så brøkdelen av godteri han fikk er 2/5.
Ettersom Rosa fikk 3 godteri av totalt 5 karameller, var brøkdelen av karameloer som Rosa fikk 3/5.

Rektangulær nær
Roberto og José må male et rektangulært gjerde som er delt inn i 17 vertikale tabeller med like dimensjoner som vist på figuren nedenfor. Hvis Roberto malte 8 bord, hvilken brøkdel av gjerdet malte José?
De totale vertikale tabellene med samme størrelse i gjerdet er 17. Brøkdelen av gjerdet som Roberto malte er oppnådd ved hjelp av antall tabeller malt av Roberto og nevneren er det totale antallet tabeller, det vil si 17.
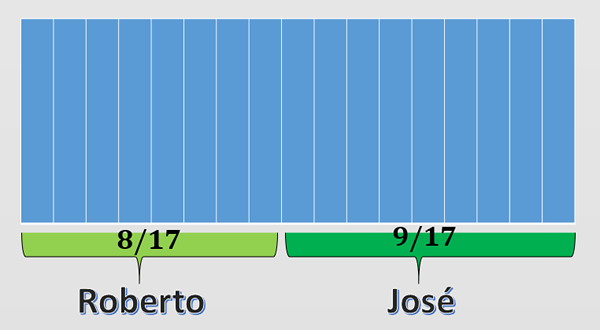
Deretter var brøkdelen av gjerdet malt av Roberto 8/17. For å fullføre alt gjerdet, trenger 9 flere bord å male.
Disse 9 bordene ble malt av José. Dette indikerer at brøkdelen av gjerdet som José malte var 9/17.
Kan tjene deg: i påvente av en linje: formel og ligninger, representasjon, eksemplerReferanser
- Almaguer, g. (2002). Matematikk 1. Redaksjonell Limusa.
- Bussell, l. (2008). Pizza i deler: brøk! Gareth Stevens.
- Cofré, a., & Tapia, l. (nitten nitti fem). Hvordan utvikle matematisk logisk resonnement. Universitetets redaksjon.
- Fra sjø. (1962). Matematikk for verkstedet. REVERTE.
- Lira, m. L. (1994). Simon og matematikk: Matematikk Tekst for andre grunnleggende år: Studentbok. Andres Bello.
- Palmer, c. Yo., & Bibb, S. F. (1979). Praktisk matematikk: Aritmetikk, algebra, geometri, trigonometri og beregningsregel (Reprint Ed.). REVERTE.
- « Hydrostatisk trykkformel, beregning, eksempler, øvelser
- Historie med trigonometri fra sin opprinnelse »

