Påskeprinsipphistorie, applikasjoner, eksempler

Han Pascal -prinsippet, o Pascal lov, fastslår at en endring i trykket fra en væske innesperret i noen av punktene overføres uten endring til alle andre punkter i væsken.

Dette prinsippet ble oppdaget av den franske forskeren Blaise Pascal (1623 - 1662). På grunn av viktigheten av bidrag fra Pascal til vitenskapen, er pressenheten i det internasjonale systemet blitt utnevnt til sin ære.

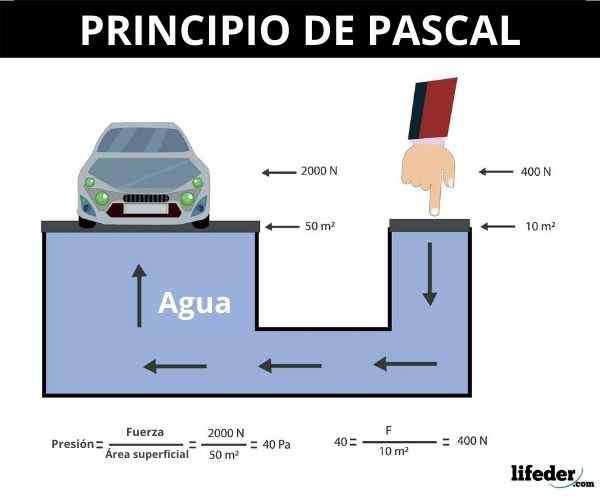
Siden trykket er definert som kvotienten mellom kraften vinkelrett på et område mellom området, tilsvarer 1 Pascal (PA) 1 Newton / M².

[TOC]

Historie

For å bekrefte prinsippet, utviklet Pascal en ganske overveldende demonstrasjon. Han tok en hul sfære og gjennomboret flere steder, satte luer i alle hullene bortsett fra i ett, som han fylte den med vann. I dette plasserte han en sprøyte utstyrt med et stempel.

Ved å øke trykket i stemplet tilstrekkelig, blir hettene skutt samtidig, fordi trykket overføres likt til alle punktene i væsken og i alle retninger, og dermed demonstrerer Pascal lov.

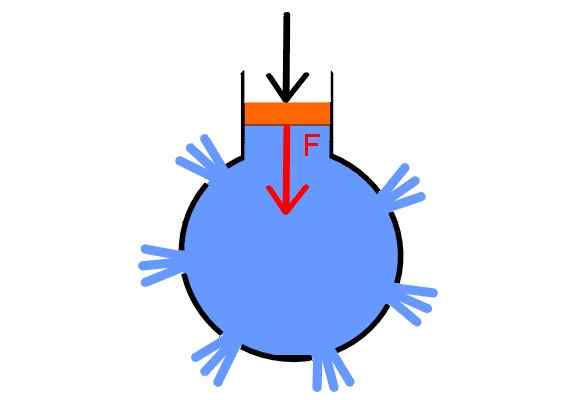Pascal sprøyte. Kilde: Wikimedia Commons.

Blaise Pascal hadde et kort liv, preget av sykdommen. Den utrolige rekkevidden for tankene hans førte til at han undersøkte forskjellige aspekter av natur og filosofi. Hans bidrag var ikke begrenset til å studere atferden til væsker, Pascal var også en pioner for databehandling.

Og i en alder av 19 år opprettet Pascal en mekanisk kalkulator for faren å bruke henne i sitt arbeid i Frankrikes skattesystem: den Pascalina.

Sammen med sin venn og kollega formet også den store matematikeren Pierre of Fermat teorien om sannsynligheter, uunnværlig i fysikk og statistikk. Pascal døde i Paris, i en alder av 39 år.

Forklaring av Pascal -prinsippet

Neste eksperiment er ganske enkelt: et U -rør er fylt med vann og luene plasseres i hver ende som kan gli jevnt og enkelt, som et stempel. Det er trykk mot venstre stempel som synker litt, og det observeres at den til høyre stiger, skyvet av væsken (nedre figur).

Kan tjene deg: Andromeda: oppdagelse, opprinnelse, egenskaper, struktur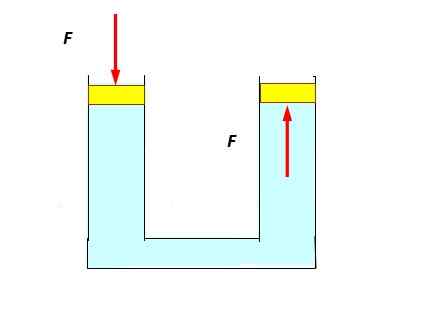Anvendelse av Pascal -prinsippet. Kilde: Selvlaget.

Dette skjer fordi trykket overføres uten noen reduksjon til full punkt av væsken, inkludert de som er i kontakt med høyre stempel.

Væsker som vann eller olje er inkomprimerbare, men samtidig har molekylene nok bevegelsesfrihet, noe som gjør det mulig for trykket å distribueres på høyre stempel.

Takket være dette mottar høyre stempel en kraft som er nøyaktig den samme i størrelsesorden og retning som det ble påført til venstre, men av motsatt retning.

Trykket i en statisk væske er uavhengig av formen på beholderen. Det vil umiddelbart bli demonstrert at trykket varierer lineært med dybden og prinsippet om Pascal er en konsekvens av dette.

En endring av trykket når som helst, gjør at trykket på et annet punkt endrer i samme mengde. Ellers ville det være et ekstra trykk som ville strømme væsken.

Forholdet mellom trykk og dybde

En hvilevæske utøver en kraft på veggene i beholderen som inneholder den og også på overflaten av ethvert objekt nedsenket i den. I eksperimentet med Pascal -sprøyten ser man at vannspruten kommer ut vinkelrett Til sfæren.

Væskene fordeler kraften vinkelrett på overflaten den virker på, så det er praktisk å innføre konseptet med gjennomsnittlig trykk P_m som den vinkelrett kraften utøvd F_⊥ Etter område TIL, hvis enhet er Pascal:

P_m = F_⊥ / TIL

Trykket øker med dybden. Du kan se en liten del av statisk likevektsvæske og bruke Newtons andre lov:

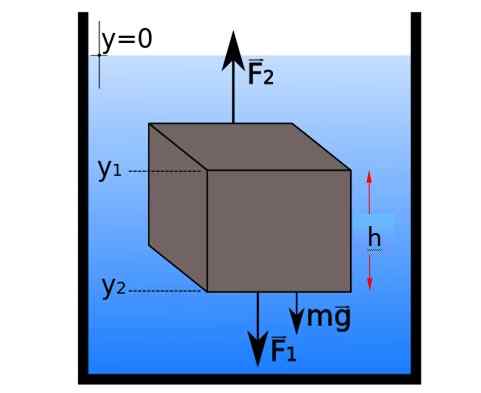Gratis kroppsdiagram over en liten del av statisk likevekt med en kube -formet. Kilde: E-XUAO [CC BY-SA 4.0 (https: // creativecommons.Org/lisenser/by-SA/4.0)]

Horisontale krefter avlyses av par, men i vertikal retning er kreftene gruppert som følger:

∑f_og = F₂ - F₁ - mg = 0 → F₂ - F₁ = mg

Uttrykke deigen når det gjelder tetthet ρ = masse /volum:

P₂.A- s₁.A = ρ X volum x g

Volumet til væskedelen er produktet ved x h:

Det kan tjene deg: Second Law of Thermodynamics: Formler, ligninger, eksempler

TIL.(S₂ - P₁) = ρ X a x h x g

ΔP = ρ.g.h   Grunnleggende teorem om hydrostatisk

applikasjoner

En traktorgraver bruker Pascal -prinsippet for å løfte store pesos

Pascal -prinsippet har blitt brukt til å bygge mange enheter som multipliserer styrke og letter oppgaver som å løfte pesos, stempling på metall eller trykke på objekter. Blant dem er:

-Den hydrauliske pressen

-Bilbremsesystemet

-Mekaniske spader og mekaniske armer

-Den hydrauliske katten

-Kraner og heiser

Neste, la oss se hvordan Pascal -prinsippet får små krefter til å forvandle seg til store krefter for å utføre alle disse verkene. Den hydrauliske pressen er det mest karakteristiske eksemplet og vil bli analysert nedenfor.

Den hydrauliske pressen

For å bygge en hydraulisk presse er den samme enheten til den øvre figuren tatt, det vil si en U -formet beholder, som vi allerede vet at den samme kraften overføres fra ett stempel. Forskjellen vil være størrelsen på stemplene, og det er dette som får enheten til å fungere.

Følgende figur viser Pascal -prinsippet i aksjon. Trykket er det samme på alle punktene i væsken, både i det lille og store stempelet:

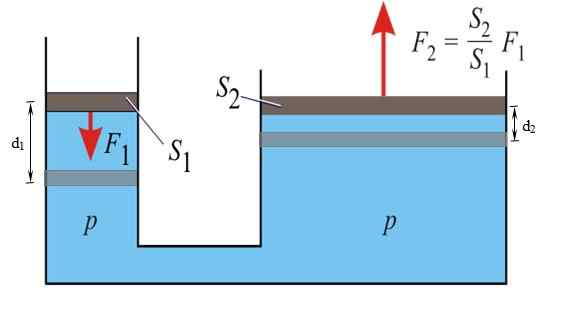Hydraulisk presseopplegg. Kilde: Wikimedia Commons.

p = f₁ / S₁ = F₂ / S₂

Størrelsen på kraften som overføres til det store stempelet er:

F₂ = (S₂ / S₁). F₁

Som s₂ > S₁, resulterer i f₂ > F₁, Derfor har utgangskraften multiplisert i faktoren gitt av kvotienten mellom områdene.

Eksempler

Denne delen viser applikasjonseksempler.

Hydrauliske bremser

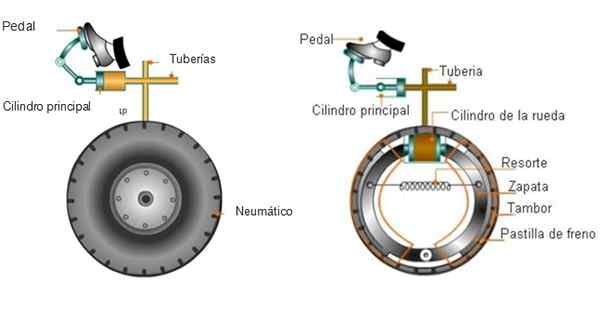
Bilbremser benytter seg av Pascal -prinsippet gjennom en hydraulisk væske som fyller noen rør koblet til hjulene. Når du trenger å stoppe, bruker sjåføren en styrke ved å undertrykke bremsepedalen og generere et trykk på væsken.

I den andre enden skyver trykket bremseklossene mot trommelen eller bremseskivene som svinger sammen med hjulene (ikke med dekkene). Den resulterende friksjonen gjør at platen stopper, og bremser også hjulene.

Kan tjene deg: Mekaniske bølger: Kjennetegn, egenskaper, formler, typerHydraulisk bremsesystem. Kilde: f. Zapata

Mekanisk fordel med den hydrauliske pressen

I den hydrauliske pressen til den nedre figuren, må inngangsarbeidet være lik utgangsarbeidet så lenge friksjon ikke blir tatt i betraktning.

Inngangskraften F₁ Får stempelet til å reise en avstand d₁ Når du går ned, mens utgangskraften F₂ Tillater en d₂ av stempelet som går opp. Hvis det mekaniske arbeidet utført av begge kreftene er det samme:

F₁.d₁ = F₂. d₂

Den mekaniske fordelen m er kvotienten mellom størrelsene på inngangs- og utgangskraften:

M = f₂/F₁ = d₁/d₂

Og som demonstrert i foregående avsnitt, kan det også uttrykkes som kvotienten mellom områdene:

F₂/F₁ = S₂ / S₁

Det ser ut til at arbeidet gjøres gratis, men det skaper egentlig ikke energi med denne enheten, siden den mekaniske fordelen oppnås på bekostning av forskyvning av det lille stempelet D₁.

Så for å optimalisere ytelsen, blir et ventilsystem lagt til enheten på en slik måte at utgangsstempelet heves takket være korte impulser på inngangsstempelet.

På denne måten pumper operatøren av en garasjehydraulisk katt flere ganger for å gradvis løfte et kjøretøy.

Trening løst

I den hydrauliske pressen i figur 5 er områdene til stemplene 0.5 kvadratmeter (lite stempel) og 25 kvadratmeter (stort stempel). Finne:

a) Den mekaniske fordelen med denne pressen.

b) Den nødvendige kraften for å løfte en belastning på 1 tonn.

c) Avstanden som inngangskraften må fungere for å løfte nevnte belastning på 1 tomme.

Uttrykke alle resultatene i enheter i det britiske systemet og det internasjonale systemet hvis.

Løsning

a) Den mekaniske fordelen er:

M = f₂/F₁ = S₂/S₁ = 25 tommer² / 0.5 in² = 50

b) 1 tonn tilsvarer 2000 lb-kraft. Den nødvendige styrken er f₁:

F₁ = F₂ / M = 2000 lb-kraft / 50 = 40 lb-kraft

For å uttrykke resultatet i det internasjonale systemet, kreves følgende konverteringsfaktor:

1 lb-force = 4.448 n

Derfor er størrelsen på F1 177.92 n.

c) M = d₁/d_{2 →} d₁ = M.d₂ = 50 x 1 in = 50 in

Den nødvendige konverteringsfaktoren er: 1 in = 2.54 cm

d₁ = 127 cm = 1.27 m

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 417-450.
2. College Physics. Pascals prinsipp. Gjenopprettet fra: OpenTextBc.Ac.
3. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 4. Væsker og termodynamikk. Redigert av Douglas Figueroa (USB). 4 - 12.
4. Rex, a. 2011. Fundamentals of Physics. Pearson. 246-255.
5. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. McGraw Hill.301-320.