Betinget sannsynlighetsformel og ligninger, egenskaper, eksempler

De betinget sannsynlighet Det er muligheten for forekomst av en viss hendelse, siden en annen forekommer som en tilstand. Denne tilleggsinformasjonen kan endre (eller kanskje ikke) oppfatningen om at noe vil skje.

For eksempel kan vi spørre oss selv: “Hva er sannsynligheten for at det regner i dag, siden det ikke regner for to dager siden?"". Hendelsen vi ønsker å vite sannsynligheten er at det regner i dag, og tilleggsinformasjonen som vil betinget svaret er at "for to dager siden det ikke regner".

Figur 1. Sannsynligheten for at det regner i dag siden det regnet i går er også et eksempel på betinget sannsynlighet. Kilde: Pixabay.

Være en Probabilistisk rom sammensatt av ω (prøveområde), ℬ (tilfeldige hendelser) og p (sannsynligheten for hver hendelse), pluss hendelser A og B som tilhører ℬ.

Den betingede sannsynligheten som oppstår, siden B, som er betegnet som P (A│B), er definert på denne måten:

P (A│B) = P (A∩B) / P (B) = P (A og B) / P (B)

Hvor: p (a) er sannsynligheten for forekomst av a, p (b) er sannsynligheten for hendelse b og er forskjellig fra 0, og p (a∩b) er sannsynligheten for skjæringspunktet mellom a og b, det vil si , sannsynligheten for at begge hendelsene oppstår (felles sannsynlighet).

Dette er et uttrykk for Bayes -teoremet brukt på to hendelser, foreslått i 1763 av den engelske teologen og matematikeren Thomas Bayes.

[TOC]

Egenskaper

-All betinget sannsynlighet er mellom 0 og 1:

0 ≤ P (A│B) ≤ 1

-Sannsynligheten for at hendelsen vil skje, siden denne hendelsen skjer, er åpenbart 1:

P (a│a) = p (a∩a) / p (a) = p (a) / p (a) = 1

-Hvis to hendelser er eksklusive, det vil si hendelser som ikke kan skje samtidig, er den betingede sannsynligheten for at en av dem skjer 0, siden krysset er ugyldig:

P (a│b) = p (a∩b) / p (b) = 0 / p (b) = 0

-Hvis B er en delmengde av A, er den betingede sannsynligheten også 1:

Kan tjene deg: Toroid eller Toro Dona

P (B│a) = P (A∩B) / P (A) = 1

Viktig

P (A│B) Det er generelt ikke lik P (B│A), derfor må du passe på å ikke utveksle hendelser når du finner betinget sannsynlighet.

Generell regel om multiplikasjon

Mange ganger vil du finne den felles sannsynligheten P (A∩B), i stedet for betinget sannsynlighet. Så gjennom følgende teorem har du:

P (A∩B) = P (A og B) = P (A│B). P (B)

Teoremet kan utvides for tre hendelser A, B og C:

P (a∩b∩c) = p (a og b og c) = p (a) · p (b│a) · p (c│a∩b)

Og også for flere arrangementer, for eksempel₁, TIL₂, TIL₃ Og mer, det kan uttrykkes som følger:

P (a₁∩ a₂ ∩ a₃… ∩ A_n) = P (a₁) . P (a₂│a₁). P (a₃│a₁∩ a₂) ... P (a_n│a₁∩ a₂∩… a_N-1)

Når det er tilfelle av hendelser som oppstår i rekkefølge og gjennom forskjellige stadier, er det praktisk å organisere dataene i et diagram eller tabell. Dette letter visualisering av alternativene for å nå den forespurte sannsynligheten.

Eksempler på dette er trediagram og beredskapstabell. Fra en av dem kan du bygge den andre.

Eksempler på betinget sannsynlighet

La oss se på noen situasjoner der sannsynligheten for en hendelse blir endret av forekomsten av en annen:

- Eksempel 1

I en søt butikk selges to typer kaker: jordbær og sjokolade. Når du registrerte preferansene til 50 klienter av begge kjønn, ble følgende verdier bestemt:

-27 kvinner, hvorav 11 foretrekker jordbær og 16 sjokoladekake.

-23 menn: 15 sjokolade og 8 jordbær.

Sannsynligheten for at en kunde velger en sjokoladekake kan bestemmes ved å bruke Laplace -regelen, i henhold til hvilken sannsynlighet for enhver hendelse er:

P = antall gunstige hendelser/Totalt antall hendelser

I dette tilfellet, av 50 klienter, foretrekker totalt 31 sjokolade, slik at sannsynligheten vil være p = 31/50 = 0.62. Det vil si at 62% av kundene foretrekker sjokoladekake.

Kan tjene deg: Polynomligninger

Men ville det være annerledes hvis klienten er en kvinne? Dette er et tilfelle av betinget sannsynlighet.

Beredskapstabell

Gjennom en beredskapstabell som dette blir totalene enkelt visualisert:

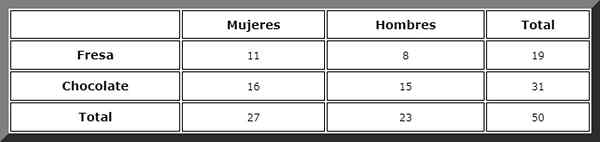
Deretter blir de gunstige tilfellene observert og Laplace -regelen blir brukt, men før vi definerer hendelsene:

-B er "kvinneklienten" -arrangementet.

-A er arrangementet "foretrekker sjokoladekake" å være kvinne.

Vi går til kolonnen merket "Kvinner" og der ser vi at totalen er 27.

Da blir den gunstige saken søkt i "sjokolade" -rekken. Det er 16 hendelser av disse, derfor er den etterspurte sannsynligheten direkte:

P (A│B) = 16/27 = 0.5924

A 59.24 % av kvinnene kvinner foretrekker sjokoladekake.

Denne verdien sammenfaller når vi står i kontrast til den opprinnelig gitte definisjonen av betinget sannsynlighet:

P (A│B) = P (A∩B) / P (B)

Vi forsikrer oss gjennom Laplace -regelen og verdiene på tabellen:

P (b) = 27/50

P (A og B) = 16/50

Der P (A og B) er sannsynligheten for at klienten foretrekker sjokolade og er kvinne. Nå erstattes verdiene:

P (A│B) = P (A og B)/P (B) = (16/50)/(27/50) = 16/27 = 0.5924.

Og det er bevist at resultatet er det samme.

- Eksempel 2

I dette eksemplet gjelder multiplikasjonsregelen. Anta at det i utstillingen av en butikk er bukser i tre størrelser: små, mellomstore og store.

I mye med totalt 24 bukser, hvorav det er 8 av hver størrelse og alle er blandede. Hva ville være sannsynligheten for å trekke ut to av dem og at begge var små?

Det er tydelig at sannsynligheten for å trekke ut små bukser i første forsøk er 8/24 = 1/3. Nå er den andre ekstraksjonen betinget av den første hendelsen, siden når du tar ut bukser, er det ikke lenger 24, men 23. Og hvis en liten bukse fjernes, er det 7 i stedet for 8.

Kan tjene deg: Multiplikativ prinsipp: telleteknikker og eksempler

Arrangement A er å ta ut en liten bukse, etter å ha tatt en annen i første forsøk. Og hendelsen B er småbukser til den første. Derfor:

P (b) = 1/3; P (A│B) = 7/24

Til slutt, gjennom multiplikasjonsregelen:

P (A∩B) = (7/24).(1/3) = 7/72 = 0.097

Trening løst

I en studie av punktlighet på kommersielle luftflyvninger er følgende data tilgjengelig:

-P (b) = 0.83, er sannsynligheten for at et fly tar å ta en betimelig.

-P (a) = 0.81, er sannsynligheten for å lande i tide.

-P (b∩a) = 0.78 Det er sannsynligheten for at flyturen kommer i tide å ta en rettidig.

Det blir bedt om å beregne:

a) Hva er sannsynligheten for at flyet lander omgående siden det tok av i tide?

b) Sannsynligheten ovenfor er den samme som sannsynligheten for at den har kommet ut i tide hvis du klarte å lande omgående?

c) og til slutt: hva er sannsynligheten for at det vil komme i tide siden det ikke kom ut i tide?

Figur 2. Punktlighet på kommersielle flyreiser er viktig, siden forsinkelser genererer millionær tap. Kilde: Pixabay.

Løsning på

For å svare på spørsmålet brukes definisjonen av betinget sannsynlighet:

P (a│b) = p (a∩b) / p (b) = p (a og b) / p (b) = 0.78/0.83 = 0.9398

Løsning b

I dette tilfellet utveksles hendelser i definisjonen:

P (b│a) = p (a∩b) / p (a) = p (a og b) / p (a) = 0.78/0.81 = 0.9630

Merk at denne sannsynligheten er litt forskjellig fra den forrige, som vi tidligere antydet.

Løsning c

Sannsynligheten for ikke å være punktlig er 1 - P (b) = 1 - 0,83 = 0.17, vi vil kalle det P (B^C), Fordi det er den komplementære hendelsen å ta en betimelig. Den betingede sannsynligheten som ble søkt er:

P (A│B^C) = P (A∩B^C) / P (B^C) = P (A og B^C)/P (B^C)

På den andre siden:

P (A∩B^C) = P (tidslanding) - P (tidslanding og kikk ta av) = 0.81-0.78 = 0.03

I dette tilfellet er sannsynligheten som ble søkt:

P (A│B^C) = 0.03/0.17 = 0.1765

Referanser

1. Canavos, g. 1988. Sannsynlighet og statistikk: applikasjoner og metoder. McGraw Hill.
2. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørfag og vitenskap. 8. Utgave. Cengage.
3. Lipschutz, s. 1991. Schaum Series: Sannsynlighet. McGraw Hill.
4. Obregón, i. 1989.Teori om sannsynlighet. Redaksjonell Limusa.
5. Walpole, r. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.
6. Wikipedia. Betinget sannsynlighet. Gjenopprettet fra: er.Wikipedia.org.