Teoretisk sannsynlighet for hvordan du får det ut, eksempler, øvelser

De Teoretisk sannsynlighet (eller av Laplace) at det oppstår en hendelse som tilhører et utvalgsrom, der alle hendelser har samme sannsynlighet for forekomst, det er definert i matematisk notasjon som: P (e) = n (e) / n ( S)

Hvor P (e) er sannsynligheten, gitt som forholdet mellom det totale antall mulige resultater av E -hendelsen, som vi kaller N (e), delt på det totale antallet N (S) for mulige resultater i prøveområdet S.

Figur 1. Ved lanseringen av en seks -sidig terninger er den teoretiske sannsynligheten for at ansiktet med tre prikker er øverst ⅙. Kilde: Pixabay.

Den teoretiske sannsynligheten er et reelt tall mellom 0 og 1, men det kommer ofte til uttrykk i form av en prosentandel, i hvilket tilfelle vil sannsynligheten være en verdi mellom 0% og 100%.

Å beregne sannsynligheten for forekomst av en hendelse er veldig viktig på mange felt, for eksempel aksjemarkedsaktivitet, forsikringsselskaper, pengespill og mange flere.

[TOC]

Hvordan få den teoretiske sannsynligheten?

En illustrerende sak er tilfellet med rifas eller lotterier. Anta at 1.000 billetter til Rifar en smarttelefon. Ettersom tombola gjøres tilfeldig, har noen av billettene samme sjanse til å være en vinner. 

For å finne sannsynligheten for at en person som kjøper en billett med nummer 81, er vinner, følgende beregning av Teoretisk sannsynlighet:

P (1) = 1/1.000 = 0,001 = 0,1%

Det forrige resultatet tolkes som følger: Hvis tombola gjentas uendelig, hver 1.000 ganger billett 81 vil i gjennomsnitt bli valgt en gang.

Hvis noen av en eller annen grunn skaffer seg alle billetter, er det sikkert at han vil vinne prisen. Sannsynligheten for å vinne prisen hvis du har alle billetter beregnet som følger:

Det kan tjene deg: omkretsen av sirkelen: Hvordan ta den ut og formler, løste øvelser

P (1.000) = 1.000/1.000 = 1 = 100%.

Det vil si hvilken sannsynlighet 1 eller 100% betyr at det er helt sikkert at dette resultatet vil oppstå.

Hvis noen har 500 billetter, er mulighetene for å vinne eller tape de samme. Den teoretiske sannsynligheten for å vinne prisen i denne saken beregnes som følger:

P (500) = 500/1.000 = ½ = 0,5 = 50%.

Han som ikke kjøper noen billett, har ingen sjanse til å vinne, og hans teoretiske sannsynlighet bestemmes slik:

 P (0) = 0/1.000 = 0 = 0%

Eksempler

Eksempel 1

Du har en valuta med dyrt på den ene siden og skjold eller forsegle i den andre. Når valutaen lanseres, hva er den teoretiske sannsynligheten for å være dyr?

P (dyrt) = n (dyrt) / N ( ansikt + skjold ) = ½ = 0,5 = 50%

Resultatet tolkes som følger: Hvis det ble gjort et stort antall utgivelser, i gjennomsnitt i hver 2. plassering, ville en av dem møte.

Prosentvis vilkår er tolkningen av resultatet at det å gjøre et uendelig stort antall lanseringer, i gjennomsnitt hver 100 av dem 50 vil resultere i dyrt.

Eksempel 2

I en boks er det 3 blå klinkekuler, 2 røde klinkekuler og 1 grønn. Hva er den teoretiske sannsynligheten for at når du får en marmor fra boksen, er dette rødt?

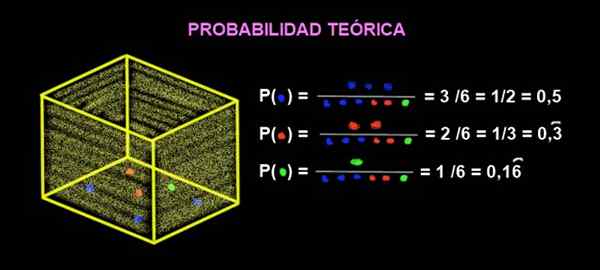Figur 2. Sannsynlighet for utvinning av fargekuler. Kilde: f. Zapata.

Sannsynligheten som kommer rødt er:

P (rød) = antall gunstige tilfeller / antall mulige saker

Det er å si:

P (rød) = antall røde klinkekuler / totalt antall kuler

Endelig sannsynligheten for at en rød marmor er:

P (rød) = 2/6 = ⅓ = 0,3333 = 33,33%

Mens sannsynligheten for at ved å trekke ut en grønn marmor er:

P (grønn) = ⅙ = 0,1666 = 16,66%

Til slutt er den teoretiske sannsynligheten for å oppnå i en blind ekstraksjon en blå marmor: 

P (blå) = 3/6 = ½ = 0,5 = 50%

Det kan tjene deg: radikale egenskaper

Det vil si at av hver 2 forsøk vil resultatet være blå i en av dem og en annen farge i et annet forsøk, under forutsetningen om at den ekstraherte marmoren blir etterfylt og at antallet forsøk er veldig, veldig stort.

Øvelser

Oppgave 1

Bestem sannsynligheten for at når du starter en terning, oppnås en verdi mindre enn eller lik 4.

Løsning

For å beregne sannsynligheten for at denne hendelsen skjer, vil definisjonen av teoretisk sannsynlighet gjelde:

P (≤4) = antall gunstige tilfeller / antall mulige tilfeller

P (≤5) = 5/6 = = 83,33%

Oppgave 2

Finn sannsynligheten for at i to påfølgende plasser av en normal seks -sidig terning, 2 ganger 2 ganger.

Løsning

For å svare på denne øvelsen er det praktisk å lage et bilde for å vise alle mulighetene. Den første figuren indikerer resultatet av den første terningen og den andre resultatet av den andre.

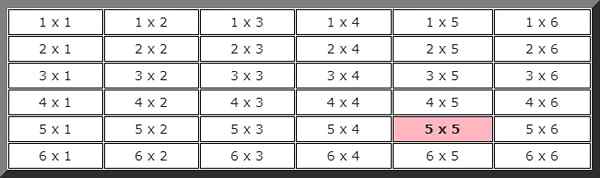
For å beregne den teoretiske sannsynligheten vi trenger å vite det totale antallet mulige tilfeller, i dette tilfellet som det kan sees fra forrige tabell, er det 36 muligheter.

Observasjon av maleriet følger også at antallet tilfeller som er gunstig for hendelsen som i de to påfølgende utgivelsene kommer 5 er bare 1, fremhevet med farge, derfor er sannsynligheten for at denne hendelsen vil skje:

P (5 x 5) = 1/33.

Dette resultatet kunne også vært nådd ved bruk av en av egenskapene til teoretisk sannsynlighet, som sier at den samlede sannsynligheten for to uavhengige hendelser er et produkt av deres individuelle sannsynligheter.

I dette tilfellet er sannsynligheten for at i den første utgivelsen 5 er ⅙. Den andre lanseringen er helt uavhengig av den første, derfor er sannsynligheten for at 5 i den andre også ⅙. Så den kombinerte sannsynligheten er:

Kan tjene deg: Delvis derivater: egenskaper, beregning, øvelser

P (5 × 5) = P (5) P (5) = (1/6) (1/6) = 1/36.

Øvelse 3

Finn sannsynligheten for at et tall mindre enn 2 kommer ut i den første lanseringen og i det andre et nummer større enn 2 kommer ut. 

Løsning

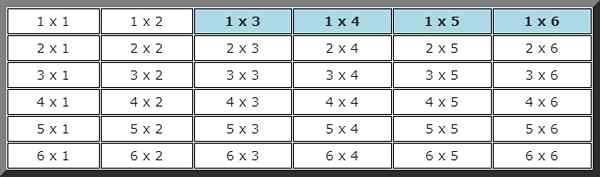
Igjen må du bygge et mulig arrangementstabell, der de første lanseringen var mindre enn 2 og i det andre høyere enn 2 er understreket.

Totalt er det 4 muligheter for totalt 36. Med andre ord, sannsynligheten for denne hendelsen er:

P (2) = 4/36 = 1/9 = 0,1111 = 11,11%

Bruke sannsynlighetsteoremet som sier:

Sannsynligheten for forekomst av to uavhengige hendelser er lik produktet av individuelle sannsynligheter.

Det oppnås identisk resultat:

P (2) = (1/6) (4/6) = 4/36 = 0.1111 = 11.11%

Verdien oppnådd med denne prosedyren sammenfaller med det forrige resultatet, gjennom den teoretiske eller klassiske definisjonen av sannsynlighet.

Oppgave 4

Hva er sannsynligheten for at ved å starte to gitt summen av verdiene er 7.

Løsning

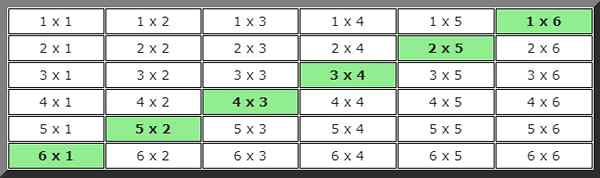
For å finne løsningen i dette tilfellet, er det utviklet et bilde av muligheter der tilfellene som oppfyller tilstanden til verdiene er 7, er indikert i farger.

Når vi ser på tabellen, kan 6 mulige tilfeller telles, så sannsynligheten er:

P (FoU II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%

Referanser

1. Canavos, g. 1988. Sannsynlighet og statistikk: applikasjoner og metoder. McGraw Hill.
2. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørfag og vitenskap. 8. Utgave. Cengage.
3. Lipschutz, s. 1991. Schaum Series: Sannsynlighet. McGraw Hill.
4. Obregón, i. 1989.Teori om sannsynlighet. Redaksjonell Limusa.
5. Walpole, r. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.