Politropiske prosessegenskaper, applikasjoner og eksempler

EN Politropisk prosess Det er en termodynamisk prosess som oppstår når forholdet mellom trykk P og volumet V gitt av P.Vⁿ Det forblir konstant. Eksponenten n Det er et reelt tall, generelt mellom null og uendelig, men at i noen tilfeller kan være negativt.

Verdien av n motta navnet på Politropy Index Og det er viktig å fremheve at under en polytropisk termodynamisk prosess nevnte indeksen må opprettholde en fast verdi, ellers vil prosessen ikke bli betraktet som polytropisk.

Figur 1. Karakteristisk ligning av en polytrop termodynamisk prosess. Kilde: f. Zapata.

[TOC]

Kjennetegn på polytropiske prosesser

Noen karakteristiske tilfeller av polytropiske prosesser er: 

- Den isotermiske prosessen (ved konstant T -temperatur), der eksponenten er n = 1.

- En isobarisk prosess (konstant trykk P), i dette tilfellet n = 0.

- Den isokoriske prosessen (til volum V konstant), for hvilken+∞.

- Adiabatiske prosesser (til konstant entropi), der eksponenten er n = γ, er γ den adiabatiske konstanten. Denne konstanten er kvotienten mellom varmekapasiteten ved konstant trykk CP delt på varmekapasiteten ved konstant CV -volum:

γ = cp/cv

- Enhver annen termodynamisk prosess som ikke er noen av de tidligere tilfellene. Men følg P.Vⁿ = CTTE Med ekte og konstant polytropisk indeks n Det vil også være en polytropisk prosess.

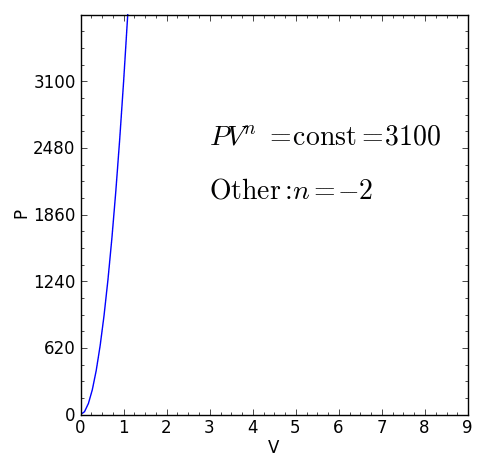Figur 2. Ulike karakteristiske tilfeller av polytropiske termodynamiske prosesser. Kilde: Wikimedia Commons.

applikasjoner

En av de viktigste anvendelsene av den polytropiske ligningen er for beregningen av arbeidet utført av et lukket termodynamisk system, når det går fra en innledende tilstand til en annen ende på en kvasi -statisk måte, det vil si etter en rekke likevektstilstander.

Arbeid i polytropiske prosesser for forskjellige verdier av n

For n ≠ 1

Mekanisk arbeid w utført av et lukket termodynamisk system beregnes ved uttrykk:

W = ∫p.Dv

Kan tjene deg: Diamagnetisme: Materialer, applikasjoner, eksempler

Hvor p er trykket og v volumet.

Som i tilfelle av en polytropisk prosess er forholdet mellom trykk og volum:

P.V ⁿ = konstant = C

Rydde P for det forrige uttrykket for å erstatte det i uttrykk for arbeid:

P = c /V ⁿ

Du har gjort det mekaniske arbeidet under en polytropisk prosess, som begynner i en innledende tilstand 1 og slutter i den endelige tilstanden 2. Alt dette vises i følgende uttrykk:

Hvis n ≠ 1, har du:

I tillegg, ettersom de innledende og endelige tilstandene er godt definert, bestemmes også konstanten av følgende uttrykk:

C = s₁ V₁ⁿ = S₂ V₂ⁿ

Ved å erstatte verdien av konstanten i uttrykk for arbeid oppnås:

W = (P₂ V₂ - P₁ V₁)/(1-n)

I tilfelle arbeidsstoffet kan modelleres som en ideell gass, er følgende tilstandsligning:

P.V = m.R.T

Hvor m er antall mol ideell gass og r er den universelle konstanten av gasser.

For en ideell gass som følger en polytropisk prosess med en polytropiindeks som er forskjellig fra enheten, og som går fra en tilstand med starttemperatur t₁ til en annen tilstand med temperatur t₂ Arbeidet som er utført er gitt av følgende formel:

W = m r (t₂ - T₁)/(1-n)

For n → ∞

I henhold til formelen for arbeidet som er oppnådd i forrige seksjon, er arbeidet med en polytropisk prosess med n = ∞ null, fordi uttrykk for arbeid er delt mellom uendelig og derfor har resultatet en tendens til null.

En annen måte å nå dette resultatet er å starte fra P -forholdet₁ V₁ⁿ = S₂ V₂ⁿ, som kan skrives om som følger:

(S₁/S₂) = (V₂/V1)ⁿ

Tar N-tykk rot i hvert medlem du får:

(V₂/V1) = (P₁/S₂)^(1/n)

I tilfelle at n → ∞, må du (v₂/V1) = 1, som betyr at:

Kan tjene deg: avsagt varme: Formler, hvordan du beregner det og løste øvelser

V₂ = V₁

Det vil si at volumet ikke endres i en polytropisk prosess med N → ∞. Derfor er DV -volumdifferensialet i integralen av mekanisk arbeid 0. Disse typene polytropiske prosesser er også kjent som prosesser isokorisk, o Prosesser med konstant volum.

For n = 1

Igjen har vi uttrykket for arbeid:

W = ∫p dv

I tilfelle av en polytropisk prosess med n = 1, er forholdet mellom trykk og volum:

P v = konstant = c

Ved å rydde P for det forrige uttrykket og utskifting, har du arbeidet gjort for å gå fra den opprinnelige tilstanden 1 til den endelige tilstanden 2:

W = ∫12p dv = ctt ∫12 v^( - 1) dv = ctt (ln (v2) - ln (v1))

Det er å si:

W = c ln (v₂/V₁).

Ettersom de første og endelige tilstandene er godt bestemt, vil også CTTE. Det er å si:

C = s₁ V₁ = S₂ V₂

Til slutt er følgende nyttige uttrykk tilgjengelige for å finne det mekaniske arbeidet til et polyitropisk lukket system der n = 1.

W = s₁ V₁ LN (v₂/V₁) = S₂ V₂ LN (v₂/V₁)

Hvis arbeidsstoffet består av m Mol med ideell gass, da kan den ideelle gassligningen påføres: P V = m.R.T.

I dette tilfellet, som P.V₁ = CTTE, en polytropisk prosess med n = 1 er en prosess ved konstant T -temperatur (isotermisk), slik at følgende uttrykk for arbeid kan oppnås:

W = m r t₁ LN (v₂/V₁) = m r t₂ LN (v₂/V₁)

Figur 3. En karamban -smelting, eksempel på isotermisk prosess. Kilde: Pixabay.

Eksempler på polytropiske prosesser

- Eksempel 1

Anta en sylinder med et bevegelig stempel fullt med et kilo luft. Opprinnelig opptar luften et volum V₁= 0,2 m³ Ved et trykk P₁= 400 kPa. En polytropisk prosess følges med n = γ = 1,4, hvis endelige tilstand har trykk P₂ = 100 kPa. Bestem arbeidet som er utført av luften på stempelet.

Løsning

Når polytropiindeksen er lik den adiabatiske konstanten, er det en prosess der arbeidsstoffet (luft) ikke utveksler varme med miljøet, og derfor ikke endrer entropi.

Det kan tjene deg: Tredje lov om termodynamikk: Formler, ligninger, eksempler

For luft, en ideell diatomisk gass, har du:

γ = CP/CV, med CP = (7/2) R og CV = (5/2) R

Så:

γ = 7/5 = 1,4

Ved å bruke uttrykket av den polytropiske prosessen, kan det endelige volumet av luften bestemmes:

V₂ = [S₂ V₁^1.4)/S₂]^(1/1.4) = 0,54 m³.

Nå er det forhold å anvende arbeidsformelen som er gjort i en polytropisk prosess for n ≠ 1 oppnådd ovenfor:

W = (P₂ V₂ - P1 V1)/(1-N)

Erstatte de aktuelle verdiene er:

W = (100 kPa 0,54 m³ - 400 kPa 0,2 m³)/(1 - 1,4) = 65,4 kJ

- Eksempel 2

Anta den samme sylinderen i eksempel 1, med et bevegelig stempel fullt med et kilo luft. Opprinnelig opptar luften et volum V1 = 0,2 m³ ved et trykk P1 = 400 kPa. Men i motsetning til det forrige tilfellet utvider luften isoterisk for å nå et endelig trykk P2 = 100 kPa. Bestem arbeidet som er utført av luften på stempelet.

Løsning

Som tidligere sett, er isotermiske prosesser polytropiske prosesser med indeks n = 1, så det er oppfylt at:

P1 V1 = P2 V2

På denne måten kan det endelige volumet enkelt løsnes for å oppnå:

V2 = 0,8 m³

Deretter bruker du uttrykket av arbeidet som tidligere er oppnådd for saken n = 1, må du jobbe med luften på stempelet i denne prosessen er:

W = p1 v1 ln (v2/v1) = 400000 pa × 0,2 m³ LN (0,8/0,2) = 110,9 kJ.  

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
2. Cengel, og. 2012. Termodynamikk. 7. utgave. McGraw Hill.
3. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 4. Væsker og termodynamikk. Redigert av Douglas Figueroa (USB).
4. López, ca. Den første loven om termodynamikk. Gjenopprettet fra: Culturacientifica.com.
5. Knight, r. 2017. Fysikk for forskere og ingeniørfag: En strategitilnærming. Pearson.
6. Serway, r., Vulle, c. 2011. Fundamentals of Physics. 9na red. Cengage Learning.
7. Sevilla University. Termiske maskiner. Gjenopprettet fra: Laplace.oss.er.
8. Wikiwand. Politropisk prosess. Gjenopprettet fra: wikiwand.com.