Lineær programmering Hva er det for, modeller, begrensninger, applikasjoner

De lineær programmering Det er en matematisk metode som tjener til å optimalisere (maksimere eller minimere etter behov) en funksjon hvis variabler er gjenstand for begrensninger, så lenge funksjonen og begrensningene er lineært avhengig av variablene.

Generelt funksjonen for å optimalisere en praktisk situasjon, for eksempel gevinsten til en produsent hvis innspill, arbeidskraft eller maskiner er begrenset.

Figur 1. Lineær programmering er mye brukt for å optimalisere fortjenesten. Kilde: Piqssels.

En av de enkleste tilfellene er en lineær funksjon å maksimere, som bare avhenger av to variabler, kalt Beslutningsvariabler. Det kan være form:

Z = k₁x + k₂og

Med k₁ og k₂ konstanter. Denne funksjonen er kjent som Objektiv funksjon. Selvfølgelig er det situasjoner som fortjener mer enn to variabler for studien, og er mer komplekse:

Z = k₁x₁ + k₂x₂ + k₃x₃ +.. .

Og begrensninger er også matematisk modellert gjennom et system med ligninger eller ulikninger, like lineære i x og og.

Settet med løsninger av dette systemet kalles gjennomførbare løsninger enten gjennomførbare poeng. Og blant de gjennomførbare punktene er det minst ett, som optimaliserer objektivfunksjonen.

Lineær programmering ble utviklet uavhengig av amerikansk fysiker og matematiker.

Problemløsningsmetoden kjent som Simplex -metode Det er opprettelsen av Dantzig, som jobbet for det amerikanske flyvåpenet, University of Berkeley og Stanford University.

Figur 2. Matematikerne George Dantzig (til venstre) og Leonid Kantorovich (til høyre). Kilde: f. Zapata.

[TOC]

Lineære programmeringsmodeller

De nødvendige elementene for å etablere en lineær programmeringsmodell, som er passende for en praktisk situasjon, er:

-Objektiv funksjon

-Beslutningsvariabler

-Begrensninger

I objektivfunksjonen er det du vil oppnå definert. Anta for eksempel at det er ønsket å maksimere overskuddet som er oppnådd fra fremstilling av visse produkter. Da etableres "fortjeneste" -funksjonen, i henhold til prisen som produktene selges.

I matematiske termer kan denne funksjonen uttrykkes forkortet ved hjelp av summering:

Z = ∑k_Yo x_Yo

I denne ligningen, k_Yo De er koeffisienter og x_Yo er beslutningsvariablene.

Beslutningsvariabler er elementene i systemet hvis kontroll er og deres verdier er positive reelle tall. I det foreslåtte eksemplet er beslutningsvariablene mengden av hvert produkt som skal produseres for å oppnå maksimal forsterkning.

Til slutt har vi begrensningene, som er lineære ligninger eller ulikheter når det gjelder beslutningsvariablene. De beskriver begrensningene for problemet, som er kjent og kan for eksempel være mengden råstoff som er tilgjengelig i produksjon.

Kan tjene deg: funksjoner av høyere enn to (eksempler)

Typer begrensninger

Du kan ha et beløp m begrensninger, fra og med fra og med fra og med start fra J = 1 før J = m. Matematisk er begrensningene av tre typer:

1. TIL_J = ∑ a_ij . x_Yo
2. B_J ≥ ∑ b_ij . x_Yo
3. C_J ≤ ∑ c_ij . x_Yo

Den første begrensningen er av lineær ligningstype og betyr at verdien til_J, som er kjent, må respekteres.

De resterende to begrensningene er lineære ulikninger og betyr at B -verdiene_J og c_J, kjent, kan respekteres eller overvinnes, når symbolet som vises er ≥ (større eller lik) eller respekt eller ikke overvinnes, hvis symbolet er ≤ (mindre enn eller lik).

Modelleksempel

Anvendelsesfeltene er veldig mangfoldige, som dekker fra forretningsadministrasjon til ernæring, men for å forstå metoden foreslås en enkel modell av en praktisk situasjon med to variabler deretter.

Et lokalt kringle er kjent for to spesialiteter: Black Jungle Cake og Sacrista Cake.

I sin utdyping trenger de egg og sukker. For den svarte jungelen er det nødvendig med 9 egg og 500 g sukker, mens 8 egg og 800 g sukker er nødvendig for helligdommen. De respektive salgsprisene er $ 8 og 10.

Problemet er: hvor mange kaker av hver type skal konditoren gjøre for å maksimere gevinsten, vel vitende om at den har 10 kilo sukker og 144 egg?

Beslutningsvariabler

Beslutningsvariablene er "x" og "y", som tar reelle verdier:

-X: Mengden av svarte jungelkaker

-Y: Sacriphantine type kaker.

Begrensninger

Begrensningene er gitt av det faktum at antallet kaker er en positiv mengde og det er begrensede mengder råstoff for å forberede dem.

Derfor, på matematisk måte, skaffer disse begrensningene skjemaet:

1. x ≥ 0
2. og ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 og ≤ 10

Begrensninger 1 og 2 utgjør Ikke -negativitetstilstand Tidligere utsatt, og alle ulikhetene som er hevet er lineære. I begrensninger 3 og 4 er verdiene som ikke bør overvinnes: 144 egg og 10 kg sukker.

Objektiv funksjon

Endelig er den objektive funksjonen forsterkningen oppnådd ved å produsere “x” mengde svarte jungelkaker pluss “y” mengde sakristiner. Den er bygget multipliserer pris med mengde kaker som er laget og legger til for hver type. Det er en lineær funksjon som vi vil kalle G (x, y):

G = 8x + 10y

Løsningsmetoder

Blant de forskjellige løsningsmetodikkene er grafiske metoder, simplex -algoritmen og den indre punktmetoden, for å nevne noen.

- Grafisk eller geometrisk metode

Når du har et problem med to variabler som forrige seksjon, bestemmer begrensningene et polygonalt område i flyet Xy, anrop gjennomførbar region enten Levedyktighetsregion.

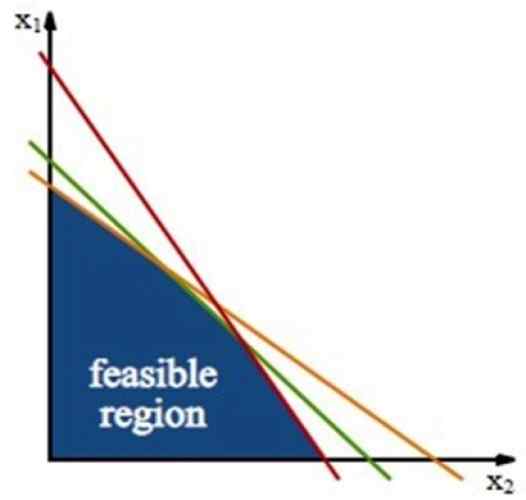Figur 3. Det gjennomførbare området, der løsningen av optimaliseringsproblemet er lokalisert. Kilde: Wikimedia Commons.

Denne regionen er bygget gjennom Begrensningslinjer, som er linjene oppnådd fra ulikhetene av begrensningene, og fungerer bare med tegn på likhet.

Kan tjene deg: endelig sett: egenskaper, eksempler, løste øvelser

Når det gjelder bakeri som ønsker å optimalisere fortjenesten, er restriksjonslinjer:

1. x = 0
2. y = 0
3. 9x +8y = 144
4. 0.5 x + 0.8y = 10

Alle punkter i regionen låst av disse linjene er mulige løsninger, så det er uendelig av dem. Bortsett fra i tilfelle hvor den gjennomførbare regionen er tom, i hvilket tilfelle problemet reiste mangler en løsning.

Heldigvis, for konditorproblemet er det gjennomførbare området ikke tomt, vi har det nedenfor.

Figur 4. Den gjennomførbare regionen i konditorproblemet. Den rette linjen 0 krysser opprinnelsen. Kilde: f. Zapata med Geogebra.

Den optimale løsningen, hvis den eksisterer, er ved hjelp av objektivfunksjonen. Når det for eksempel gjelder å finne maksimal G -forsterkning, har du følgende linje, som kalles ISO-Benefice rett:

G = k₁x + k₂og → y = -k₁x / k₂ + G/ k₂

Med denne linjen oppnås alle par (x, y) som gir en gitt gevinst G, så det er en familie av linjer i henhold til verdien av G, men alle med samme skråning -K₁ / k₂, slik at de er parallelle rett.

Den optimale løsningen

Nå kan det påvises at den optimale løsningen av et lineært problem alltid er en ekstrem eller toppunkt i det gjennomførbare området. Så:

Linjeløsningen er lengst fra opprinnelsen, og som har minst ett poeng til felles med den gjennomførbare regionen.

Hvis linjen nærmest opprinnelsen har et helt segment til felles med den gjennomførbare regionen, sies det at det er uendelige løsninger. Denne saken oppstår hvis skråningen til ISO-fordelene er lik den for noen av de andre linjene som begrenser regionen.

For vårt kringle er kandidathoderen A, B og C.

- Simplex metode for dantzig

Den grafiske eller geometriske metoden gjelder for to variabler. Imidlertid er det mer komplisert når det er tre variabler, og umulig å bruke for et større antall variabler.

Når det gjelder problemer med mer enn to variabler, Simplex -metode, som består av en serie algoritmer for å optimalisere objektive funksjoner. Enkle matriser og aritmetikk brukes vanligvis til å utføre beregningene.

Simplex -metoden begynner med å velge en gjennomførbar løsning og sjekke om den er optimal. Hvis det er vi allerede har løst problemet, men hvis det ikke er det, fortsetter det mot en løsning nærmere optimalisering. Hvis løsningen eksisterer, er algoritmen med den i noen få forsøk.

Kan tjene deg: Hva er statistikkområdet? (Med eksempler)

applikasjoner

Lineær og ikke-lineær programmering brukt på mange felt for å ta de beste beslutningene om å redusere kostnadene og øke fortjenesten, som ikke alltid er monetære, siden de kan måles i tid, for eksempel hvis du søker å minimere det nødvendige tiden for å utføre ut En serie operasjoner.

Her er noen felt:

-I markedsføring brukes det til å finne den beste kombinasjonen av medier (sosiale nettverk, TV, presse og andre) for å annonsere et bestemt produkt.

-For tildeling av arbeid som er passende for personellet til et selskap eller en fabrikk eller planlegger dem.

-I valg av den mest næringsrike maten og til den laveste prisen i husdyr- og fjærkreindustrier.

Løste øvelser

- Oppgave 1

Graf den lineære programmeringsmodellen hevet i de foregående seksjonene.

Løsning

Det er nødvendig å tegne settet med verdier som er bestemt av systemet med begrensninger som er spesifisert i problemet:

1. x ≥ 0
2. og ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 og ≤ 10

Regionen gitt av ulikninger 1 og 2 tilsvarer den første kvadranten av det kartesiske planet. Når det gjelder ulikninger 3 og 4, begynner det med å finne restriksjonslinjene:

9x +8y = 144

0.5 x + 0.8y = 10 → 5x + 8y = 100

Den gjennomførbare regionen er en firkantet hvis toppunkter er punkt A, B, C og D.

Minimumsgevinsten er 0, derfor er 8x + 10 og 10 -linjen den nedre grensen og ISO -fordelingslinjene i påvente av -8/10 = -0.8.

Denne verdien er forskjellig fra skråningene til de andre restriksjonslinjene, og ettersom det gjennomførbare området er begrenset, er det den unike løsningen.

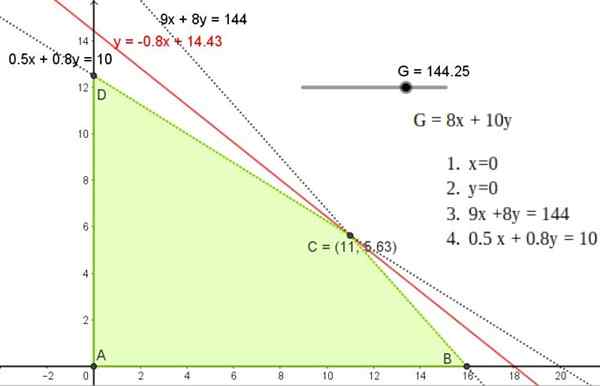Figur 5. Grafisk løsning av trening 1, som viser det gjennomførbare området og punktløsningen C i en av toppunktene i nevnte område. Kilde: f. Zapata.

Denne løsningen tilsvarer en skråningslinje -0.8 som går gjennom et av punktene A, B eller C, hvis koordinater er:

A (11; 5.625)

B (0; 12.5)

C (16, 0)

Optimal løsning

Vi beregner verdien av G for hvert av disse punktene:

-(11; 5.625): g_TIL = 8 x 11 + 10 x 5.625 = 144.25

-(0; 12.5): G_B = 8 x 0 + 10 x 12.5 = 125

-(16, 0): g_C = 8 x 16 + 10 x 0 = 128

Den største gevinsten er å produsere 11 Black Jungle Cakes og 5.625 Sacripantine kaker. Denne løsningen stemmer overens med den som er funnet gjennom programvaren.

- Oppgave 2

Kontroller resultatet av den forrige øvelsen ved å bruke Solver (Solution) -funksjonen som.

Løsning

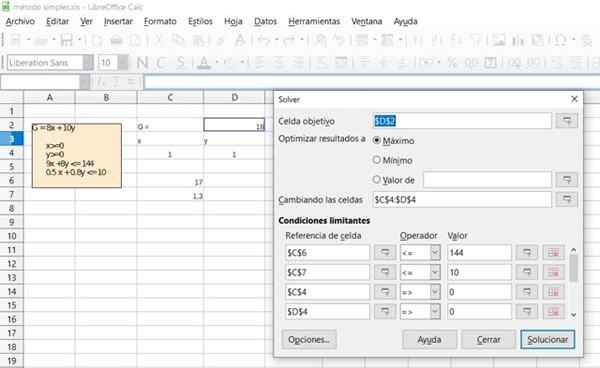Figur 6. Detalj om løsningen av øvelse 1 gjennom det gratis kontoret foralset regneark. Kilde: f. Zapata. 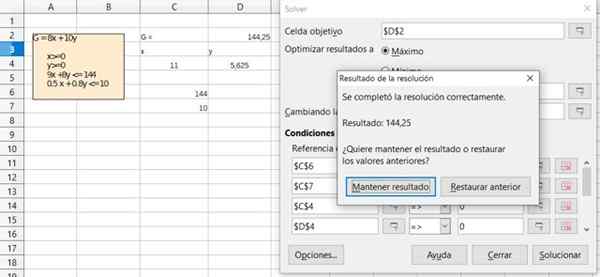Figur 7. Detalj om løsningen av øvelse 1 gjennom det gratis kontoret foralset regneark. Kilde: f. Zapata.

Referanser

1. Strålende. Lineær programmering. Gjenopprettet fra: strålende.org.
2. Eppen, g. 2000. Operasjonsforskning i administrativ vitenskap. 5. plass. Utgave. Prentice Hall.
3. Haeussler, e. 1992. Matematikk for administrasjon og økonomi. 2. Utgave. Ibero -American redaksjonell gruppe.
4. Hiru.Eus. Lineær programmering. Gjenopprettet fra: Hiru.Eus.
5. Wikipedia. Lineær programmering. Gjenopprettet fra: er. Wikipedia.org.