Ikke -lineære programmeringsmetoder og øvelser

De Ikke -lineær programmering Det er prosessen med å optimalisere en funksjon som avhenger av flere uavhengige variabler, som igjen er underlagt begrensninger.

Hvis en eller flere av begrensningene, eller hvis funksjonen skal maksimere eller minimere (kalt Objektiv funksjon), er ikke uttrykt som en lineær kombinasjon av variablene, så det er et ikke -lineært programmeringsproblem.

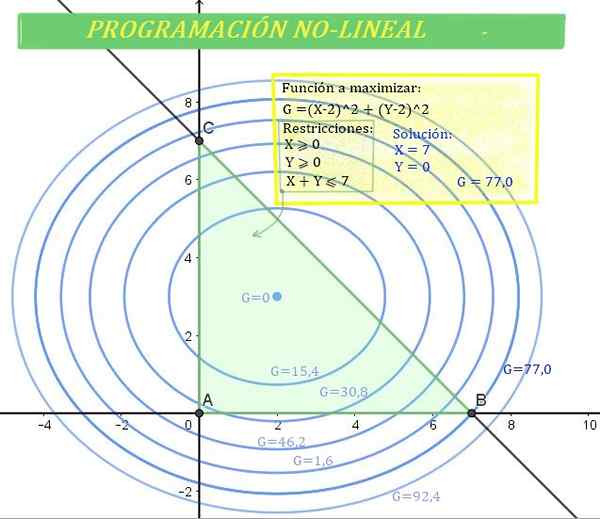
Figur 1. Ikke -lineær programmeringsproblem (NLP). der g er funksjonen (ikke-lineær) for å optimalisere i det grønne området, bestemt av begrensningene. Kilde: f. Zapata.

Og derfor kan ikke prosedyrene og metodene for lineær programmering brukes.

For eksempel kan den velkjente metoden ikke brukes Simplex, som bare gjelder når objektivfunksjonen og begrensningene er alle lineære kombinasjoner av variablene i problemet.

[TOC]

Lineære programmeringsmetoder

For ikke-lineær programmering er hovedmetodene som skal brukes: 

1.- Grafiske metoder.

2.- Lagrange -multiplikatorer for å utforske grensen i løsningsregionen.

3.- Gradientberegning for å utforske ender av objektivfunksjonen.

4.- Den synkende trinnmetoden, for å finne nullgradientpunktene.

5.- Modifisert metode for Lagrange-multiplikatorer (med tilstanden til Karush-Kuhn-Tucker).

Eksempel på løsning med grafisk metode

Et eksempel på en løsning med den grafiske metoden er det som kan sees i figur 2:

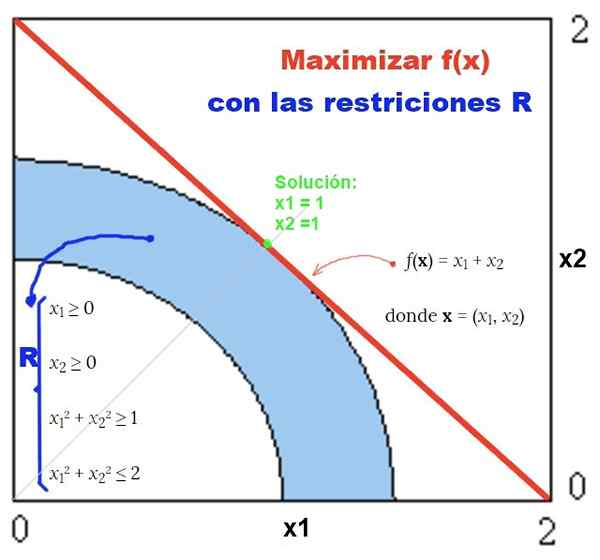Figur 2. Eksempel på ikke-lineært problem med ikke-lineale begrensninger og dens grafiske løsning. Kilde: f. Zapata.

Øvelser

- Oppgave 1 (grafisk metode)

Gevinsten G for et bestemt selskap avhenger av beløpet som er solgt av produkt X og beløpet som selges av produktet, og i tillegg bestemmes forsterkningen av følgende formel:

Kan tjene deg: konjugert binomial: hvordan det løses, eksempler, øvelser

G = 2 (x - 2)² + 3 (og - 3)²

Det er kjent at mengdene X og Y har følgende begrensninger:

X≥0; Y≥0 og x + og ≤ 7

Bestem verdiene til x og y som gir maksimal forsterkning.

Figur 3. Selskapets gevinst kan modelleres matematisk for å finne maksimal gevinst ved ikke -lineær programmering. Kilde: Pixabay.

Løsning 

I dette problemet er objektivfunksjonen ikke -lineær, mens ulikhetene som definerer begrensningene er. Det er et problem med Ikke -lineær programmering.

For løsningen av dette problemet vil den grafiske metoden bli valgt.

For det første vil løsningsregionen bli bestemt, som er gitt av begrensningene.

Som x≥0; Y≥0, løsningen må søke i den første kvadranten av XY -planet, men som i tillegg må den oppfylles at x + y ≤ 7, er løsningen i den nedre semplanen til linjen x + y = 7.

Løsningsregionen er skjæringspunktet mellom den første kvadranten med den nedre semplanen på linjen, noe som gir opphav til et trekantet område der løsningen er lokalisert. Er det samme som indikert i figur 1.

På den annen side kan gevinst G også være representert i det kartesiske planet, siden ligningen er en ellipse med sentrum (2,3).

Ellipsen er vist i figur 1 for flere G -verdier. En høyere verdi av G, større gevinst.

Det er løsninger som tilhører regionen, men ikke gir maksimal verdi G, mens andre, for eksempel G = 92.4, er ute av den grønne sonen, det vil si løsningssonen.

Deretter tilsvarer den maksimale verdien av G, slik at x e y løsningen, oppløsningsregionen: 

Kan tjene deg: Teoretisk sannsynlighet: Hvordan få det ut, eksempler, øvelser

G = 77 (maksimal forsterkning), som oppstår for x = 7 e y = 0. 

Interessant nok oppstår den maksimale gevinsten når mengden produktsalg og er ugyldig, mens mengden produkt x når sin største mulige verdi.

- Oppgave 2 (Analytisk metode: Lagrange Multipliers) 

Finn løsningen (x, y) som gjør funksjonen f (x, y) = x² + 2 og² være maksimal i region g (x, y) = x² + og² - 1 = 0.

Løsning

Det er helt klart et ikke-lineært programmeringsproblem, siden både objektivfunksjonen f (x, y) og begrensningen g (x, y) = 0, ikke er en lineær kombinasjon av variablene x og y.

Lagrange -multiplikatormetoden vil bli brukt, som først krever å definere funksjonen til Lagrange L (x, y, λ):

L (x, y, λ) = f (x, y) - λ g (x, y) = x² + 2 og² - λ (x² + og² - 1) 

Der λ er en parameter som heter Lagrange multiplikator.

For å bestemme de ekstreme verdiene for objektivfunksjonen f, i løsningsområdet gitt av begrensningen g (x, y) = 0, følges disse trinnene:

-Finn de delvise derivater av Lagrange Ls funksjon, med hensyn til x, y, λ.

-Null hvert derivat.

Her sekvensen av disse operasjonene:

1. ∂l/∂x = 2x - 2λx = 0
2. ∂l/∂y = 4y - 2λy = 0
3. ∂l/∂λ = -(x² + og² - 1) = 0

Mulige systemløsninger

En mulig løsning av dette systemet er λ = 1 for å tilfredsstille den første ligningen, i hvilket tilfelle y = 0 for å møte den andre.

Denne løsningen innebærer at x = 1 eller x = -1 slik at den tredje ligningen er fornøyd. På denne måten er det oppnådd to S1- og S2 -løsninger:

S1: (x = 1, y = 0)

S2: (x = -1, y = 0).

Det andre alternativet er at λ = 2 for den andre ligningen som skal være fornøyd, uavhengig av verdien og.

Det kan tjene deg: Fermat Limit: Det som består av øvelser løst

I dette tilfellet er den eneste måten for den første ligningen som skal tilfredsstilles at x = 0. Tatt i betraktning den tredje ligningen, er det bare to mulige løsninger, som vi vil kalle S3 og S4:

S3: (x = 0, y = 1)

S4: (x = 0, y = -1)

For å vite hvilken eller hvilken av disse løsningene som maksimerer objektivfunksjonen, fortsett å erstatte i F (x, y):

S1: F (1, 0) = 1² + 2.0² = 1

S2: F (-1, 0) = (-1)² + 2.0² = 1

S3: F (0, 1) = 0² + 2.1² = 2

S4: F (0, -1) = 0² + tjueen)² = 2

Vi konkluderer med at løsningene som maksimerer f, når x og y tilhører omkretsen g (x, y) = 0 er S3 og S4.

Verdiparene (x = 0, y = 1) y (x = 0, y = -1) maksimer f (x, y) i løsningsområdet g (x, y) = 0.

- Oppgave 3 (nullgradient)

Finn løsninger (x, y) for objektivfunksjonen:

f (x, y) = x² + 2 og²

Være maksimal i region g (x, y) = x² + og² - 1 ≤ 0.

Løsning

Denne øvelsen ligner på oppgave 2, men løsningsregionen (eller begrensningen) strekker seg til det indre området i omkretsen g (x, y) = 0, det vil si til sirkelen g (x, y) ≤ 0. Dette inkluderer omkretsen og dens indre region.

Grenseløsningen var allerede bestemt i oppgave 2, men det er nødvendig å utforske det indre regionen.

For å gjøre dette, må gradienten til funksjonen f (x, y) beregnes og lik null, for å se etter ekstreme verdier i løsningsregionen. Dette tilsvarer å beregne de delvise derivater av f med hensyn til x og henholdsvis og utjevne null:

∂f/∂x = 2 x = 0

∂f/∂y = 4 y = 0

Dette ligningssystemet har den eneste løsningen (x = 0, y = 0) som tilhører sirkel g (x, y) ≤ 0.

Bytte ut denne verdien i funksjon F -resultater:

f (0, 0) = 0

Avslutningsvis er den maksimale verdien som tar funksjonen i løsningsområdet 2 og oppstår på grensen til løsningsregionen, for verdier (x = 0, y = 1) y (x = 0, y = -1).

 Referanser

1. Avriel, m. 2003. Ikke -lineær programmering. Dover Publishing.
2. Bazaraa. 1979. Ikke -lineær programmering. John Wiley & Sons.
3. Bertsekas, d. 1999. Ikke -lineær programmering: 2. utgave. Athena vitenskapelig.
4. Nocedal, J. 1999. Numerisk optimalisering. Springer-Verlag.
5. Wikipedia. Ikke -lineær programmering. Gjenopprettet fra: er.Wikipedia.com