Radikale egenskaper

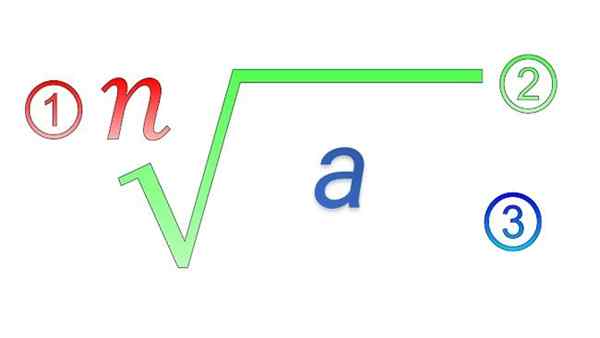Radikale elementer: 1) Indeks; 2) radikalt symbol; 3) Subradisk mengde

Hva er egenskapene til radikaler?

De Radikale egenskaper De er operasjoner som tillater å løse komplekse problemer med radikaler og krefter. Radikalen er måten å symbolisere matematisk til N-EME av et beløp "A". Denne roten er en annen mengde, kalt "B", slik at navnet er nøyaktig "A", så det er gyldig å skrive følgende:

Verdien av "n" er et naturlig tall, som er kjent som rotindeksen, "A" er Radikering eller subradisk mengde, og "b" er n-emet til "en" rot. Både "A" og "B" tilhører settet med reelle tall.

Hvis indeksen ikke er skrevet i en radikal, forstås det umiddelbart at verdien er lik 2 og leser "kvadratrot av a".

Siden "N" tilhører settet med naturlige tall, kan det være et par eller oddetall. Deretter blir følgende tilfeller utmerket:

For "n" par

• Hvis a> 0 eller lik 0, er n-alkalroten til “A” positiv eller 0, og kalles hovedrot.
• Når til < 0, no existe raíz n-ésima en el conjunto de los números reales, pero sí en los números complejos.

For “n” rart

• Ja A> 0, N-EME av “A” -roten er positiv.
• Når til< 0, la raíz n-ésima de “a” es negativa.

Noen eksempler er følgende:

Filmeregenskaper

Det er mulig å skrive navnet på et beløp på et beløp som en kraft med brøkeksponent, det vil si et rasjonelt tall.

I dette tilfellet blir rotindeksen nevneren, mens eksponenten for den subradiske mengden blir telleren:

Kan tjene deg: Homografisk funksjon: Hvordan graf, løste øvelser

Uttrykk som er gyldig så lenge n ≠ 0, siden ingen brøk med en nevner er innrømmet.

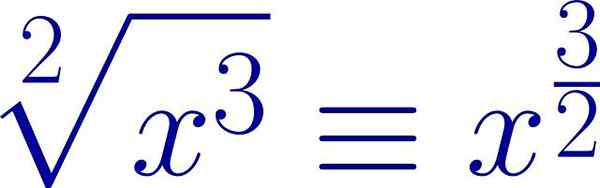Eksempel på et radikalt uttrykk skrevet i form av en brøkeksponent. Rotindeksen er eksponentens nevner, mens sendingen er telleren er telleren. Kilde: Wikimedia Commons.

På denne måten kan de samme egenskapene som gjelder kreftene, brukes i tilfelle av radikaler.

For verdier som tilhører settet med reelle tall, er disse egenskapene som følger:

1. Radikal produkt av lik indeks

I produktet av to (eller flere) radikaler med samme indeks, multipliseres de subradiske mengder multiplisert, og opprettholder indeksen:

2. Radikal kvotient av samme indeks

Kvotienten mellom n-den roten til "A" og n-emen til "B", som er b ≠ 0, er lik n-em-emeasy roten til kvotienten mellom "A" og "B":

3. Rotrot

For å finne den n-emeasy roten til M-EME av beløpet "A", er den subradiske mengden skrevet under en rot hvis indeks er produktet mellom "n" og "m":

Prosedyren utvides lett til påfølgende nestede røtter. Den resulterende rotindeksen er produktet av alle indekser, som dette:

4. Rotkraft

En n-som, hevet til kraften m, uttrykker den subradiske mengden til nevnte makt:

Bestemte tilfeller:

1) Ja n = m, Rottegnet forsvinner, og etterlater basen til kraft 1:

Som er gyldig for ≥ 0. Generelt, hvis rotindeksen er et jevnt tall, har du:

(Se eksempler senere)

2) Ja m> n, M/N -brøkdelen er upassende og roten kan forenkles, for eksempel på jakt etter brøkdelen som tilsvarer M/N slik at telleren og denominatoren er søskenbarn med hverandre, eller omskriver den subradiske mengden og bruker noen av Egenskaper beskrevet her.

Kan tjene deg: Prismer og pyramider

(Se eksempler senere)

5. Radikal forsterkning

En radikal kan forsterkes med en faktor q, Hvis både rotindeksen, så vel som kraften i den subradiske mengden, multipliserer med nevnte faktor, og denne operasjonen ikke innebærer modifisering av resultatet. Derfor:

Forutsatt at a ≥ 0 når det er til og med.

6. Introduksjon av en faktor i en radikal

Hvis en positiv "B" -faktor multipliserer en radikal, kan den passere innenfor den, hvis den stiger til samme rotindeks. I så fall:

7. Sum og subtraksjon av radikaler

Radikalene kan legge til og trekke fra, så lenge de er den samme indeksen og har samme subradiske mengde.

Når to eller flere radikale er av lik indeks og subradisk mengde, sies det at de er Lignende radikaler.

Følgende radikaler er for eksempel like:

I stedet er ikke disse radikaler like, fordi de ikke har den samme subradiske mengden:

Disse to er heller ikke like:

Siden den radikale indeksen ikke er den samme.

Lignende radikaler kan reduseres til en, legge til eller trekke fra koeffisientene som følger dem med dem.

Radikale egenskaper eksempler

Eksempel 1

Hva er verdien av følgende røtter?

Kvadratroten av 32 finner du direkte ved hjelp av kalkulatoren. Verdien er:

Suspensive punkter indikerer at det er uendelig desimal.

Hvis du foretrekker å ikke jobbe med desimaltall, kan kvadratroten til 32 også beregnes ved å nedbryte 32 i de viktigste faktorene:

32 = 2⁵

På denne måten, når den erstatter, oppnås det:

Kan tjene deg: Divisors of 8: Hva er og enkel forklaring

Skrevet som en brøkeksponent:

Fraksjon 5/2 er upassende, så radikalen kan forenkles ved å bruke kreftene til kreftene:

Bruker nå eiendom 1 ovenfor:

Derfor:

For sin del:

Siden (−2)³ = −8.

I følge eiendom 4:

Og til slutt eksisterer ikke kvadratroten av −8 i settet med reelle tall, selv om det i komplekse tall.

Eksempel 2

Gitt følgende operasjon:

Er det mulig å redusere resultatet?

Forutsatt at radikalene er like, er det mulig å redusere dem, men for dette må de ha samme indeks og den samme subradiske mengden. I forrige eksempel ble det sett at:

En analog prosedyre kan brukes til å skrive den første tilsettingen, slik at den subradiske mengden er lik 2:

Denne radikalen ligner på forrige. Når det gjelder kvadratroten av 81, er dette 9, derfor:

Eksempel 3

Hvilke egenskaper er nødvendig for å bruke for å utføre denne operasjonen?

Vi må bruke egenskaper 3 og 5, som er henholdsvis rot av en rot og introduksjon av en radikal verdi. Først gjelder eiendom 5, for å introdusere “X” som er utenfor den innerste roten:

Og nå er uttrykket klart til å bruke eiendom 3, og multiplisere de respektive indeksene for hver radikal:

Referanser

1. Gonzales, d. 2011. Grunnleggende algebra: teori og praksis. 2. Utgave.
2. Haeussler, e. 2012. Forkalkning. 1. Utgave. Pearson.
3. Khan Acadaem. Eksponenter og radikaler. Gjenopprettet fra: Khanacademy.org.
4. Larson, r. 2012. Forkalkning. 8. Utgave. Cengage Learning.
5. Stewart, J. 2007. Matematikk for beregning. 5. plass. Utgave. Cengage Learning.