Sammensatt proporsjonalitet Forklaring, tre sammensatt regel, øvelser

De Kompositt eller flere proporsjonalitet Det er forholdet mellom mer enn to størrelser, der direkte og omvendt proporsjonalitet kan observeres mellom dataene og det ukjente. Det er en mer avansert versjon av enkel proporsjonalitet, selv om teknikkene som brukes i begge prosedyrene er like.

For eksempel, hvis 7 personer er nødvendige for å laste ned 10 tonn varer på 3 timer, kan den sammensatte proporsjonaliteten brukes til å beregne hvor mange som vil være nødvendige for å laste ned 15 tonn på 4 timer.

Kilde: Pixabay.com

For å svare på dette spørsmålet er det praktisk å lage en tabell med verdier for å studere og relatere størrelser og ukjente.

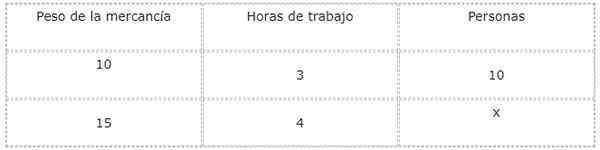
Typene forhold mellom hver størrelse og den nåværende ukjente blir analysert, noe som i dette tilfellet tilsvarer antall mennesker som vil jobbe.

Når vekten av varene øker, øker antallet mennesker som trengs for å laste ned også. På grunn av dette er forholdet mellom vekt og arbeidere direkte.

På den annen side, ved å øke antall arbeidere, reduseres arbeidstiden. På grunn av dette er forholdet mellom mennesker og arbeidstid omvendt.

[TOC]

Hvordan beregne sammensatte proporsjoner

For å løse eksempler som den forrige, brukes de tre sammensatte regelsemetoden for det meste. Dette består i å etablere hvilke typer forhold mellom størrelser og ukjente og deretter representere et produkt mellom brøk.

Når det gjelder det første eksemplet, er brøkene som tilsvarer verdiene organisert som følger:

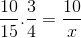
Men før du løser og rydder de ukjente, må brøkene som tilsvarer det omvendte forholdet reverseres. At for dette tilfellet tilsvarer tidsvariabelen. På denne måten vil operasjonen som skal løses være:

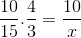
Hvis eneste forskjell er investeringen av brøkdelen som tilsvarer variabel tid 4/3. Verdien av x drives og klar.

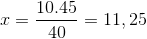
Dermed er det behov for mer enn elleve personer for å laste ned 15 tonn varer på 4 timer eller mindre.

Forklaring

Proporsjonalitet er det konstante forholdet mellom størrelser som er utsatt for endringer, noe som vil være symmetrisk for hver av størrelsene som er involvert. Det er direkte og omvendt proporsjonale forhold, og definerer dermed parametrene til enkel eller sammensatt proporsjonalitet.

Direkte tre regel

Den består av et forhold mellom variabler, som har samme oppførsel når de er endret. Det er veldig hyppig i beregningen av prosentandeler relatert til forskjellige størrelser på hundre, der dens grunnleggende struktur blir verdsatt.

Som et eksempel kan du beregne 15% av 63. Ved første øyekast, sa prosentandel ikke kan sees på en enkel måte. Men implementering av regelen om tre du kan gjøre følgende forhold: Hvis 100% er 63, så 15%, hvor mye vil det være?

Kan tjene deg: Faktor teorem: forklaring, eksempler, øvelser

100%-63

15%-x

Og den tilsvarende operasjonen er:

(femten% . 63) / 100% = 9,45

Der prosentvis tegn er forenklet og 9,45 -tallet som representerer 15% av 63 oppnås.

Tre omvendt regel

Som navnet tilsier, er i dette tilfellet forholdet mellom variablene motsatt. Det omvendte forholdet må etableres før du fortsetter til beregning. Hans prosedyre er homolog med de tre direkte regelen, med unntak av investeringer i brøkdelen som skal beregnes.

For eksempel trenger 3 malere 5 timer for å fullføre en vegg. Hvor mange timer ville 4 malere fullføre?

I dette tilfellet er forholdet omvendt, siden arbeidstiden ved å øke antallet malere skal avta. Forholdet er etablert;

3 malere - 5 timer

4 malere- x timer

Når forholdet er omvendt, blir driftsrekkefølgen reversert. Dette er riktig måte;

(3 malere) . (5 timer) / 4 malere = 3,75 timer

Begrepet malere er forenklet, og resultatet er 3,75 timer.

Betingelse

For å være i nærvær av en forbindelse eller flere proporsjonalitet, er det nødvendig å finne begge typer forhold mellom størrelser og variabler.

- Direkte: Variabelen presenterer samme oppførsel som det ukjente. Det vil si ved å øke eller redusere den ene, blir den andre likt.

- Inverse: Variabelen presenterer en antonymatferd til det av det ukjente. Brøkdelen som definerer denne variabelen i tabellen med verdier, må reverseres, for å representere det omvendt proporsjonale forholdet mellom variabel og ukjent.

Verifisering av resultater

Det er veldig vanlig å forveksle størrelsesorden når du arbeider med sammensatte proporsjoner, i motsetning til hva som skjer i de vanlige proporsjonsberegningene, hvis natur stort sett er direkte og oppløselig ved hjelp av en enkel tre regel.

Derfor er det viktig å undersøke resultatens logiske rekkefølge, og verifisere sammenhengen av figurene som blir kastet av de tre sammensatte regelen.

I det første eksemplet ville det å gjøre denne feilen innebære å skaffe 20 som et resultat. Det vil si at 20 personer for å laste ned 15 tonn varer på 4 timer.

Ved første øyekast virker det ikke som et vanvittig resultat, men en økning på nesten 200% i ansatte (fra 7 til 20 personer) er nysgjerrig når økningen i varer er 50%, og selv med større tid til å utføre arbeid.

Det kan tjene deg: Generell parabola -ligning (eksempler og øvelser)

På denne måten representerer den logiske verifiseringen av resultatene et viktig trinn ved å implementere de tre sammensatte regelen.

Klarering

Selv om av en mer grunnleggende karakter angående matematisk dannelse, representerer klaring et viktig trinn i tilfeller av proporsjonalitet. En feilaktig klarering er tilstrekkelig til å ugyldiggjøre ethvert resultat oppnådd i rekkefølge av tre enkle eller sammensatte.

Historie

Regelen om tre ble kjent i Vesten gjennom araberne, med publikasjoner av flere forfattere. Blant dem al-Jwarizmi og al-Biruni.

Al-Biruni, takket være sin flerkulturelle kunnskap, hadde tilgang til enorm informasjon om denne praksisen i hans turer til India, og var ansvarlig for den mest omfattende dokumentasjonen om de tre reglene for tre.

Det reiser i etterforskningen hans, at India var det første stedet der bruken av de tre reglene ble gjort vanlig. Forfatteren forsikrer at den ble gjort flytende i sine direkte, inverse og til og med komponerte versjoner.

Den nøyaktige datoen som de tre regler ble en del av den matematiske kunnskapen om India er fremdeles ukjent. Imidlertid ble det eldste dokumentet rettet mot denne praksisen, Bakhshalis manuskript, oppdaget i 1881. Det er for tiden i Oxford.

Mange matematikkhistorikere sikrer at dette manuskriptet stammer fra begynnelsen av den nåværende tiden.

Løste øvelser

Oppgave 1

Et flyselskap må flytte 1535 personer. Det er kjent at det med 3 fly vil ta 12 dager å ta til den siste passasjeren til destinasjon. 450 flere mennesker har nådd flyselskapet og to fly blir beordret til å samarbeide med denne oppgaven. Hvor mange dager vil flyselskapet ta til den siste passasjeren til sin destinasjon?

Forholdet mellom antall mennesker og arbeidsdager er direkte, fordi jo flere mennesker, flere dager vil bli pålagt å utføre dette arbeidet.

På den annen side er forholdet mellom fly og dager omvendt proporsjonalt. Ved å øke mengden fly, reduseres de nødvendige dagene for å overføre til alle passasjerer.

Verdiene som refererer til denne saken blir utført.

Som beskrevet i det første eksemplet, må teller og nevner må investeres i brøkdelen som tilsvarer den omvendte variabelen med hensyn til det ukjente. Forlater operasjonen som følger:

Kan tjene deg: beregning av tilnærminger ved bruk av differensialer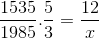

X = 71460/7675 = 9,31 dager

For å flytte til 1985 personer som bruker 5 fly, er mer enn 9 dager nødvendig.

Oppgave 2

En 25 -tonn maishøst blir tatt til lastebiler. Det er kjent at året før tok 8 timer med en lønn på 150 arbeidere. Hvis lønningslisten i år øker 35%, hvor lang tid vil det ta å fylle lastbilene med en høsting av 40 -tonn?

Før du representerer verdiene, må antallet arbeidere for dette året defineres. Dette økte 35% av det første tallet på 150 arbeidere. For dette brukes en direkte tre regel.

100% - 150

35% - x

X = (35 . 100)/100 = 52,5. Dette er antall ekstra arbeidere med hensyn til året før, og skaffer seg et totalt antall 203 arbeidere, ulykkelig for å runde beløpet som er oppnådd.

Den tilsvarende datatabellen er definert

For dette tilfellet representerer vekten en direkte forholdsvariabel med den ukjente tiden. På den annen side klarer arbeidernes variabel et omvendt forhold til tiden. Et større antall arbeidere, dagen vil være kortere.

Å ta hensyn til disse hensynene og investere brøkdelen som tilsvarer arbeiderne, beregnes den.

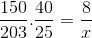
X = 40600 /6000 = 6,76 timer

Dagen vil ta litt mindre enn 7 timer.

Foreslåtte øvelser

- Definer 73% av 2875.

- Beregn mengden timer Teresa sover, hvis det er kjent at bare 7% av totalen av dagen sover. Definer hvor mange timer sover i uken.

- En offentlig avis fra 2000 hver 5. time, med bare 2 utskriftsmaskiner. Hvor mange eksemplarer vil produsere på 1 time, hvis du bruker 7 maskiner? Hvor lenge vil produsere 10.000 eksemplarer ved hjelp av 4 maskiner?

Referanser

1. Encyclopedia Alvarez-Iniciacion. TIL. Álvarez, Antonio Álvarez Pérez. Edaf, 2001.
2. Komplett elementær og overlegen primær bruksanvisning: For bruk av søkere til lærere og spesielt elevene ved normale provinsskoler, bind 1. Joaquín Avendaño. Utskrift d. Dionisio Hidalgo, 1844.
3. Vurdering tilnærming av reelle funksjoner. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. mars. 2011.
4. Elementær aritmetikk for undervisning på skoler og skoler i Mellom -Amerika. Darío González. Tips. Arenales, 1926.
5. Studien av matematikk: På studien og matematikkens studier og vanskeligheter. Augustus de Morgan. Baldwin og Cradock, 1830.